ГДЗ по Алгебре 7 Класс Вариант 1 Домашняя Контрольная Работа 8 Номер 10 Мордкович — Подробные Ответы

Постройте график функции

y = (2x² — x³):(x — 2) = (-x²(x — 2)):(x — 2) = -x², x ≠ 2

Рассмотрим функцию:

\[
y = \frac{2x^2 — x^3}{x — 2}.
\]

Шаг 1. Упрощение числителя

Вынесем общий множитель из числителя:
\[
2x^2 — x^3 = x^2(2 — x) = -x^2(x — 2).
\]

Таким образом, исходное выражение принимает вид:
\[
y = \frac{-x^2(x — 2)}{x — 2}.
\]

Шаг 2. Сокращение дроби

При условии, что \(x — 2 \ne 0\) (то есть \(x \ne 2\)), можно сократить числитель и знаменатель на общий множитель \(x — 2\):
\[
y = -x^2, \quad x \ne 2.
\]

Шаг 3. Анализ области определения

Исходная функция не определена при \(x = 2\), так как знаменатель обращается в ноль. После сокращения получается функция \(y = -x^2\), которая сама по себе определена для всех действительных чисел. Однако **область определения исходной функции остаётся ограниченной**: \(x = 2\) исключается.

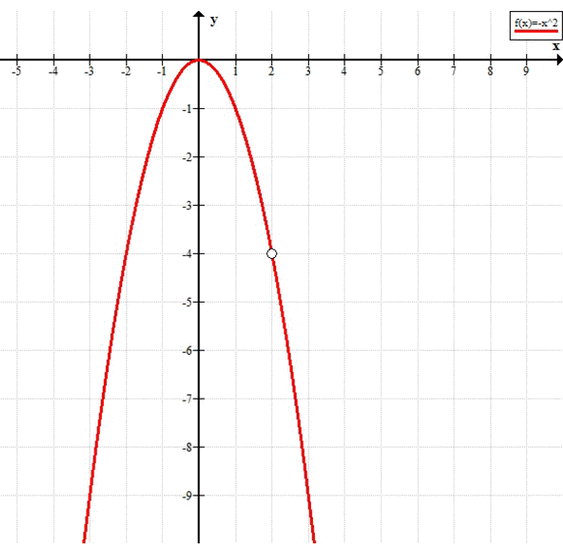
Следовательно, график функции совпадает с параболой \(y = -x^2\), но с одной «выколотой» точкой в месте \(x = 2\).

Шаг 4. Координаты выколотой точки

Подставим \(x = 2\) в упрощённое выражение, чтобы найти, какой точки не хватает на графике:
\[
y = -(2)^2 = -4.
\]

Таким образом, на графике параболы \(y = -x^2\) отсутствует точка с координатами \((2; -4)\).

Шаг 5. Итоговое описание функции

Функция эквивалентна квадратичной функции \(y = -x^2\) на всей числовой прямой, за исключением точки \(x = 2\). Это означает, что:
— область определения: \((-\infty; 2) \cup (2; +\infty)\),
— множество значений: \((-\infty; 0]\) (поскольку \(y = -x^2 \leq 0\)),
— функция чётная на своей области определения,
— график — парабола, ветви которой направлены вниз, с «дыркой» в точке \((2; -4)\).

Такое поведение типично для рациональных функций, где после сокращения общего множителя остаётся устранимый разрыв.