ГДЗ по Алгебре 7 Класс Вариант 1 Домашняя Контрольная Работа 8 Номер 2 Мордкович — Подробные Ответы

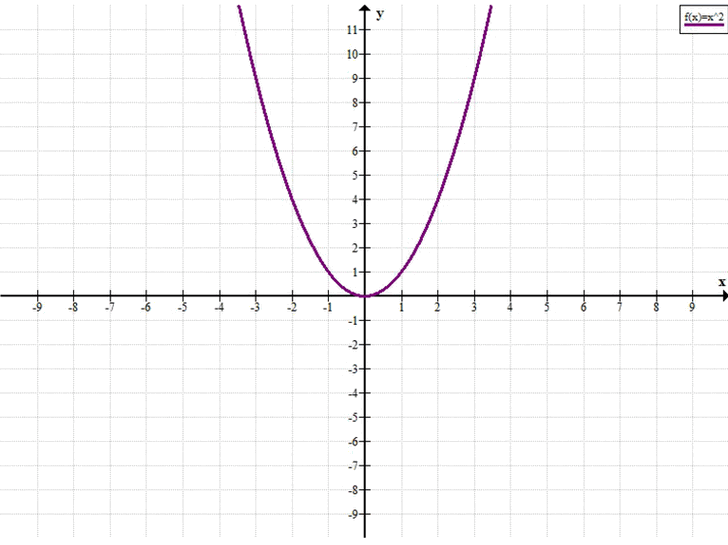
Постройте график функции у = x² и с его помощью найдите наименьшее и наибольшее значения функции на заданном промежутке: а) [-2; 3]; б) (-3; 1]; в) (-бесконечность; -1].

а)
График функции  \(y = x^2\)  — это парабола, ветви которой направлены вверх, а вершина находится в точке  (0, 0).
\( \text{Рассмотрим промежуток } [-2; 3]. \)
\( \text{Вершина параболы } x = 0 \text{ находится внутри данного промежутка.} \)
\( \text{Наименьшее значение функции достигается в вершине параболы.} \)
\( y_{min} = f(0) = 0^2 = 0 \)
Наибольшее значение функции на замкнутом промежутке достигается на одном из его концов.
\( \text{Сравним значения функции на концах промежутка:} \)
\( f(-2) = (-2)^2 = 4 \)
\( f(3) = 3^2 = 9 \)
\( \text{Наибольшее значение функции на промежутке } [-2; 3] \text{ равно } 9. \)
Ответ: Наименьшее значение: 0, Наибольшее значение: 9

б)
График функции  \(y = x^2\) — это парабола, ветви которой направлены вверх, а вершина находится в точке  (0, 0).
\( \text{Рассмотрим промежуток } (-3; 1]. \)
\( \text{Вершина параболы } x = 0 \text{ находится внутри данного промежутка.} \)
\( \text{Наименьшее значение функции достигается в вершине параболы.} \)
\( y_{min} = f(0) = 0^2 = 0 \)
Для нахождения наибольшего значения рассмотрим поведение функции на концах промежутка.
\( \text{На правом конце промежутка } x = 1, \text{ значение функции } f(1) = 1^2 = 1. \)
\( \text{На левом конце промежутка } x \to -3, \text{ но } x = -3 \text{ не входит в промежуток.} \)
По мере приближения  x  к  -3  (справа), значение функции f(x)  приближается к } (-3)^2 = 9.
\( \text{Так как } x = -3 \text{ не входит в промежуток, функция никогда не достигает значения } 9. \)
\( \text{Следовательно, наибольшего значения на промежутке } (-3; 1] \text{ не существует.} \)
Ответ: Наименьшее значение: 0, Наибольшего значения не существует

в)
График функции  \(y = x^2\)  — это парабола, ветви которой направлены вверх, а вершина находится в точке } (0, 0).
\( \text{Рассмотрим промежуток } (-\infty; -1]. \)
\( \text{Вершина параболы } x = 0 \text{ не находится внутри данного промежутка.} \)
\( \text{На промежутке } (-\infty; 0) \text{ функция } y = x^2 \text{ убывает.} \)
\( \text{Промежуток } (-\infty; -1] \text{ является частью промежутка убывания.} \)
Наименьшее значение функции на этом промежутке достигается на правом конце, так как функция убывает.
\( y_{min} = f(-1) = (-1)^2 = 1 \)
\( \text{Для нахождения наибольшего значения рассмотрим поведение функции при } x \to -\infty. \)
\( \text{По мере того как } x \to -\infty, \text{ значение функции } y = x^2 \to +\infty. \)
\( \text{Следовательно, наибольшего значения на промежутке } (-\infty; -1] \text{ не существует.} \)
Ответ: Наименьшее значение: 1, Наибольшего значения не существует

Условие: Постройте график функции \(у = х^2\) и с его помощью найдите наименьшее и наибольшее значения функции на заданном промежутке:

а)
\( [-2; 3] \);

б)
\( (-3; 1] \);

в)
\( (-\infty; -1] \).

Решение:
Графиком функции \( y = x^2 \) является парабола, ветви которой направлены вверх, а вершина находится в начале координат \( (0,0) \).
Функция убывает на промежутке \( (-\infty; 0] \) и возрастает на промежутке \( [0; +\infty) \).
Наименьшее значение функции равно \( 0 \) и достигается в точке \( x = 0 \).

а) Промежуток \( [-2; 3] \).
Данный промежуток содержит вершину параболы \( x = 0 \).
Следовательно, наименьшее значение функции на этом промежутке достигается в вершине.
\( y_{min} = y(0) = 0^2 = 0 \)
Наибольшее значение функции на данном промежутке достигается на одном из его концов, так как функция возрастает от \( x=0 \) до \( x=3 \) и убывает от \( x=-2 \) до \( x=0 \).
Сравним значения функции на концах промежутка:
\( y(-2) = (-2)^2 = 4 \)
\( y(3) = 3^2 = 9 \)
Наибольшее значение функции на промежутке \( [-2; 3] \) равно \( 9 \).

б) Промежуток \( (-3; 1] \).
Данный промежуток содержит вершину параболы \( x = 0 \).
Следовательно, наименьшее значение функции на этом промежутке достигается в вершине.
\( y_{min} = y(0) = 0^2 = 0 \)
Для нахождения наибольшего значения рассмотрим поведение функции на концах промежутка.
На правом конце промежутка \( x = 1 \):
\( y(1) = 1^2 = 1 \)
На левом конце промежутка \( x = -3 \) не включен в промежуток.
При приближении \( x \) к \( -3 \) справа, значение функции стремится к \( (-3)^2 = 9 \).
Поскольку точка \( x = -3 \) не принадлежит промежутку, значение \( 9 \) не достигается.
Следовательно, наибольшего значения на промежутке \( (-3; 1] \) не существует.

в) Промежуток \( (-\infty; -1] \).
Данный промежуток не содержит вершину параболы \( x = 0 \).
Весь промежуток \( (-\infty; -1] \) находится в области убывания функции \( y = x^2 \).
По мере уменьшения \( x \) (стремления к \( -\infty \)), значение функции \( y \) возрастает до \( +\infty \).
Следовательно, наименьшего значения на промежутке \( (-\infty; -1] \) не существует.
Наибольшее значение функции на этом промежутке достигается на его правом конце, так как функция убывает на этом промежутке.
\( y_{max} = y(-1) = (-1)^2 = 1 \)

Ответы:
а) Наименьшее значение: \( 0 \), наибольшее значение: \( 9 \).
б) Наименьшее значение: \( 0 \), наибольшего значения не существует.
в) Наименьшего значения не существует, наибольшее значение: \( 1 \).