Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Вариант 1 Домашняя Контрольная Работа 8 Номер 5 Мордкович — Подробные Ответы
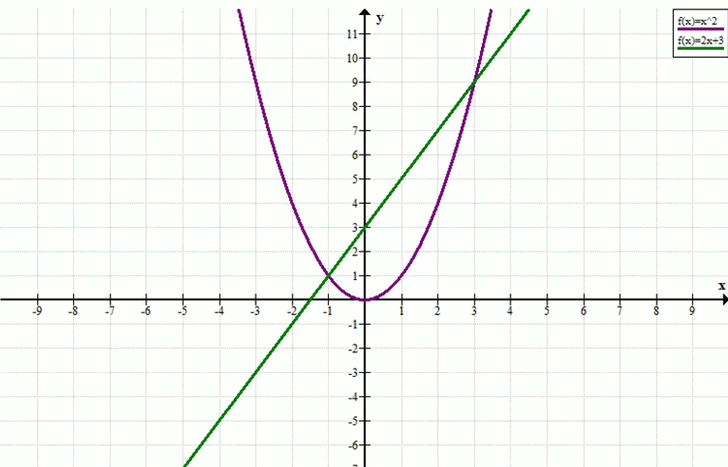
Решите графически уравнение x² = 2х + 3.
\( y = x^2 \)
\( y = 2x + 3 \)
Решением уравнения являются абсциссы точек пересечения графиков функций \( y = x^2 \) и \( y = 2x + 3 \).
Для нахождения точек пересечения приравняем правые части уравнений:
\( x^2 = 2x + 3 \)
\( x^2 — 2x — 3 = 0 \)
\( (x — 3)(x + 1) = 0 \)
\( x — 3 = 0 \)
\( x = 3 \)
\( x + 1 = 0 \)
\( x = -1 \)
Ответ: -1; 3
Условие: Решить графически уравнение \( x^2 = 2x + 3 \)
Решение:
1. Представим данное уравнение в виде системы двух функций:
\( y = x^2 \)
\( y = 2x + 3 \)
2. Построим график функции \( y = x^2 \). Это парабола, вершина которой находится в начале координат \( (0; 0) \).
Для построения параболы найдем несколько точек:
При \( x = 0, y = 0^2 = 0 \)
При \( x = 1, y = 1^2 = 1 \)
При \( x = -1, y = (-1)^2 = 1 \)
При \( x = 2, y = 2^2 = 4 \)
При \( x = -2, y = (-2)^2 = 4 \)
При \( x = 3, y = 3^2 = 9 \)
3. Построим график функции \( y = 2x + 3 \). Это прямая линия.
Для построения прямой найдем две точки:
При \( x = 0, y = 2(0) + 3 = 3 \)
При \( x = -1, y = 2(-1) + 3 = 1 \)
При \( x = 3, y = 2(3) + 3 = 9 \)
4. Найдем точки пересечения графиков функций \( y = x^2 \) и \( y = 2x + 3 \).
Из построенных точек видно, что графики пересекаются в точках \( (-1; 1) \) и \( (3; 9) \).
5. Значения \( x \) в точках пересечения являются решениями исходного уравнения.
Таким образом, решениями уравнения являются \( x = -1 \) и \( x = 3 \).
Ответ: -1; 3