ГДЗ по Алгебре 7 Класс Вариант 1 Домашняя Контрольная Работа 8 Номер 9 Мордкович — Подробные Ответы

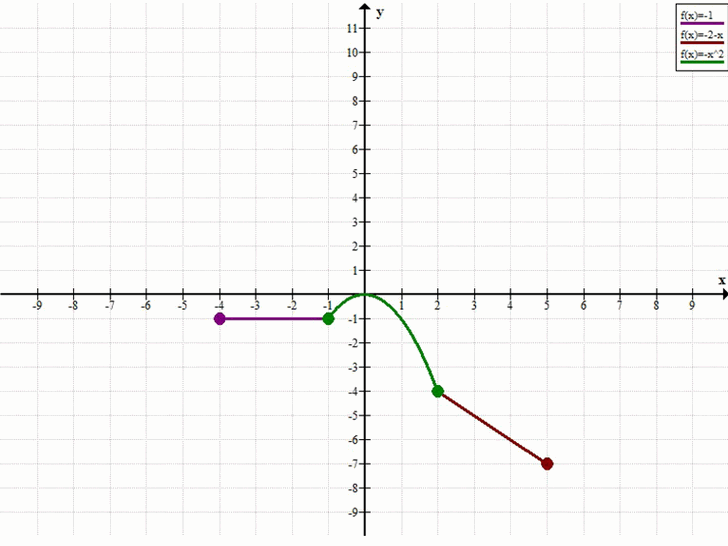
Постройте график функции у = f(x), где f(x) = система -1, если -4 ≤ x < -1; -x², если -1 ≤ х ≤ 2; -2 — x, если 2 < x ≤ 5. Используя построенный график функций, установите: а) какова область определения функции \(у = f(x)\); б) чему равны наименьшее и наибольшее значения функции; в) является ли функция непрерывной; г) при каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля; д) где функция возрастает, где убывает.

а)
\( D(f) = [-4, 5] \)

Ответ: \( [-4, 5] \)

б)
\( \max f(x) = 0 \)
\( \min f(x) = -7 \)

Ответ: \( \max f(x) = 0 \), \( \min f(x) = -7 \)

в) Функция непрерывна.

Ответ: Функция непрерывна

г)
\( f(x) = 0 \Rightarrow x = 0 \)
\( f(x) > 0 \Rightarrow \text{нет решений} \)
\( f(x) < 0 \Rightarrow x \in [-4, 0) \cup (0, 5] \)

Ответ: \( f(x) = 0 \) при \( x = 0 \); \( f(x) > 0 \) нет решений; \( f(x) < 0 \) при \( x \in [-4, 0) \cup (0, 5] \)

д) Возрастает на \( [-1, 0) \)
Убывает на \( (0, 5] \)
Постоянна на \( [-4, -1) \)

Ответ: Возрастает на \( [-1, 0) \); Убывает на \( (0, 5] \); Постоянна на \( [-4, -1) \)

Условие: Постройте график функции \(у = f(x), где f(x) = \begin{cases} -1, & \text{если } -4 \le x < -1 \\ -x^2, & \text{если } -1 \le x \le 2 \\ -2 — x, & \text{если } 2 < x \le 5 \end{cases}\). Используя построенный график функций, установите:

а) какова область определения функции \(у = f(x)\);

б) чему равны наименьшее и наибольшее значения функции;

в) является ли функция непрерывной;

г) при каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля;

д) где функция возрастает, где убывает.

Решение:
Для построения графика функции рассмотрим каждый участок отдельно:

1. Первый участок: \( f(x) = -1 \) при \( -4 \le x < -1 \).
Это горизонтальный отрезок прямой на уровне \( y = -1 \). Левая точка \((-4, -1)\) включена, правая точка \((-1, -1)\) не включена.

2. Второй участок: \( f(x) = -x^2 \) при \( -1 \le x \le 2 \).
Это часть параболы, ветви которой направлены вниз.
При \( x = -1 \), \( f(-1) = -(-1)^2 = -1 \). Точка \((-1, -1)\) включена.
При \( x = 0 \), \( f(0) = -(0)^2 = 0 \). Точка \((0, 0)\) включена.
При \( x = 1 \), \( f(1) = -(1)^2 = -1 \). Точка \((1, -1)\) включена.
При \( x = 2 \), \( f(2) = -(2)^2 = -4 \). Точка \((2, -4)\) включена.

3. Третий участок: \( f(x) = -2 — x \) при \( 2 < x \le 5 \).
Это часть прямой линии.
При \( x \to 2^+ \), \( f(x) \to -2 — 2 = -4 \). Точка \((2, -4)\) не включена (открытый кружок).
При \( x = 5 \), \( f(5) = -2 — 5 = -7 \). Точка \((5, -7)\) включена.

Теперь ответим на вопросы, используя анализ функции и ее графика:

а) Область определения функции \(у = f(x)\):
Область определения функции задается объединением интервалов, на которых определены ее части.
\( D(f) = [-4, -1) \cup [-1, 2] \cup (2, 5] \)
Объединяя эти интервалы, получаем:
\( D(f) = [-4, 5] \)

б) Наименьшее и наибольшее значения функции:
Рассмотрим значения функции на каждом участке:
На первом участке \( f(x) = -1 \).
На втором участке \( f(x) = -x^2 \). Максимальное значение \( 0 \) при \( x = 0 \), минимальное значение \( -4 \) при \( x = 2 \).
На третьем участке \( f(x) = -2 — x \). Функция убывает. Значения изменяются от \( -4 \) (не включая) до \( -7 \) (включая).
Сравнивая все значения: \( -1, 0, -4, -7 \).
Наибольшее значение функции равно \( 0 \) (достигается при \( x = 0 \)).
Наименьшее значение функции равно \( -7 \) (достигается при \( x = 5 \)).

в) Является ли функция непрерывной:
Проверим непрерывность в точках «стыковки» интервалов: \( x = -1 \) и \( x = 2 \).
В точке \( x = -1 \):
\( \lim_{x \to -1^-} f(x) = -1 \) (из первого участк

а)
\( f(-1) = -(-1)^2 = -1 \) (из второго участк

а)
\( \lim_{x \to -1^+} f(x) = -(-1)^2 = -1 \) (из второго участк

а)
Так как \( \lim_{x \to -1^-} f(x) = f(-1) = \lim_{x \to -1^+} f(x) \), функция непрерывна в \( x = -1 \).

В точке \( x = 2 \):
\( \lim_{x \to 2^-} f(x) = -(2)^2 = -4 \) (из второго участк

а)
\( f(2) = -(2)^2 = -4 \) (из второго участк

а)
\( \lim_{x \to 2^+} f(x) = -2 — 2 = -4 \) (из третьего участк

а)
Так как \( \lim_{x \to 2^-} f(x) = f(2) = \lim_{x \to 2^+} f(x) \), функция непрерывна в \( x = 2 \).
Каждый из кусочных участков является непрерывной функцией на своем интервале. Поскольку функция непрерывна в точках стыковки, она непрерывна на всей своей области определения.

г) При каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля:
1. Значение функции равно нулю (\( f(x) = 0 \)):
На первом участке \( -1 = 0 \) (нет решений).
На втором участке \( -x^2 = 0 > x = 0 \). Это значение входит в интервал \( [-1, 2] \).
На третьем участке \( -2 — x = 0 > x = -2 \). Это значение не входит в интервал \( (2, 5] \).
Таким образом, \( f(x) = 0 \) при \( x = 0 \).

2. Значение функции больше нуля (\( f(x) > 0 \)):
На первом участке \( -1 > 0 \) (нет решений).
На втором участке \( -x^2 > 0 \). Поскольку \( x^2 \ge 0 \), то \( -x^2 \le 0 \). Значит, \( -x^2 > 0 \) не имеет решений.
На третьем участке \( -2 — x > 0 > -x > 2 > x < -2 \). Это значение не входит в интервал \( (2, 5] \).
Таким образом, \( f(x) > 0 \) не имеет решений.

3. Значение функции меньше нуля (\( f(x) < 0 \)):
На первом участке \( -1 < 0 \) для всех \( x \in [-4, -1) \).
На втором участке \( -x^2 < 0 \) для всех \( x \in [-1, 2] \), кроме \( x = 0 \). То есть для \( x \in [-1, 0) \cup (0, 2] \).
На третьем участке \( -2 — x < 0 > -x < 2 > x > -2 \). Это условие выполняется для всех \( x \in (2, 5] \).
Объединяя эти интервалы: \( x \in [-4, -1) \cup [-1, 0) \cup (0, 2] \cup (2, 5] \).
Это упрощается до \( x \in [-4, 0) \cup (0, 5] \).

д) Где функция возрастает, где убывает:
1. На первом участке \( f(x) = -1 \) при \( -4 \le x < -1 \). Функция постоянна.
2. На втором участке \( f(x) = -x^2 \) при \( -1 \le x \le 2 \).
Производная \( f'(x) = -2x \).
\( f'(x) > 0 \) при \( -2x > 0 > x < 0 \). Функция возрастает на \( [-1, 0) \).
\( f'(x) < 0 \) при \( -2x < 0 > x > 0 \). Функция убывает на \( (0, 2] \).
3. На третьем участке \( f(x) = -2 — x \) при \( 2 < x \le 5 \).
Производная \( f'(x) = -1 \).
\( f'(x) < 0 \) для всех \( x \) в интервале. Функция убывает на \( (2, 5] \).

Итого:
Функция возрастает на интервале \( [-1, 0) \).
Функция убывает на интервале \( (0, 2] \cup (2, 5] \), что можно записать как \( (0, 5] \) ввиду непрерывности в \( x=2 \).
Функция постоянна на интервале \( [-4, -1) \).

Ответы:
а) Область определения функции: \( [-4, 5] \)
б) Наименьшее значение функции: \( -7 \), наибольшее значение функции: \( 0 \)
в) Функция является непрерывной.
г) Значение функции равно нулю при \( x = 0 \).
Значение функции больше нуля: нет таких значений аргумента.
Значение функции меньше нуля при \( x \in [-4, 0) \cup (0, 5] \).
д) Функция возрастает на \( [-1, 0) \).
Функция убывает на \( (0, 5] \).
Функция постоянна на \( [-4, -1) \).