Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Вариант 2 Домашняя Контрольная Работа 3 Номер 2 Мордкович — Подробные Ответы
Решите графически систему уравнений система 3x + у = 2, х — 2у = 3.
1)
\( 3x + y = 2 \)
\( y = -3x + 2 \)
\( x — 2y = 3 \)
\( x — 3 = 2y \)
\( y = \frac{1}{2}x — \frac{3}{2} \)
\( -3x + 2 = \frac{1}{2}x — \frac{3}{2} \)
\( 2 + \frac{3}{2} = \frac{1}{2}x + 3x \)
\( \frac{4}{2} + \frac{3}{2} = \frac{1}{2}x + \frac{6}{2}x \)
\( \frac{7}{2} = \frac{7}{2}x \)
\( x = 1 \)
\( y = -3(1) + 2 \)
\( y = -3 + 2 \)
\( y = -1 \)
Ответ:\( (1; -1) \)
Условие: Решить графически систему уравнений \(3x + y = 2\) и \(x — 2y = 3\).
Решение:
Выразим \(y\)
из первого уравнения:
\(y = 2 — 3x\)
— линейная функция
Выразим \(y\)
из второго уравнения:
\(2y = x — 3\)
\(y = \frac{1}{2}x — \frac{3}{2}\)
— линейная функция
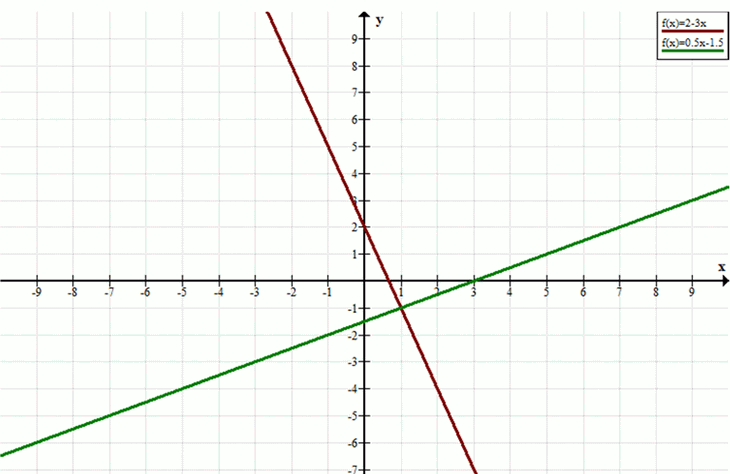
Построим графики обеих функций.
Найдем точку пересечения графиков.
Приравняем выражения для \(y\):
\(2 — 3x = \frac{1}{2}x — \frac{3}{2}\)
— приравнивание
Умножим обе части на 2:
\(4 — 6x = x — 3\)
— избавляемся от дроби
Перенесем члены с \(x\)
в одну сторону, а числа в другую:
\(4 + 3 = x + 6x\)
— группировка
\(7 = 7x\)
— сложение
Разделим на 7:
\(x = 1\)
— находим \(x\)
Подставим \(x = 1\)
в первое уравнение:
\(y = 2 — 3(1)\)
— подстановка
\(y = 2 — 3\)
— умножение
\(y = -1\)
— вычисление
Ответ: \( (1; -1) \)