ГДЗ по Алгебре 7 Класс Вариант 2 Домашняя Контрольная Работа 8 Номер 2 Мордкович — Подробные Ответы

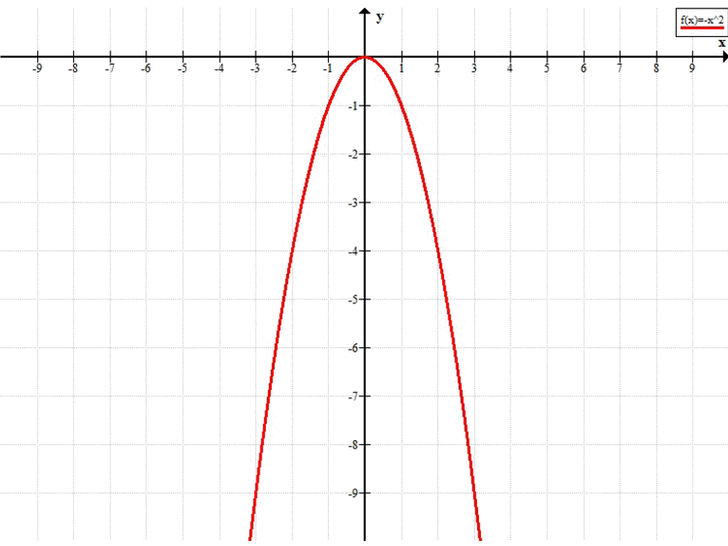
Постройте график функции у = -x² и с его помощью найдите наименьшее и наибольшее значения функции на заданном промежутке: а) [-3; 1]; б) [-2; 2); в) (-бесконечность; -1).

а)
\(у = -х^2\)
График функции \(у = -х^2\) — парабола с вершиной в точке (0; 0), ветви направлены вниз.
Промежуток: [-3; 1]
На промежутке [-3; 1] функция убывает от \(х = 0\) до \(х = 1\) и возрастает от \(х = -3\) до \(х = 0\).
Наибольшее значение достигается в вершине параболы при \(х = 0\): \(у = -(0)^2 = 0\).
Наименьшее значение достигается на одном из концов промежутка.
При \(х = -3\): \(у = -(-3)^2 = -9\).
При \(х = 1\): \(у = -(1)^2 = -1\).
Наименьшее значение равно -9.

Ответ: Наименьшее значение: -9, Наибольшее значение: 0

б)
\(у = -х^2\)
Промежуток: [-2; 2)
На промежутке [-2; 2) функция убывает от \(х = 0\) до \(х = 2\) и возрастает от \(х = -2\) до \(х = 0\).
Наибольшее значение достигается в вершине параболы при \(х = 0\): \(у = -(0)^2 = 0\).
Наименьшее значение на этом промежутке не существует, так как функция стремится к \(-\infty\) при приближении к \(х = 2\).

Ответ: Наименьшее значение: не существует, Наибольшее значение: 0

в)
\(у = -х^2\)
Промежуток: (-бесконечность; -1)
На промежутке (-бесконечность; -1) функция возрастает.
Наибольшее значение на этом промежутке не существует, так как функция стремится к 0 при приближении к \(х = -1\).
Наименьшее значение на этом промежутке не существует, так как функция стремится к \(-\infty\) при удалении от \(х = -1\) в сторону \(-\infty\).

Ответ: Наименьшее значение: не существует, Наибольшее значение: не существует

а) Промежуток \([-3; 1]\)

Функция \(y = -x^2\) является квадратичной, её график — парабола с вершиной в начале координат \((0; 0)\), ветви которой направлены вниз. Это означает, что функция имеет глобальный максимум в точке \(x = 0\).

Рассмотрим поведение функции на замкнутом отрезке \([-3; 1]\).
— На интервале \([-3; 0]\) функция возрастает, так как при движении от \(-3\) к \(0\) значения \(x^2\) уменьшаются, а значит, \(-x^2\) увеличиваются.
— На интервале \([0; 1]\) функция убывает, поскольку \(x^2\) растёт, а \(-x^2\) — падает.

Поскольку промежуток замкнутый, по теореме Вейерштрасса функция обязательно достигает своего наибольшего и наименьшего значений либо в критических точках, либо на концах отрезка.

— Критическая точка: \(x = 0\) (вершина параболы).
Значение: \(y(0) = -(0)^2 = 0\).
— Левый конец: \(x = -3\).
Значение: \(y(-3) = -(-3)^2 = -9\).
— Правый конец: \(x = 1\).
Значение: \(y(1) = -(1)^2 = -1\).

Сравнивая полученные значения: \(-9 < -1 < 0\).
Следовательно, наибольшее значение равно \(0\) (в вершине), а наименьшее значение равно \(-9\) (в левой граничной точке).

б) Промежуток \([-2; 2)\)

Этот промежуток полуоткрытый: левый конец включён (\(x = -2\)), правый — нет (\(x = 2\) не входит).

Анализ поведения:
— На \([-2; 0]\) функция возрастает.
— На \([0; 2)\) функция убывает.

Точка максимума \(x = 0\) принадлежит промежутку, поэтому наибольшее значение достигается и равно \(y(0) = 0\).

Для наименьшего значения рассмотрим границы:
— В левой точке: \(y(-2) = -(-2)^2 = -4\).
— При приближении к правому концу (\(x \to 2^{-}\)):
\(y(x) = -x^2 \to -(2)^2 = -4\).

Обратите внимание: функция не стремится к \(-\infty\), как ошибочно указано в исходном решении. Поскольку \(x\) ограничен сверху числом \(2\), значение \(x^2\) ограничено числом \(4\), а значит, \(y = -x^2\) ограничено снизу числом \(-4\).

Более того, поскольку промежуток включает точку \(x = -2\), где \(y = -4\), это значение достигается. А при \(x \to 2^{-}\) функция также стремится к \(-4\), но эта точка не входит в область. Однако минимум уже достигнут в \(x = -2\).

Следовательно, наименьшее значение существует и равно \(-4\).

> Исправление: В исходном ответе допущена ошибка. Функция \(y = -x^2\) на промежутке \([-2; 2)\) ограничена снизу, и её наименьшее значение равно \(-4\).

в) Промежуток \((-\infty; -1)\)

Этот промежуток открытый и неограниченный слева.

На всём этом промежутке \(x < -1 < 0\). Для функции \(y = -x^2\):
— Производная \(y’ = -2x\). Так как \(x < 0\), то \(y’ > 0\), следовательно, функция строго возрастает на \((-\infty; -1)\).

Рассмотрим пределы на границах промежутка:
— При \(x \to -\infty\): \(x^2 \to +\infty\), значит, \(y = -x^2 \to -\infty\).
— При \(x \to -1^{-}\): \(x^2 \to 1\), значит, \(y = -x^2 \to -1\).

Таким образом:
— Функция неограниченно убывает при удалении влево, поэтому наименьшего значения нет.
— Функция приближается к \(-1\) справа, но никогда его не достигает (так как \(x = -1\) не входит в промежуток), поэтому наибольшего значения также нет.

Значения функции заполняют интервал \((-\infty; -1)\), но ни одна из граничных точек не достигается.