ГДЗ по Алгебре 7 Класс Вариант 2 Домашняя Контрольная Работа 8 Номер 5 Мордкович — Подробные Ответы

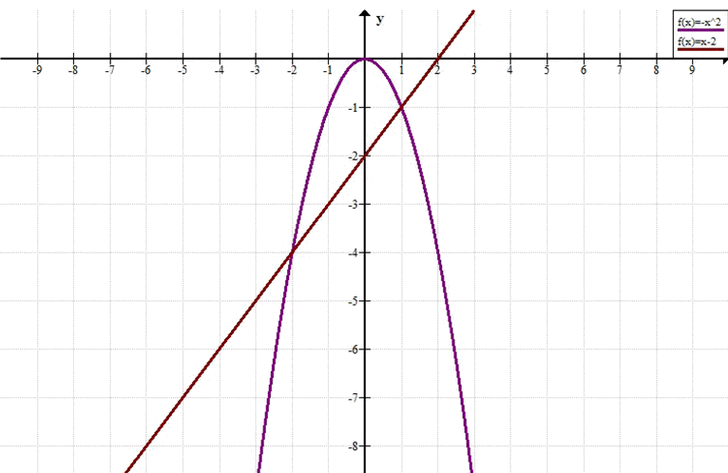
Решите графически уравнение -x² = х — 2.

5. Решите графически уравнение -х^2 = х — 2.
\( y = -x^2 \)
\( y = x — 2 \)
Построим графики функций.
Для \( y = -x^2 \): парабола с вершиной в (0,0), ветви направлены вниз.
Для \( y = x — 2 \): прямая, проходящая через точки (0, -2) и (2, 0).
Найдем точки пересечения графиков.
Приравняем выражения для y:
\( -x^2 = x — 2 \)
\( x^2 + x — 2 = 0 \)
Решим квадратное уравнение:
\( x = \frac{-1 \pm \sqrt{1^2 — 4(1)(-2)}}{2(1)} \)
\( x = \frac{-1 \pm \sqrt{1 + 8}}{2} \)
\( x = \frac{-1 \pm \sqrt{9}}{2} \)
\( x = \frac{-1 \pm 3}{2} \)
\( x_1 = \frac{-1 + 3}{2} = \frac{2}{2} = 1 \)
\( x_2 = \frac{-1 — 3}{2} = \frac{-4}{2} = -2 \)
Найдем соответствующие значения y:
Для \( x_1 = 1 \): \( y_1 = 1 — 2 = -1 \)
Для \( x_2 = -2 \): \( y_2 = -2 — 2 = -4 \)
Точки пересечения: (1, -1) и (-2, -4).

Ответ: x = 1, x = -2

Условие: Решить графически уравнение \( -x^2 = x — 2 \)

Решение:
Для решения уравнения графически, построим графики двух функций: \( y = -x^2 \) и \( y = x — 2 \). Точки пересечения этих графиков будут являться решениями уравнения.

График функции \( y = -x^2 \) — это парабола, ветви которой направлены вниз, с вершиной в точке (0, 0).

График функции \( y = x — 2 \) — это прямая линия с угловым коэффициентом 1 и сдвигом по оси y на -2.

Найдем точки пересечения, приравняв правые части уравнений:
\( -x^2 = x — 2 \)

Перенесем все члены в одну сторону, чтобы получить квадратное уравнение:
\( x^2 + x — 2 = 0 \)

Решим это квадратное уравнение, например, с помощью дискриминанта.
\( D = b^2 — 4ac \)
\( D = 1^2 — 4(1)(-2) \)
\( D = 1 + 8 \)
\( D = 9 \)

Найдем корни уравнения:
\( x_1 = \frac{-b + \sqrt{D}}{2a} \)
\( x_1 = \frac{-1 + \sqrt{9}}{2(1)} \)
\( x_1 = \frac{-1 + 3}{2} \)
\( x_1 = \frac{2}{2} \)
\( x_1 = 1 \)
\( x_2 = \frac{-b — \sqrt{D}}{2a} \)
\( x_2 = \frac{-1 — \sqrt{9}}{2(1)} \)
\( x_2 = \frac{-1 — 3}{2} \)
\( x_2 = \frac{-4}{2} \)
\( x_2 = -2 \)

Теперь найдем соответствующие значения y для каждой точки пересечения, подставив найденные x в любое из исходных уравнений. Возьмем \( y = x — 2 \).

Для \( x_1 = 1 \):
\( y_1 = 1 — 2 \)
\( y_1 = -1 \)
Точка пересечения: (1, -1)

Для \( x_2 = -2 \):
\( y_2 = -2 — 2 \)
\( y_2 = -4 \)
Точка пересечения: (-2, -4)

Таким образом, решениями уравнения являются значения x, равные 1 и -2.

Ответ: 1, -2