Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Вариант 2 Домашняя Контрольная Работа 8 Номер 6 Мордкович — Подробные Ответы
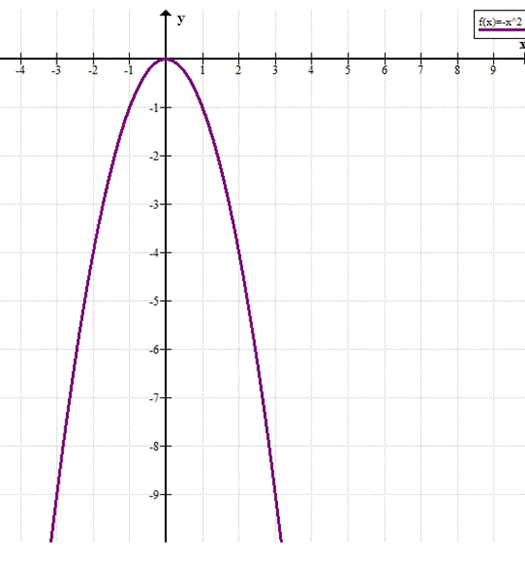
На графике функции у = -x² найдите точку, координаты которой — противоположные числа.
\( y = -x^2 \)
\( y = -x \)
\( -x^2 = -x \)
\( x^2 — x = 0 \)
\( x(x — 1) = 0 \)
\( x = 0 \) или \( x = 1 \)
Если \( x = 0 \), то \( y = -0^2 = 0 \). Точка (0, 0).
Если \( x = 1 \), то \( y = -1^2 = -1 \). Точка (1, -1).
Противоположные числа — это числа, отличающиеся только знаком. В данном случае, нам нужна точка, где \( y = -x \).
Подставим \( y = -x \) в уравнение функции:
\( -x = -x^2 \)
\( x^2 — x = 0 \)
\( x(x — 1) = 0 \)
\( x = 0 \) или \( x = 1 \)
Если \( x = 0 \), то \( y = -0 = 0 \). Точка (0, 0). Координаты не являются противоположными числами, кроме случая 0.
Если \( x = 1 \), то \( y = -1 \). Точка (1, -1). Координаты являются противоположными числами.
Условие: На графике функции \(у = -х^2\) найдите точку, координаты которой — противоположные числа.
Решение:
Пусть координаты искомой точки будут \((x, y)\).
По условию, координаты точки противоположны, то есть \(y = -x\).
Также точка лежит на графике функции \(у = -х^2\).
Подставим \(y = -x\) в уравнение функции:
\(-x = -x^2\)
Перенесем все члены в одну сторону:
\(x^2 — x = 0\)
Вынесем \(x\) за скобки:
\(x(x — 1) = 0\)
Это уравнение имеет два решения:
\(x = 0\) или \(x — 1 = 0\)
Если \(x = 0\), то \(y = -x = -0 = 0\). Получаем точку \((0, 0)\). Координаты 0 и 0 являются противоположными.
Если \(x — 1 = 0\), то \(x = 1\). Тогда \(y = -x = -1\). Получаем точку \((1, -1)\). Координаты 1 и -1 являются противоположными.
Ответ: \((0, 0)\) и \((1, -1)\)