ГДЗ по Алгебре 7 Класс Вариант 2 Домашняя Контрольная Работа 8 Номер 9 Мордкович — Подробные Ответы

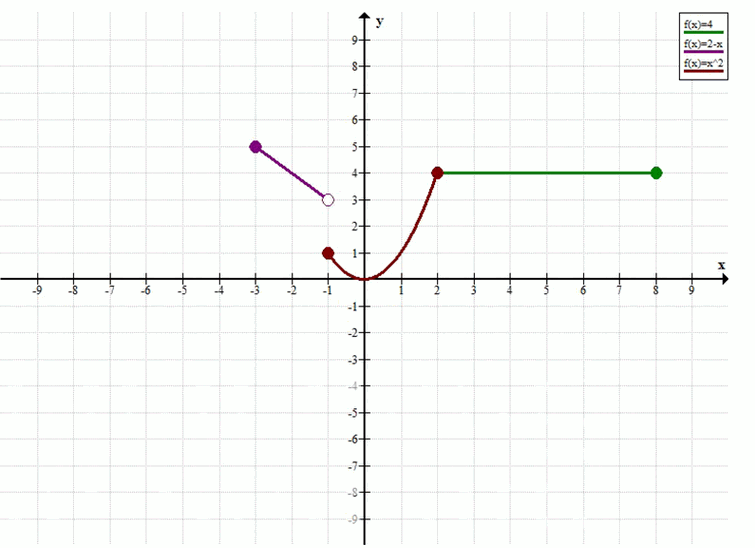
Постройте график функции у = f(x), где f(x) = система 2-х, если -3 ≤ х < -1; x², если -1 ≤ х ≤ 2; 4, если 2 < х ≤ 8. Используя построенный график функций, установите: а) какова область определения функции \(у = f(x)\); б) чему равны наименьшее и наибольшее значения функции; в) является ли функция непрерывной; г) при каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля; д) где функция возрастает, где убывает.

а) Область определения функции — это все допустимые значения аргумента \(x\).
Из определения функции видно, что она определена для \(x\) в интервалах \((-3, -1)\), \([-1, 2]\) и \((2, 8]\).
Объединяя эти интервалы, получаем область определения.
\( (-3, -1) \cup [-1, 2] \cup (2, 8] \)
\( (-3, 8] \)
Ответ: \( (-3, 8] \)

б) Наименьшее и наибольшее значения функции определяются по значениям \(y\) на графике.
На интервале \((-3, -1)\) функция постоянна и равна 2.
На интервале \([-1, 2]\) функция \(y = x^2\) возрастает от \( (-1)^2 = 1 \) до \( 2^2 = 4 \).
На интервале \((2, 8]\) функция постоянна и равна 4.
Наименьшее значение функции достигается на интервале \([-1, 2]\) при \(x = -1\), где \(y = (-1)^2 = 1\).
Наибольшее значение функции достигается на интервале \([-1, 2]\) при \(x = 2\) и на интервале \((2, 8]\), где \(y = 4\).
Ответ: Наименьшее значение: 1, Наибольшее значение: 4

в) Функция является непрерывной, если ее график можно нарисовать, не отрывая карандаша от бумаги.
Проверим точки «склейки»:
При \(x \to -1^-\), \(f(x) = 2\).
При \(x = -1\), \(f(-1) = (-1)^2 = 1\).
Так как \(2 \neq 1\), функция имеет разрыв в точке \(x = -1\).
При \(x \to 2^-\), \(f(x) = x^2 \to 2^2 = 4\).
При \(x \to 2^+\), \(f(x) = 4\).
В точке \(x = 2\) функция непрерывна.
Ответ: Нет

г) Значение функции равно нулю, больше нуля, меньше нуля.
На интервале \((-3, -1)\), \(f(x) = 2\). Значение функции всегда больше нуля.
На интервале \([-1, 2]\), \(f(x) = x^2\).
\(f(x) = 0\) при \(x = 0\).
\(f(x) > 0\) при \(x \in [-1, 0) \cup (0, 2]\).
На интервале \((2, 8]\), \(f(x) = 4\). Значение функции всегда больше нуля.
Значение функции равно нулю при \(x = 0\).
Значение функции больше нуля при \(x \in (-3, -1) \cup [-1, 0) \cup (0, 2] \cup (2, 8]\), что равно \(x \in (-3, 8]\) и \(x \neq 0\).
Значение функции меньше нуля нигде не достигается.
Ответ: Значение функции равно нулю при \(x = 0\). Значение функции больше нуля при \(x \in (-3, 8]\) и \(x \neq 0\). Значение функции меньше нуля нигде не достигается.

д) Где функция возрастает, где убывает.
На интервале \((-3, -1)\), функция постоянна.
На интервале \([-1, 0]\), функция \(y = x^2\) убывает.
На интервале \([0, 2]\), функция \(y = x^2\) возрастает.
На интервале \((2, 8]\), функция постоянна.
Ответ: Функция убывает на интервале \([-1, 0]\). Функция возрастает на интервале \([0, 2]\). Функция постоянна на интервалах \((-3, -1)\) и \((2, 8]\).

Условие: Построить график функции \(f(x)\) и проанализировать ее свойства.

Решение:
Функция задана кусочно:
\( f(x) = \begin{cases} 2, & \text{если } -3 \le x < -1 \\ x^2, & \text{если } -1 \le x \le 2 \\ 4, & \text{если } 2 < x \le 8 \end{cases} \)

Построение графика:
1. Для \( -3 \le x < -1 \), график — горизонтальная линия \( y = 2 \). Начальная точка \( (-3, 2) \) включена, конечная точка \( (-1, 2) \) не включена.
2. Для \( -1 \le x \le 2 \), график — часть параболы \( y = x^2 \). Точка \( (-1, (-1)^2) = (-1, 1) \) включена. Точка \( (2, 2^2) = (2, 4) \) включена.
3. Для \( 2 < x \le 8 \), график — горизонтальная линия \( y = 4 \). Начальная точка \( (2, 4) \) не включена, конечная точка \( (8, 4) \) включена.

Анализ свойств функции по графику:

а) Область определения функции \(у = f(x)\):
Область определения — это все допустимые значения аргумента \(x\). По условию, функция определена на интервалах \( [-3, -1) \), \( [-1, 2] \) и \( (2, 8] \). Объединяя эти интервалы, получаем:
\( D(f) = [-3, 8] \)

б) Наименьшее и наибольшее значения функции:
На интервале \( [-3, -1) \), \( y = 2 \).
На интервале \( [-1, 2] \), функция \( y = x^2 \) возрастает от \( (-1)^2 = 1 \) до \( 2^2 = 4 \). Наименьшее значение на этом участке равно 1 (при \( x = -1 \)), наибольшее равно 4 (при \( x = 2 \)).
На интервале \( (2, 8] \), \( y = 4 \).
Сравнивая значения на всех участках: наименьшее значение функции равно 1 (достигается при \( x = -1 \)), наибольшее значение функции равно 4 (достигается при \( x = 2 \) и на всем интервале \( (2, 8] \)).

в) Является ли функция непрерывной:
Функция непрерывна на каждом из интервалов, где она задана одной формулой. Проверим точки «склейки»:
При \( x = -1 \):
Левый предел: \( \lim_{x \to -1^-} f(x) = \lim_{x \to -1^-} 2 = 2 \)
Значение функции: \( f(-1) = (-1)^2 = 1 \)
Правый предел: \( \lim_{x \to -1^+} f(x) = \lim_{x \to -1^+} x^2 = (-1)^2 = 1 \)
Так как левый предел не равен значению функции и правому пределу, функция имеет разрыв в точке \( x = -1 \).

При \( x = 2 \):
Левый предел: \( \lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} x^2 = 2^2 = 4 \)
Значение функции: \( f(2) = 2^2 = 4 \)
Правый предел: \( \lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} 4 = 4 \)
В точке \( x = 2 \) функция непрерывна.
Следовательно, функция не является непрерывной на всей своей области определения.

г) При каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля:
Значение функции равно нулю:
На интервале \( [-3, -1) \), \( f(x) = 2 \ne 0 \).
На интервале \( [-1, 2] \), \( f(x) = x^2 \). \( x^2 = 0 \) при \( x = 0 \).
На интервале \( (2, 8] \), \( f(x) = 4 \ne 0 \).
Значение функции равно нулю при \( x = 0 \).

Значение функции больше нуля:
На интервале \( [-3, -1) \), \( f(x) = 2 > 0 \).
На интервале \( [-1, 2] \), \( f(x) = x^2 \). \( x^2 > 0 \) при \( x \ne 0 \). Так как \( x \in [-1, 2] \), то \( x^2 > 0 \) для \( x \in [-1, 0) \cup (0, 2] \).
На интервале \( (2, 8] \), \( f(x) = 4 > 0 \).
Значение функции больше нуля при \( x \in [-3, -1) \cup [-1, 0) \cup (0, 2] \cup (2, 8] \), что равно \( x \in [-3, 0) \cup (0, 8] \).

Значение функции меньше нуля:
На всех заданных интервалах значения функции неотрицательны.
Значение функции меньше нуля никогда не достигается.

д) Где функция возрастает, где убывает:
На интервале \( [-3, -1) \), функция постоянна \( y = 2 \).

На интервале \( [-1, 2] \), функция \( y = x^2 \). Эта часть параболы возрастает при \( x \ge 0 \).
Функция возрастает на \( [0, 2] \).
Функция убывает на \( [-1, 0] \).

На интервале \( (2, 8] \), функция постоянна \( y = 4 \).

Итого:
Функция возрастает на \( [0, 2] \).
Функция убывает на \( [-1, 0] \).
Функция постоянна на \( [-3, -1) \) и \( (2, 8] \).

Ответы:
а) Область определения: \( [-3, 8] \)
б) Наименьшее значение: 1, Наибольшее значение: 4
в) Функция не является непрерывной (разрыв в точке \( x = -1 \))
г) Значение функции равно нулю при \( x = 0 \). Значение функции больше нуля при \( x \in [-3, 0) \cup (0, 8] \). Значение функции меньше нуля никогда не достигается.
д) Функция возрастает на \( [0, 2] \). Функция убывает на \( [-1, 0] \).