Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 1.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте график заданной функции, найдите область определения и область значений функции:
а)
б)
Построить график заданной функции, найти область определения и область значений функции:
а)
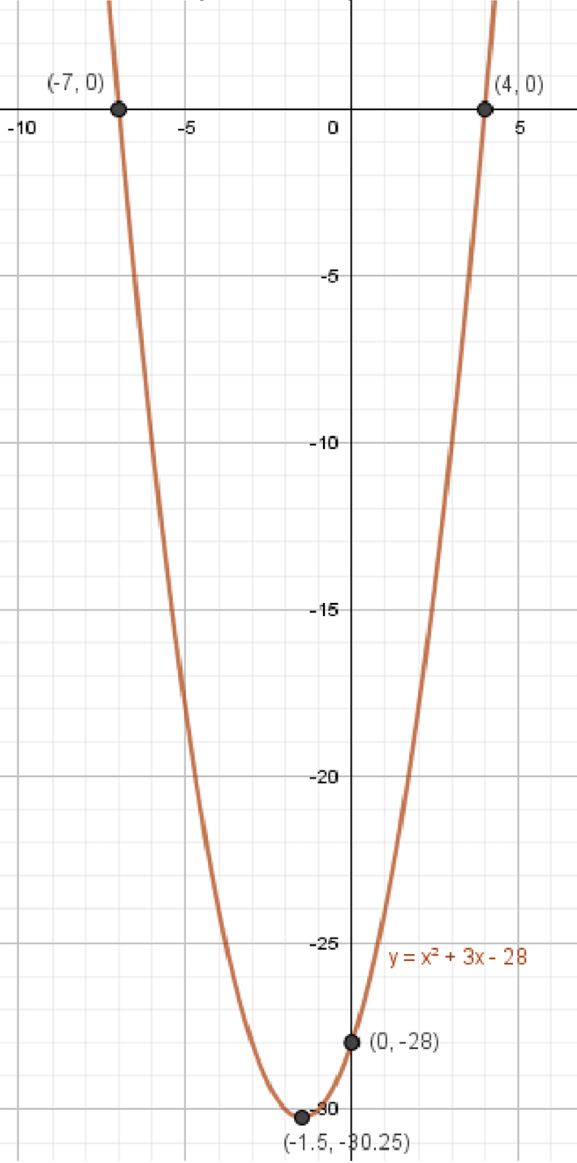
Координаты вершины параболы:
Координаты некоторых точек:
График функции:
Ответ:
б)
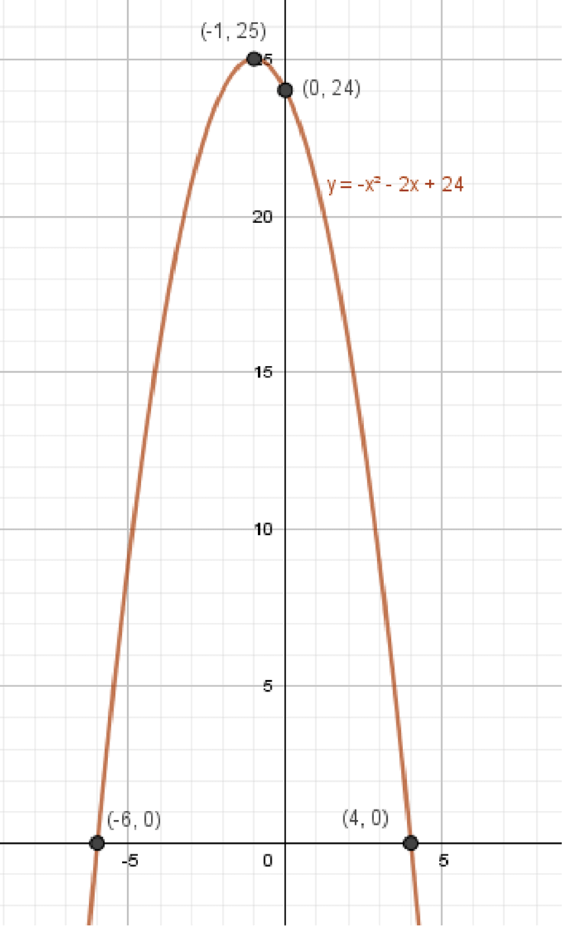
Координаты вершины параболы:
Координаты некоторых точек:
График функции:
Ответ:
а)
Шаг 1: Область определения
Функция является квадратичной, и все квадратичные функции определены для всех значений , так как нет ограничений на значение . Следовательно, область определения этой функции:
Шаг 2: Координаты вершины параболы
Для нахождения координат вершины параболы, нужно использовать формулу для , абсциссы вершины параболы:
где — коэффициент при , а — коэффициент при .
Подставляем значения:
Таким образом, абсцисса вершины параболы .
Теперь находим ординату вершины , подставив в уравнение функции:
Выполним вычисления:
Таким образом, координаты вершины параболы .
Шаг 3: Координаты некоторых точек
Для построения графика выберем несколько значений и вычислим соответствующие значения :
- При :
Точка .
- При :
Точка .
- При :
Точка .
Таким образом, у нас есть точки , , , которые можно использовать для построения графика.
Шаг 4: График функции
График функции будет представлять собой параболу, направленную вверх (так как коэффициент при положительный). Вершина будет в точке , и парабола будет открываться вверх.
График функции:
Шаг 5: Область значений
Парабола открывается вверх, поэтому её минимальное значение достигается в вершине. Минимальное значение в точке , и с увеличением значения возрастают. Следовательно, область значений функции:
Ответ:
б)
Шаг 1: Область определения
Функция является квадратичной, и для всех квадратичных функций область определения будет , так как нет ограничений на значение . Область определения:
Шаг 2: Координаты вершины параболы
Для нахождения координат вершины параболы используем формулу для :
где — коэффициент при , а — коэффициент при .
Подставляем значения:
Таким образом, абсцисса вершины .
Теперь находим ординату вершины , подставив в уравнение функции:
Выполним вычисления:
Таким образом, координаты вершины параболы .
Шаг 3: Координаты некоторых точек
Для построения графика выберем несколько значений и вычислим соответствующие значения :
- При :
Точка .
- При :
Точка .
- При :
Точка .
Таким образом, у нас есть точки , , , которые можно использовать для построения графика.
Шаг 4: График функции
График функции будет представлять собой параболу, направленную вниз (так как коэффициент при отрицательный). Вершина будет в точке , и парабола будет открываться вниз.
График функции:
Шаг 5: Область значений
Парабола открывается вниз, поэтому её максимальное значение достигается в вершине. Максимальное значение в точке , и с увеличением значения будут уменьшаться. Следовательно, область значений функции:
Ответ: