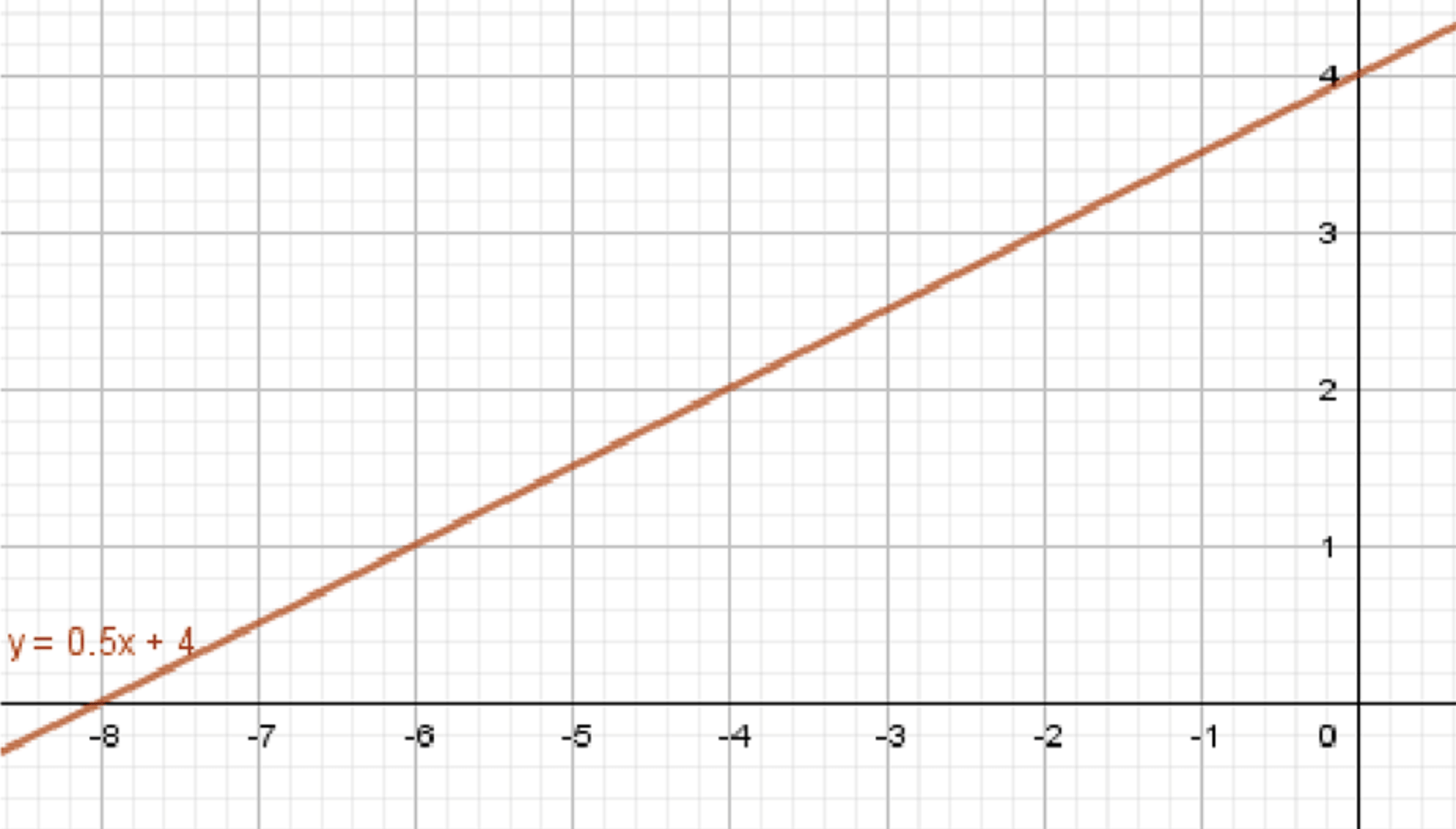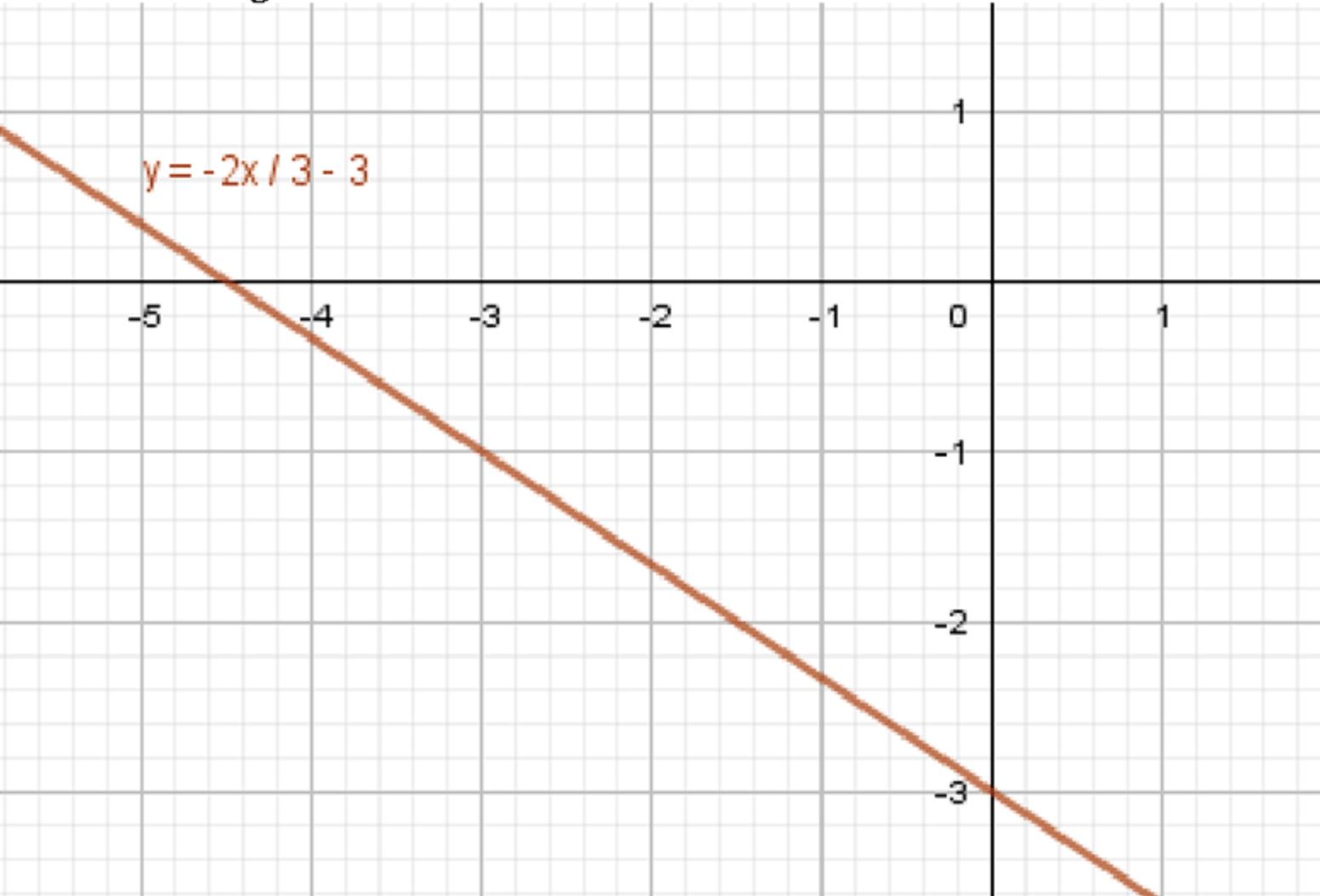Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 1.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте график заданной функции, найдите область определения и область значений функции:
а)
б)
в)
г)
Построить график заданной функции, найти область определения и область значений функции:
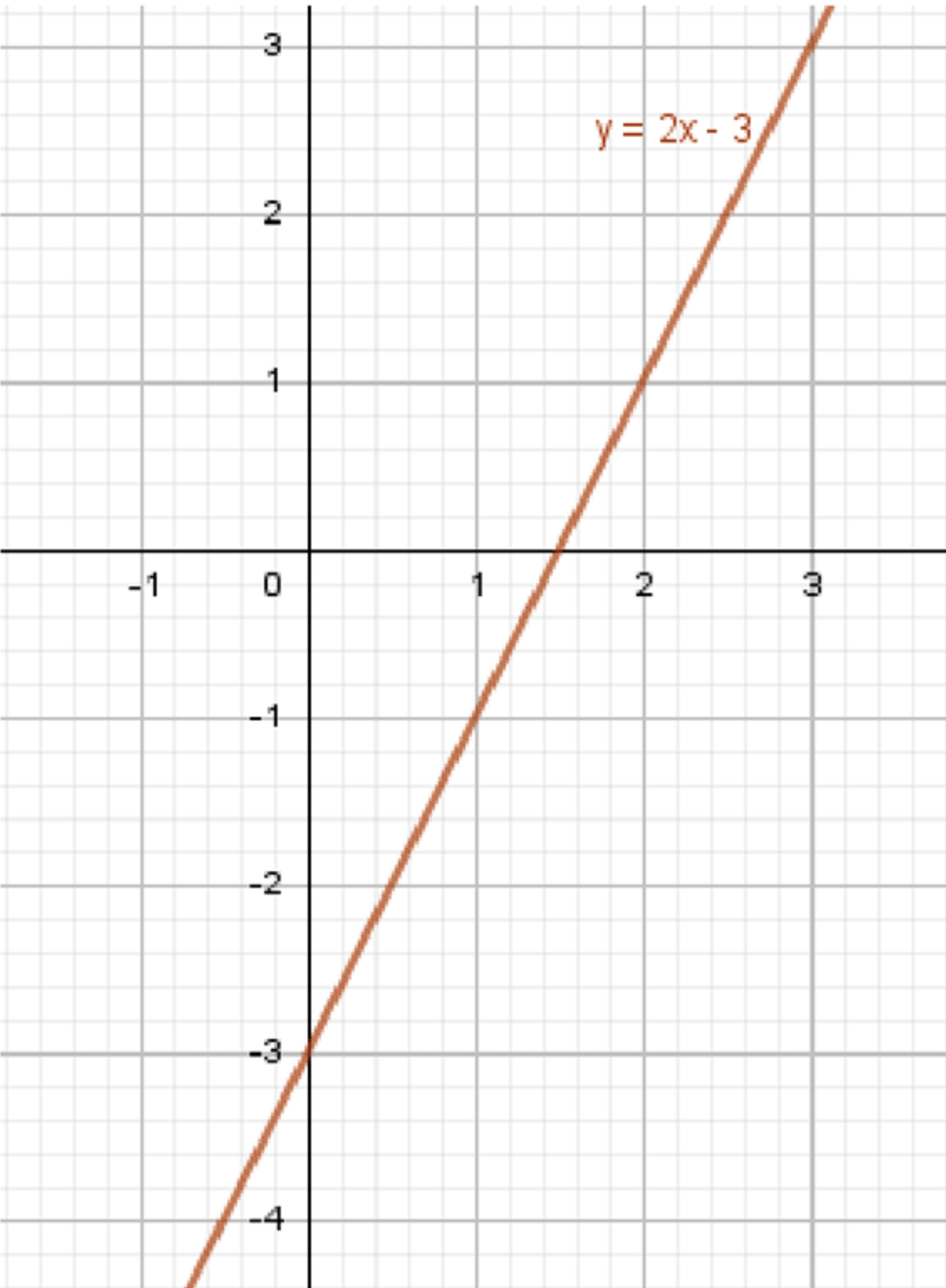
а)
Дано уравнение прямой:
График функции:
Ответ: .
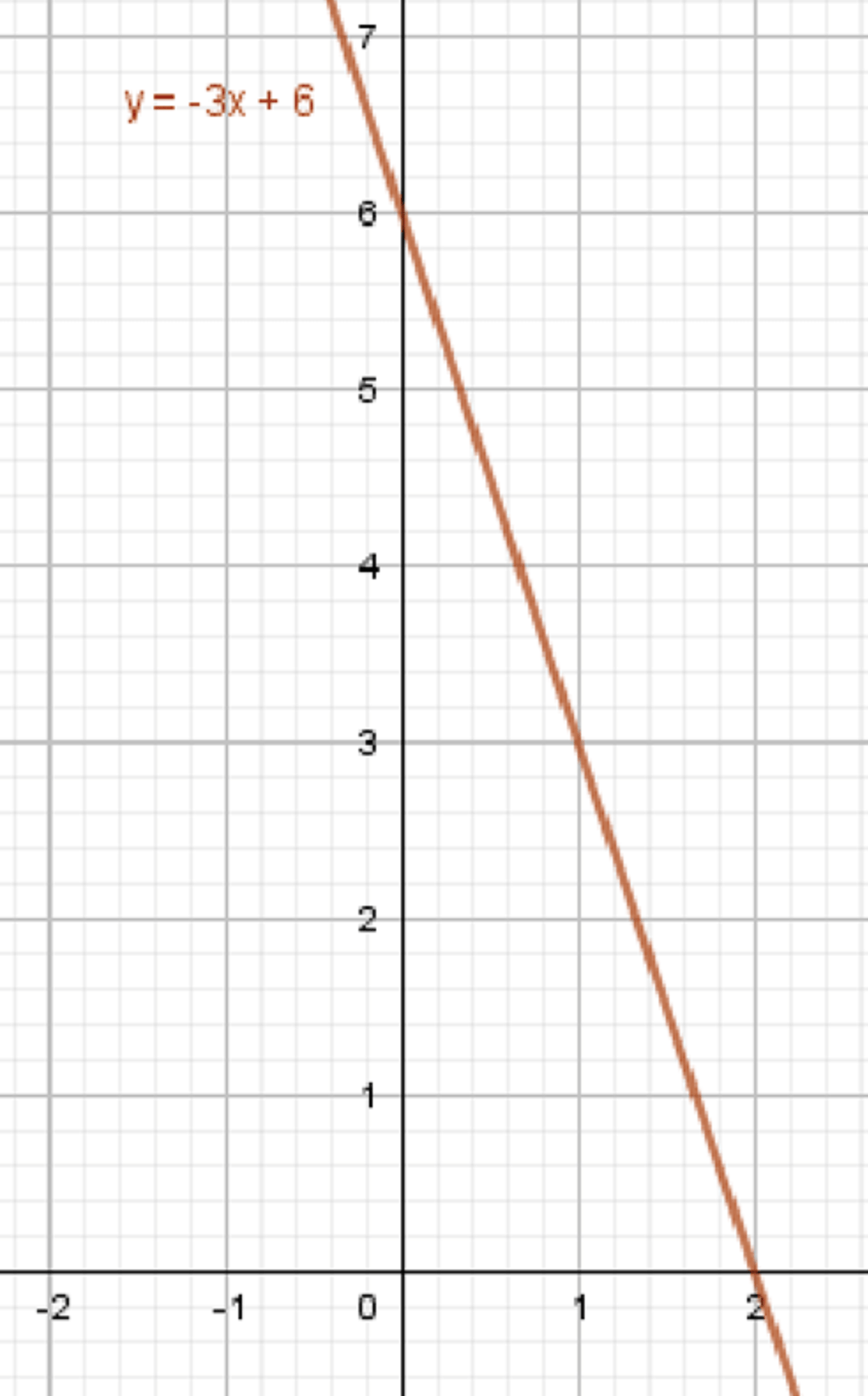
б)
Дано уравнение прямой:
График функции:
Ответ: .
в)
Дано уравнение прямой:
График функции:
Ответ: .
г)
Дано уравнение прямой:
График функции:
Ответ: .
а)
Шаг 1: Рассмотрим область определения (D).
Функция является линейной. Линейная функция определена для всех значений . Поэтому область определения функции:
Шаг 2: Рассмотрим область значений (E).
Линейная функция также может принимать любые значения , так как прямые линии могут пересекать любую вертикальную прямую (по оси ). Таким образом, область значений:
Шаг 3: Построение графика.
Для построения графика функции нужно найти несколько точек:
- При : . Точка .
- При : . Точка .
Эти две точки дают нам прямую, которая является графиком функции.
График функции:
Ответ: .
б)
Шаг 1: Рассмотрим область определения (D).
Функция также является линейной. Следовательно, она определена для всех значений . Таким образом, область определения:
Шаг 2: Рассмотрим область значений (E).
Как и предыдущая, эта функция также является линейной и может принимать любые значения . Поэтому область значений:
Шаг 3: Построение графика.
Для построения графика функции находим несколько точек:
- При : . Точка .
- При : . Точка .
Эти две точки тоже лежат на прямой, которая является графиком функции.
График функции:
Ответ: .
в)
Шаг 1: Рассмотрим область определения (D).
Функция является линейной, следовательно, она определена для всех значений . Область определения:
Шаг 2: Рассмотрим область значений (E).
Функция также линейная, а значит, она может принимать любые значения . Таким образом, область значений:
Шаг 3: Построение графика.
Для построения графика функции находим несколько точек:
- При : . Точка .
- При : . Точка .
Эти точки принадлежат прямой, которая и будет графиком функции.
График функции:
Ответ: .
г)
Шаг 1: Рассмотрим область определения (D).
Функция является линейной. Следовательно, она определена для всех значений . Область определения:
Шаг 2: Рассмотрим область значений (E).
Как и предыдущие функции, эта функция является линейной и может принимать любые значения . Таким образом, область значений:
Шаг 3: Построение графика.
Для построения графика функции находим несколько точек:
- При : . Точка .
- При : . Точка .
Эти точки принадлежат прямой, которая и будет графиком функции.
График функции:
Ответ: .