Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 10.22 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а)
б)
Решить графически уравнение:
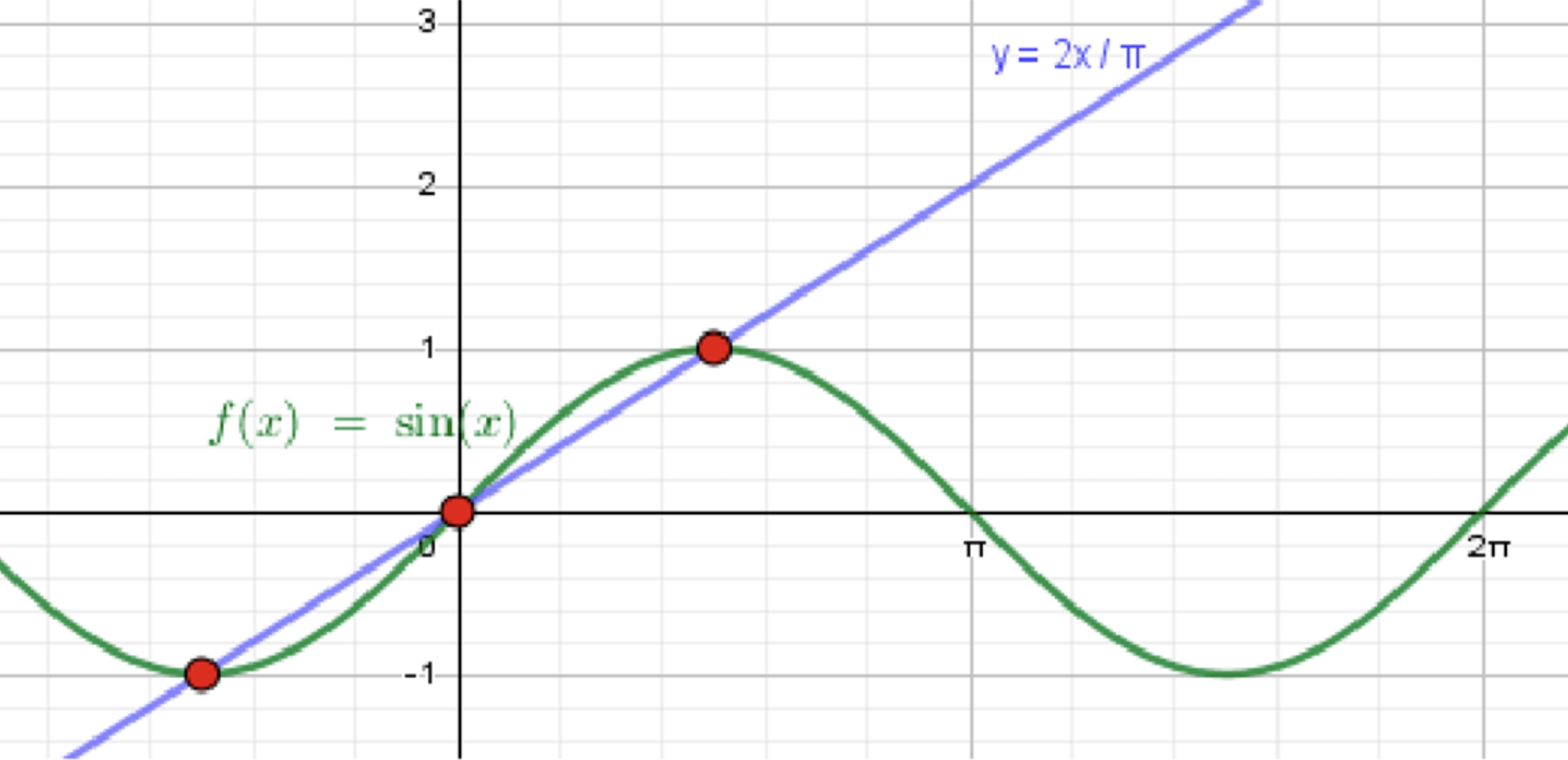
а)
— уравнение синусоиды;
— уравнение прямой;
| 0 | ||
|---|---|---|
| 0 | 2 |
Графики функций:
Ответ: ; .
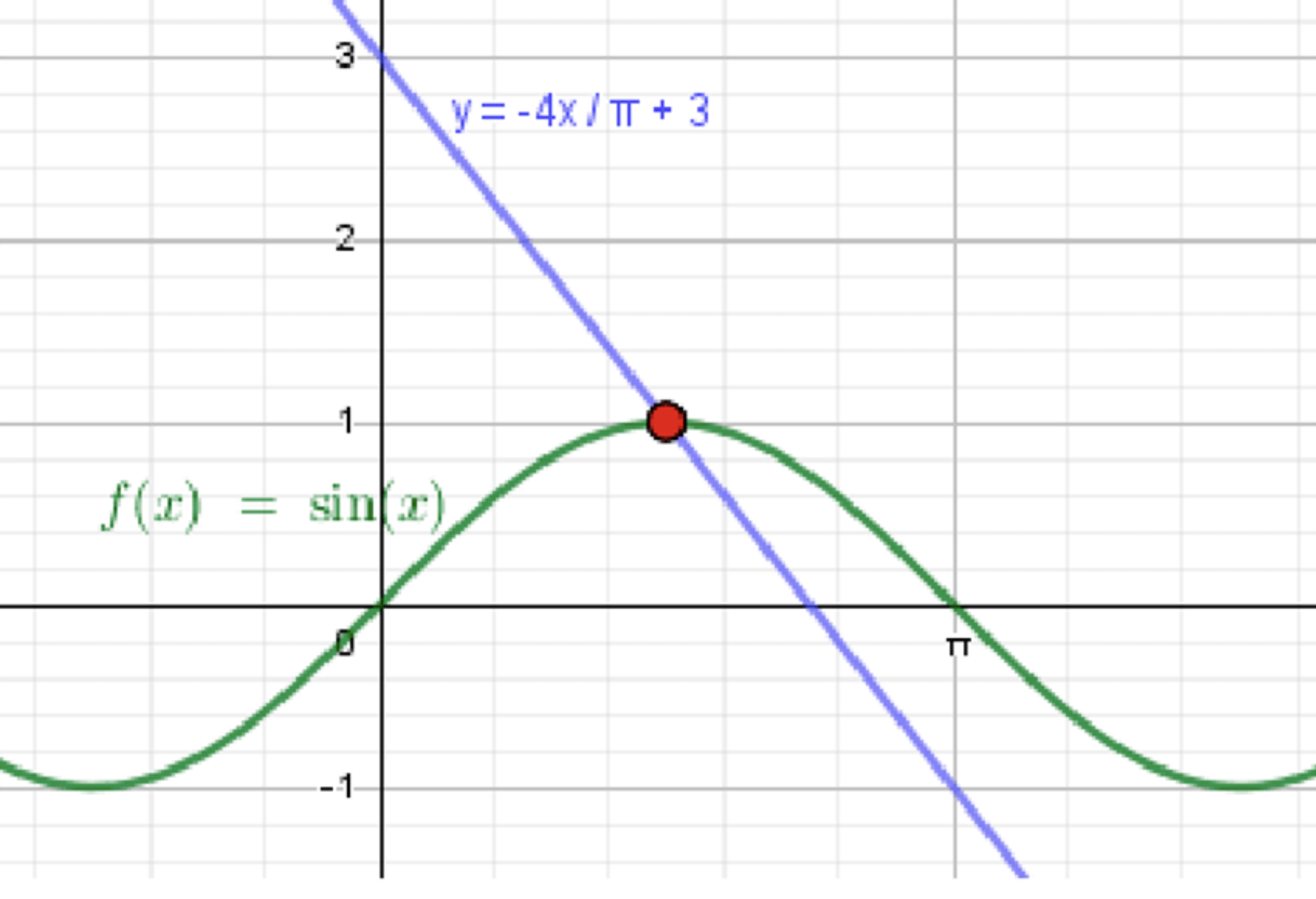
б)
— уравнение синусоиды;
— уравнение прямой;
| 0 | ||
|---|---|---|
| 3 | -1 |
Графики функций:
Ответ: .
а)
1) Что сравниваем
Слева — синусоида (чёткая периодическая, диапазон значений ).
Справа — прямая (проходит через начало координат, угловой коэффициент ).
2) Ограничим область возможных решений
Так как , то равенство возможно только там, где .
Отсюда .
Вне отрезка прямая даёт по модулю значения , а синус — нет, поэтому пересечений там быть не может.
3) Симметрия
— нечётная функция, и — тоже нечётная. Значит, если — решение, то и — решение. Достаточно найти решения на , а затем отзеркалить.
4) Проверим концы отрезка
- В точке : и — решение.
- В точке : и — ещё одно решение.
5) Почему других на нет
Рассмотрим .
- .
- на ⇒ вогнута вниз на всём отрезке.
У вогнутой функции, имеющей одинаковые значения на концах отрезка, внутри отрезка значения строго больше линейной интерполяции этих концов, то есть для .
Следовательно, внутри и равенство достигается только на концах.
С учётом нечётности получаем три и только три решения:
Ответ для (а): .
б)
1) Что сравниваем
Слева — та же синусоида .
Справа — прямая c отрицательным угловым коэффициентом и пересечением с осью в точке .
2) Ограничим область возможных решений по диапазону синуса
Чтобы мог равняться правой части, необходимо, чтобы правая часть лежала в :
Решим двойное неравенство по шагам:
Итак, возможные только из отрезка .
Вне его прямая даёт значения (при ) или (при ), и равенства с быть не может.
3) Проверим концы отрезка
- При : и — подходит.
- При : , а — не подходит.
4) Докажем единственность решения на
Введём .
Производная:
На имеем , поэтому
Следовательно, на всём отрезке строго возрастает. Так как , то:
- для получаем (равенство уже не выполняется),
- для мы вне допустимого отрезка (см. п.2).
Значит, на всей прямой существует ровно одно решение, и это .
Ответ для (б): .