Задача
Постройте и прочитайте график функции у = f(x):
а)
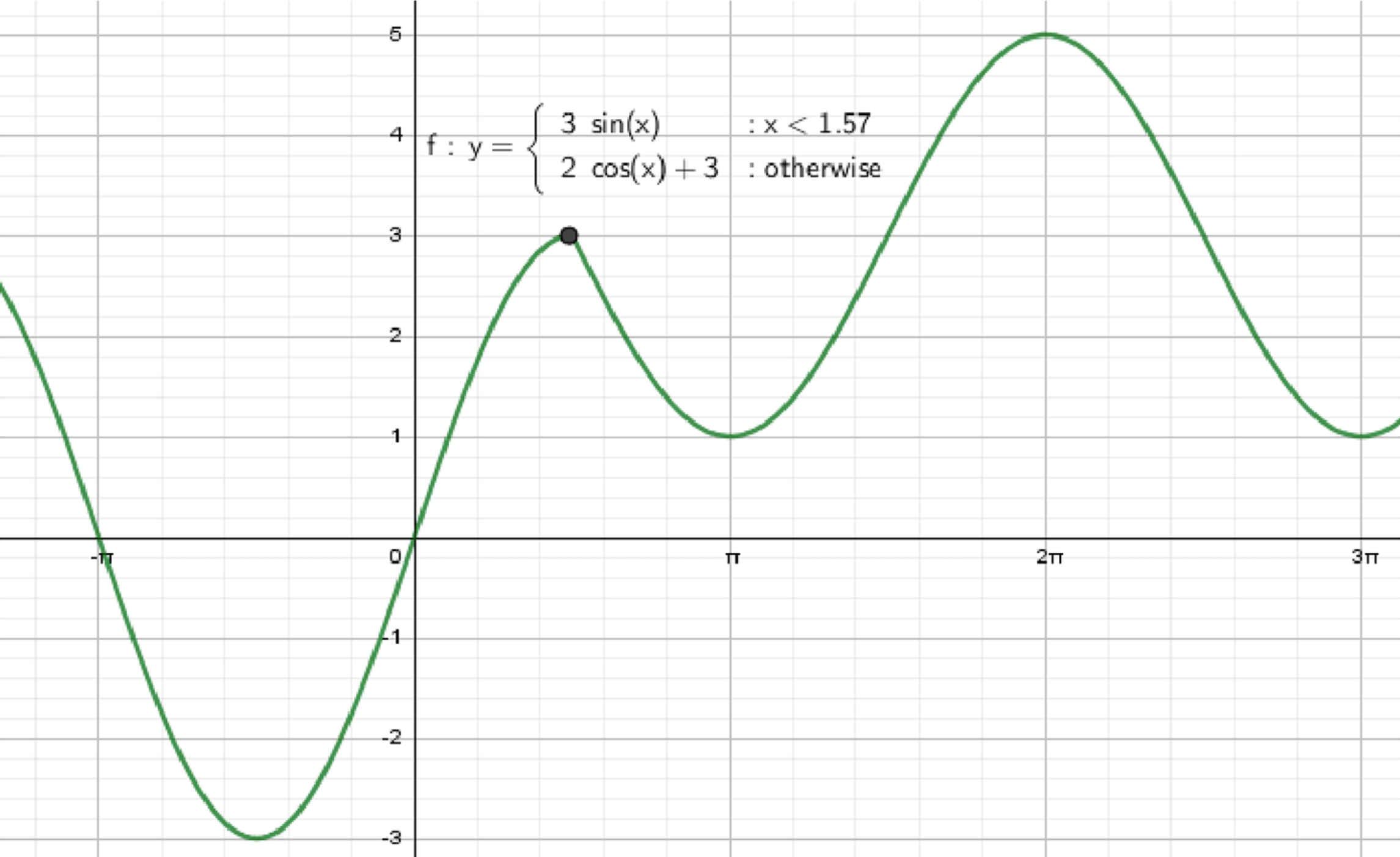
y = { 3 sin x , если x < π 2 2 cos x + 3 , если x ≥ π 2
б)
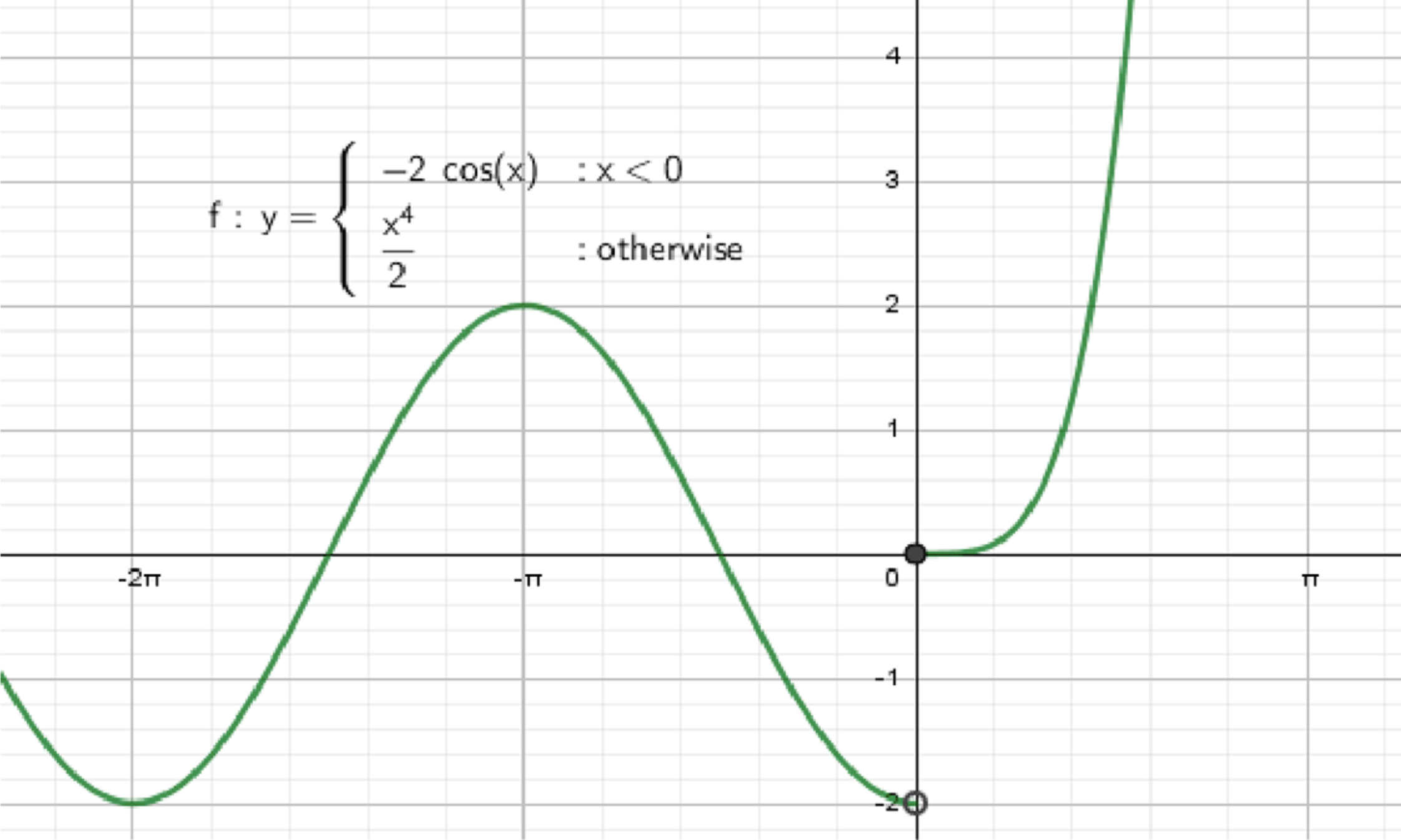
y = { − 2 cos x , если x < 0 1 2 x 4 , если x ≥ 0
Краткий ответ:
Построить и прочитать график функции y = f ( x ) y = f(x)
В данной задаче n n
а)
y = { 3 sin x , если x < π 2 2 cos x + 3 , если x ≥ π 2 y = \begin{cases} 3 \sin x, & \text{если } x < \frac{\pi}{2} \\ 2 \cos x + 3, & \text{если } x \geq \frac{\pi}{2} \end{cases}
y = 3 sin x y = 3 \sin x
y ( π 2 ) = 3 sin π 2 = 3 ⋅ 1 = 3 ; y\left(\frac{\pi}{2}\right) = 3 \sin \frac{\pi}{2} = 3 \cdot 1 = 3;
y = 2 cos x + 3 y = 2 \cos x + 3
y ( π 2 ) = 2 cos π 2 + 3 = 2 ⋅ 0 + 3 = 3 ; y\left(\frac{\pi}{2}\right) = 2 \cos \frac{\pi}{2} + 3 = 2 \cdot 0 + 3 = 3;
График функции:
Свойства функции:
D ( f ) = ( − ∞ ; + ∞ ) ; E ( f ) = [ − 3 ; 5 ] ; D(f) = (-\infty; +\infty); \quad E(f) = [-3; 5]; Возрастает на [ − π 2 − 2 π n ; π 2 − 2 π n ] ∪ [ π + 2 π n ; 2 π + 2 π n ] ; \left[-\frac{\pi}{2} — 2\pi n; \frac{\pi}{2} — 2\pi n\right] \cup [\pi + 2\pi n; 2\pi + 2\pi n]; Убывает на [ − 3 π 2 − 2 π n ; − π 2 − 2 π n ] ∪ [ π 2 ; π ] ∪ [ 2 π + 2 π n ; 3 π + 2 π n ] ; \left[-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right] \cup \left[\frac{\pi}{2}; \pi\right] \cup [2\pi + 2\pi n; 3\pi + 2\pi n]; f ( x ) > 0 f(x) > 0 ( − 2 π − 2 π n ; − π − 2 π n ) ∪ ( 0 ; + ∞ ) ; (-2\pi — 2\pi n; -\pi — 2\pi n) \cup (0; +\infty); f ( x ) < 0 f(x) < 0 ( − π − 2 π n ; − 2 π n ) ; (-\pi — 2\pi n; -2\pi n); Ограничена снизу и сверху; y min = y ( − π 2 ) = − 3 ; y_{\min} = y\left(-\frac{\pi}{2}\right) = -3; y max = y ( 2 π ) = 5 ; y_{\max} = y(2\pi) = 5; Ни четная, ни нечетная; Не является периодической; Непрерывна на ( − ∞ ; + ∞ ) ; (-\infty; +\infty); б)
y = { − 2 cos x , если x < 0 1 2 x 4 , если x ≥ 0 y = \begin{cases} -2 \cos x, & \text{если } x < 0 \\ \frac{1}{2} x^4, & \text{если } x \geq 0 \end{cases}
y = − 2 cos x y = -2 \cos x
y ( 0 ) = − 2 cos 0 = − 2 ⋅ 1 = − 2 ; y(0) = -2 \cos 0 = -2 \cdot 1 = -2;
y = 1 2 x 4 y = \frac{1}{2} x^4
x 0 = 0 , y 0 = 0 ; x_0 = 0, \quad y_0 = 0;
Таблица значений:
x 0 1 1.5 y 0 0.5 ≈ 2.5 \begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 1.5 \\ \hline y & 0 & 0.5 & \approx 2.5 \\ \hline \end{array}
Графики функции:
Свойства функции:
D ( f ) = ( − ∞ ; + ∞ ) ; E ( f ) = [ − 2 ; + ∞ ) ; D(f) = (-\infty; +\infty); \quad E(f) = [-2; +\infty); Возрастает на [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; + ∞ ) ; [-2\pi — 2\pi n; -\pi — 2\pi n] \cup [0; +\infty); Убывает на [ − π − 2 π n ; − 2 π n ] ; [-\pi — 2\pi n; -2\pi n]; f ( x ) > 0 f(x) > 0 ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( 0 ; + ∞ ) ; \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup (0; +\infty); f ( x ) < 0 f(x) < 0 ( − 5 π 2 − 2 π n ; − 3 π 2 − 2 π n ) ∪ ( − π 2 ; 0 ) ; \left(-\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n\right) \cup \left(-\frac{\pi}{2}; 0\right); Ограничена снизу; y min = y ( − 2 π ) = − 2 ; y_{\min} = y(-2\pi) = -2; Ни четная, ни нечетная; Не является периодической; Непрерывна на ( − ∞ ; 0 ) ∪ ( 0 ; + ∞ ) (-\infty; 0) \cup (0; +\infty) Подробный ответ:
Построить и прочитать график функции y = f ( x ) y = f(x)
В данной задаче n n
а)
y = { 3 sin x , если x < π 2 2 cos x + 3 , если x ≥ π 2 y = \begin{cases} 3 \sin x, & \text{если } x < \frac{\pi}{2} \\ 2 \cos x + 3, & \text{если } x \geq \frac{\pi}{2} \end{cases}
Разбор функции:
Первая часть функции: y = 3 sin x y = 3 \sin x x < π 2 x < \frac{\pi}{2}
y = 3 sin x y = 3 \sin x Максимальное значение синуса sin x \sin x y = 3 sin x y = 3 \sin x Минимальное значение sin x \sin x y = 3 sin x y = 3 \sin x Период функции sin x \sin x 2 π 2\pi x < π 2 x < \frac{\pi}{2} Для x < π 2 x < \frac{\pi}{2}
y ( π 2 ) = 3 sin π 2 = 3 ⋅ 1 = 3 y\left(\frac{\pi}{2}\right) = 3 \sin \frac{\pi}{2} = 3 \cdot 1 = 3
Это означает, что график синусоиды будет плавно возрастать от 0 до 3 на интервале x ∈ [ 0 ; π 2 ) x \in \left[0; \frac{\pi}{2}\right)
Вторая часть функции: y = 2 cos x + 3 y = 2 \cos x + 3 x ≥ π 2 x \geq \frac{\pi}{2}
y = 2 cos x + 3 y = 2 \cos x + 3 Период косинуса cos x \cos x 2 π 2\pi x ≥ π 2 x \geq \frac{\pi}{2} Для x = π 2 x = \frac{\pi}{2}
y ( π 2 ) = 2 cos π 2 + 3 = 2 ⋅ 0 + 3 = 3 y\left(\frac{\pi}{2}\right) = 2 \cos \frac{\pi}{2} + 3 = 2 \cdot 0 + 3 = 3
Таким образом, на интервале [ π 2 ; + ∞ ) \left[\frac{\pi}{2}; +\infty\right) y = 3 y = 3
График функции:
График состоит из двух частей:
Для x < π 2 x < \frac{\pi}{2} Для x ≥ π 2 x \geq \frac{\pi}{2} Свойства функции:
Область определения: D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) Область значений: E ( f ) = [ − 3 ; 5 ] E(f) = [-3; 5] Монотонность: Функция возрастает на интервалах: [ − π 2 − 2 π n ; π 2 − 2 π n ] ∪ [ π + 2 π n ; 2 π + 2 π n ] \left[-\frac{\pi}{2} — 2\pi n; \frac{\pi}{2} — 2\pi n\right] \cup [\pi + 2\pi n; 2\pi + 2\pi n] Функция убывает на интервалах: [ − 3 π 2 − 2 π n ; − π 2 − 2 π n ] ∪ [ π 2 ; π ] ∪ [ 2 π + 2 π n ; 3 π + 2 π n ] \left[-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right] \cup \left[\frac{\pi}{2}; \pi\right] \cup [2\pi + 2\pi n; 3\pi + 2\pi n] Значения функции: f ( x ) > 0 f(x) > 0 ( − 2 π − 2 π n ; − π − 2 π n ) ∪ ( 0 ; + ∞ ) (-2\pi — 2\pi n; -\pi — 2\pi n) \cup (0; +\infty) f ( x ) < 0 f(x) < 0 ( − π − 2 π n ; − 2 π n ) (-\pi — 2\pi n; -2\pi n) Ограниченность: Функция ограничена сверху и снизу:Минимальное значение y min = y ( − π 2 ) = − 3 y_{\min} = y\left(-\frac{\pi}{2}\right) = -3 Максимальное значение y max = y ( 2 π ) = 5 y_{\max} = y(2\pi) = 5 Симметрия: Функция не является ни четной, ни нечетной.Периодичность: Функция не является периодической, так как части функции не связаны между собой простыми периодами.Непрерывность: Функция непрерывна на всем ( − ∞ ; + ∞ ) (-\infty; +\infty) б)
y = { − 2 cos x , если x < 0 1 2 x 4 , если x ≥ 0 y = \begin{cases} -2 \cos x, & \text{если } x < 0 \\ \frac{1}{2} x^4, & \text{если } x \geq 0 \end{cases}
Разбор функции:
Первая часть функции: y = − 2 cos x y = -2 \cos x x < 0 x < 0
y = − 2 cos x y = -2 \cos x x x y y Период косинуса cos x \cos x 2 π 2\pi x < 0 x < 0 Для x = 0 x = 0
y ( 0 ) = − 2 cos 0 = − 2 ⋅ 1 = − 2 y(0) = -2 \cos 0 = -2 \cdot 1 = -2
Таким образом, на интервале ( − ∞ ; 0 ) (-\infty; 0) x x
Вторая часть функции: y = 1 2 x 4 y = \frac{1}{2} x^4 x ≥ 0 x \geq 0
Это параболическая функция с коэффициентом 1 2 \frac{1}{2} ( 0 , 0 ) (0, 0) Парабола не имеет ограничения сверху, она растет очень быстро с увеличением x x Для x = 1 x = 1
y ( 1 ) = 1 2 ⋅ 1 4 = 0.5 y(1) = \frac{1}{2} \cdot 1^4 = 0.5
Для x = 1.5 x = 1.5
y ( 1.5 ) = 1 2 ⋅ ( 1.5 ) 4 ≈ 2.5 y(1.5) = \frac{1}{2} \cdot (1.5)^4 \approx 2.5
Таблица значений:
x 0 1 1.5 y 0 0.5 ≈ 2.5 \begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 1.5 \\ \hline y & 0 & 0.5 & \approx 2.5 \\ \hline \end{array}
Графики функции:
График состоит из двух частей:
Для x < 0 x < 0 y y Для x ≥ 0 x \geq 0 ( 0 , 0 ) (0, 0) Свойства функции:
Область определения: D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) Область значений: E ( f ) = [ − 2 ; + ∞ ) E(f) = [-2; +\infty) Монотонность: Функция возрастает на интервалах: [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; + ∞ ) [-2\pi — 2\pi n; -\pi — 2\pi n] \cup [0; +\infty) Функция убывает на интервалах: [ − π − 2 π n ; − 2 π n ] [-\pi — 2\pi n; -2\pi n] Значения функции: f ( x ) > 0 f(x) > 0 ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( 0 ; + ∞ ) \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup (0; +\infty) f ( x ) < 0 f(x) < 0 ( − 5 π 2 − 2 π n ; − 3 π 2 − 2 π n ) ∪ ( − π 2 ; 0 ) \left(-\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n\right) \cup \left(-\frac{\pi}{2}; 0\right) Ограниченность: Функция ограничена снизу, минимальное значение y min = − 2 y_{\min} = -2 x = − 2 π x = -2\pi Симметрия: Функция не является ни четной, ни нечетной.Периодичность: Функция не является периодической.Непрерывность: Функция непрерывна на ( − ∞ ; 0 ) ∪ ( 0 ; + ∞ ) (-\infty; 0) \cup (0; +\infty)