Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 26.6 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте эскиз графика какой-нибудь функции y = f(x), обладающей заданными свойствами:
а)
б)
в)
г)
Построить эскиз графика какой-нибудь функции , обладающей указанными свойствами:
а)
б)
в)
г)
Когда даны односторонние пределы при , мы понимаем:
- Функция приближается к горизонтальной асимптоте;
- Поведение может быть различным вблизи (нет ограничений), но на бесконечности она должна стремиться к указанному числу;
- Мы можем использовать стандартные модификации экспоненциальных и дробно-рациональных функций для создания нужного поведения.
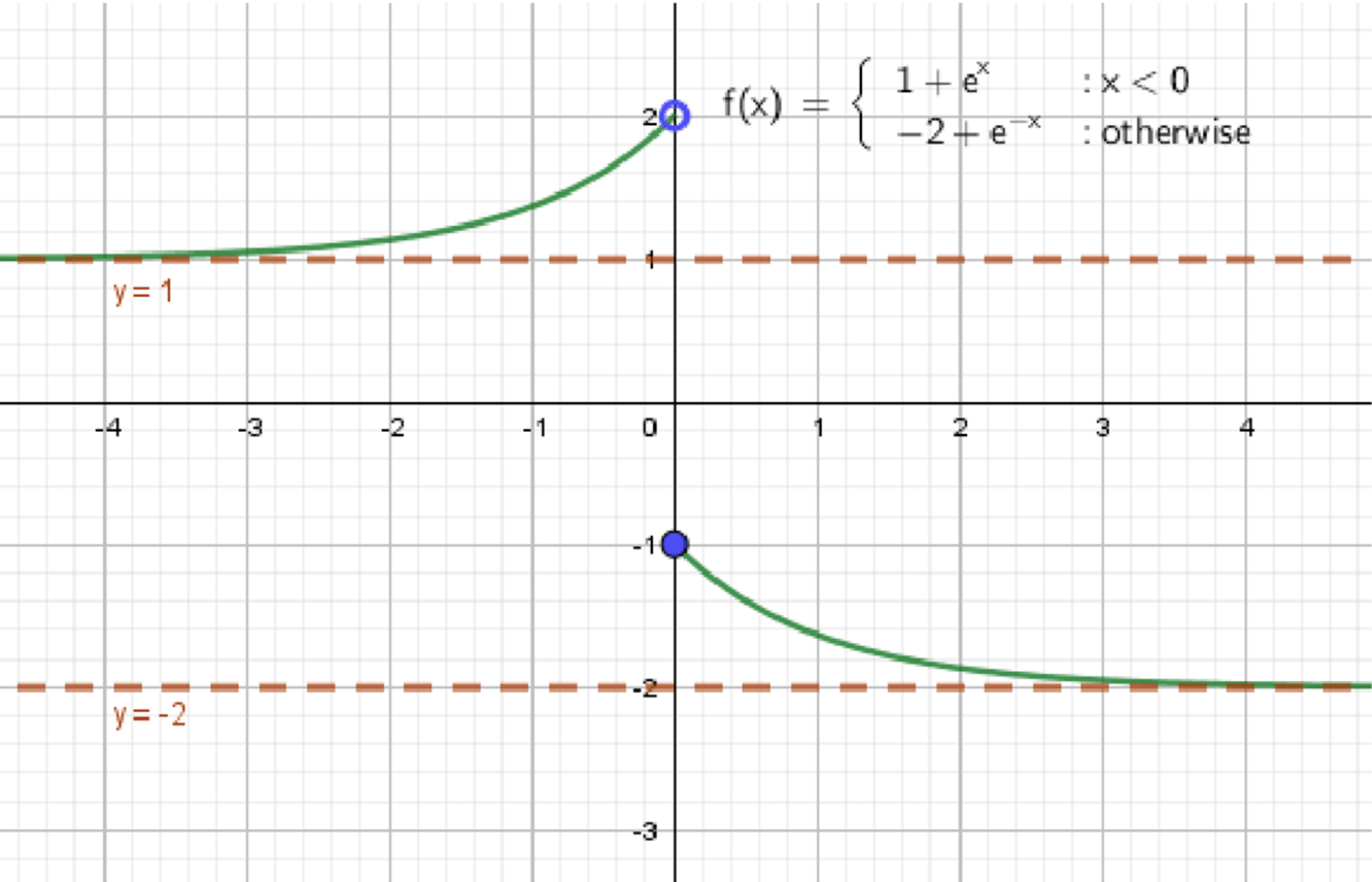
а) ,
Построение:
- Подходящий пример:
Проверка свойств:
- ;
- .
Как выглядит график:
- Гладкая кривая, возрастающая;
- При функция прижимается к оси ;
- При приближается к горизонтали ;
- Находится между этими значениями.
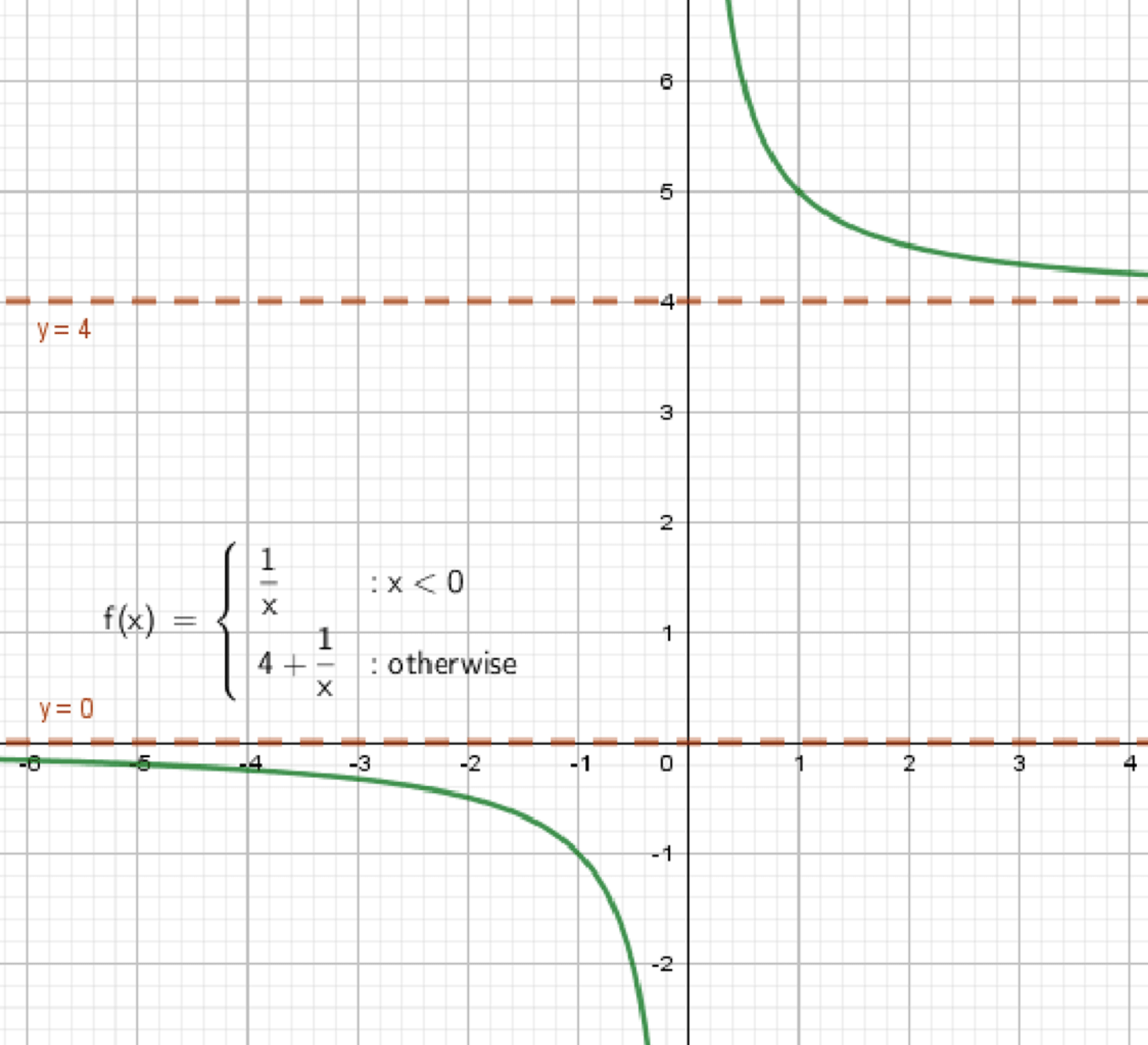
б) ,
Построение:
- Подходящий пример:
Проверка:
- ;
- .
Как выглядит график:
- Возрастающая функция;
- Горизонтальные асимптоты:
- слева;
- справа.
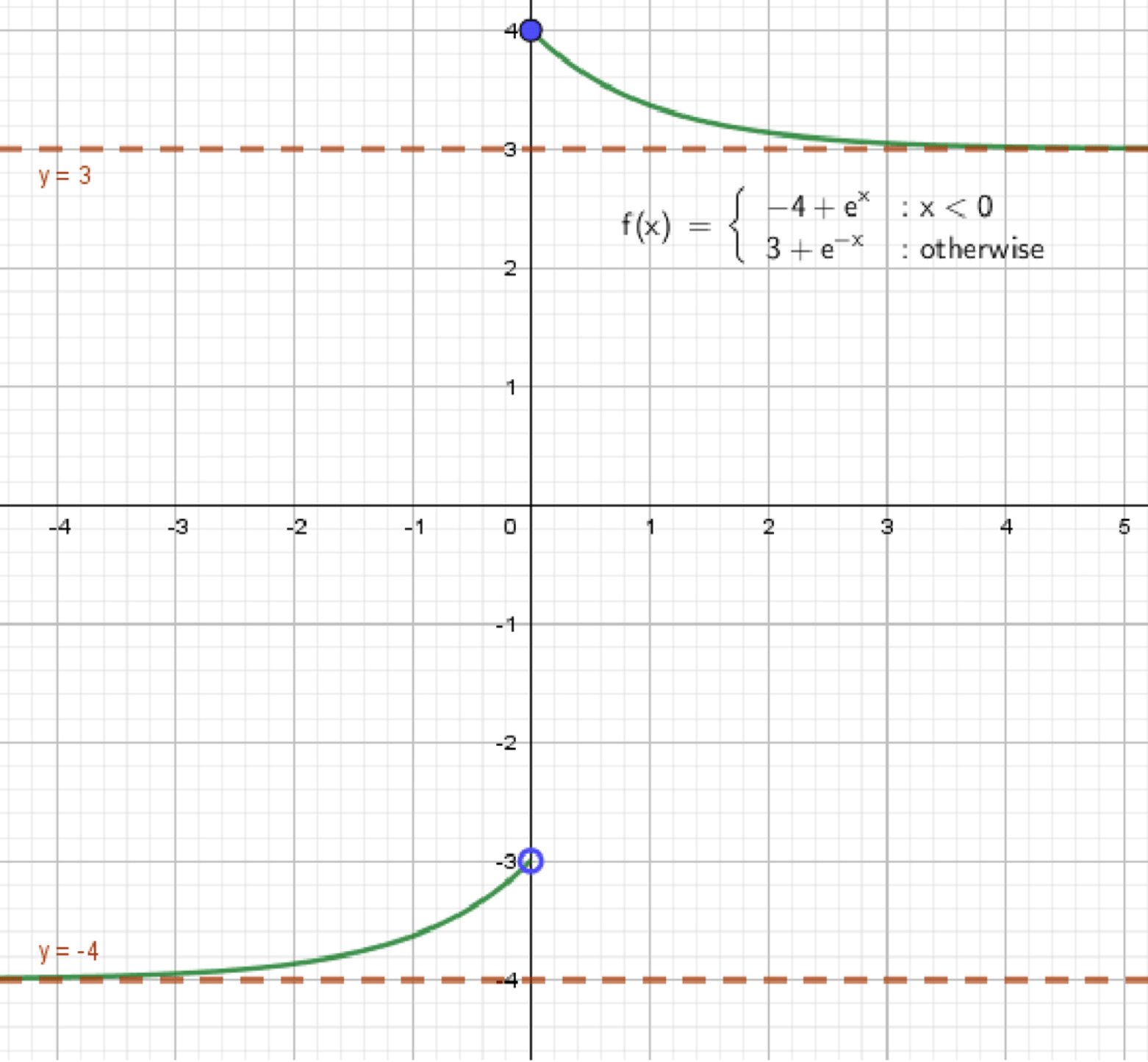
в) ,
Построение:
- Подходящий пример:
Проверка:
- ;
- .
Как выглядит график:
- Убывающая функция;
- Слева стремится к ;
- Справа стремится к .
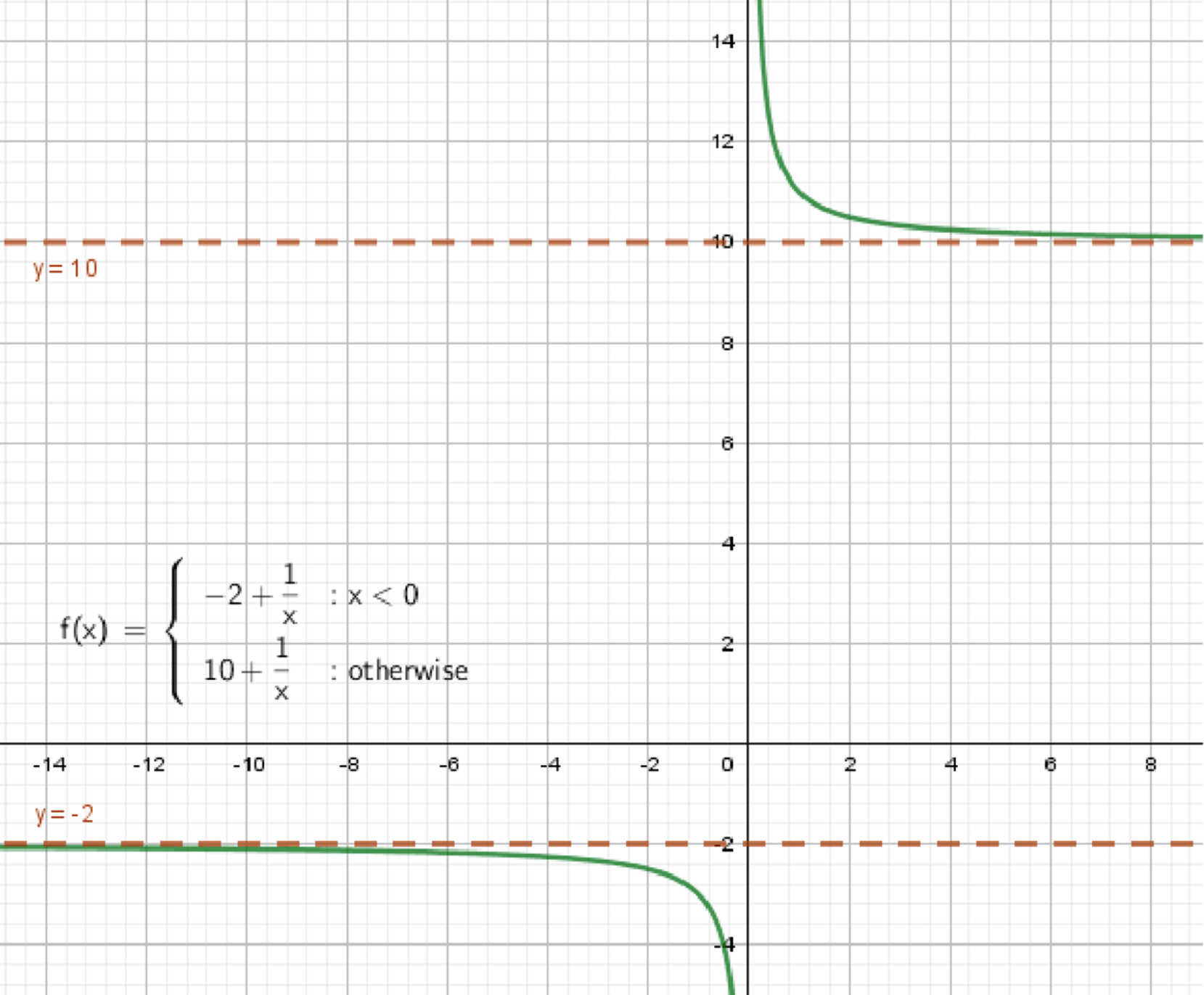
г) ,
Построение:
- Подходящий пример:
Проверка:
- ;
- .
Как выглядит график:
- Возрастающая кривая;
- Горизонтальные асимптоты:
- слева;
- справа.