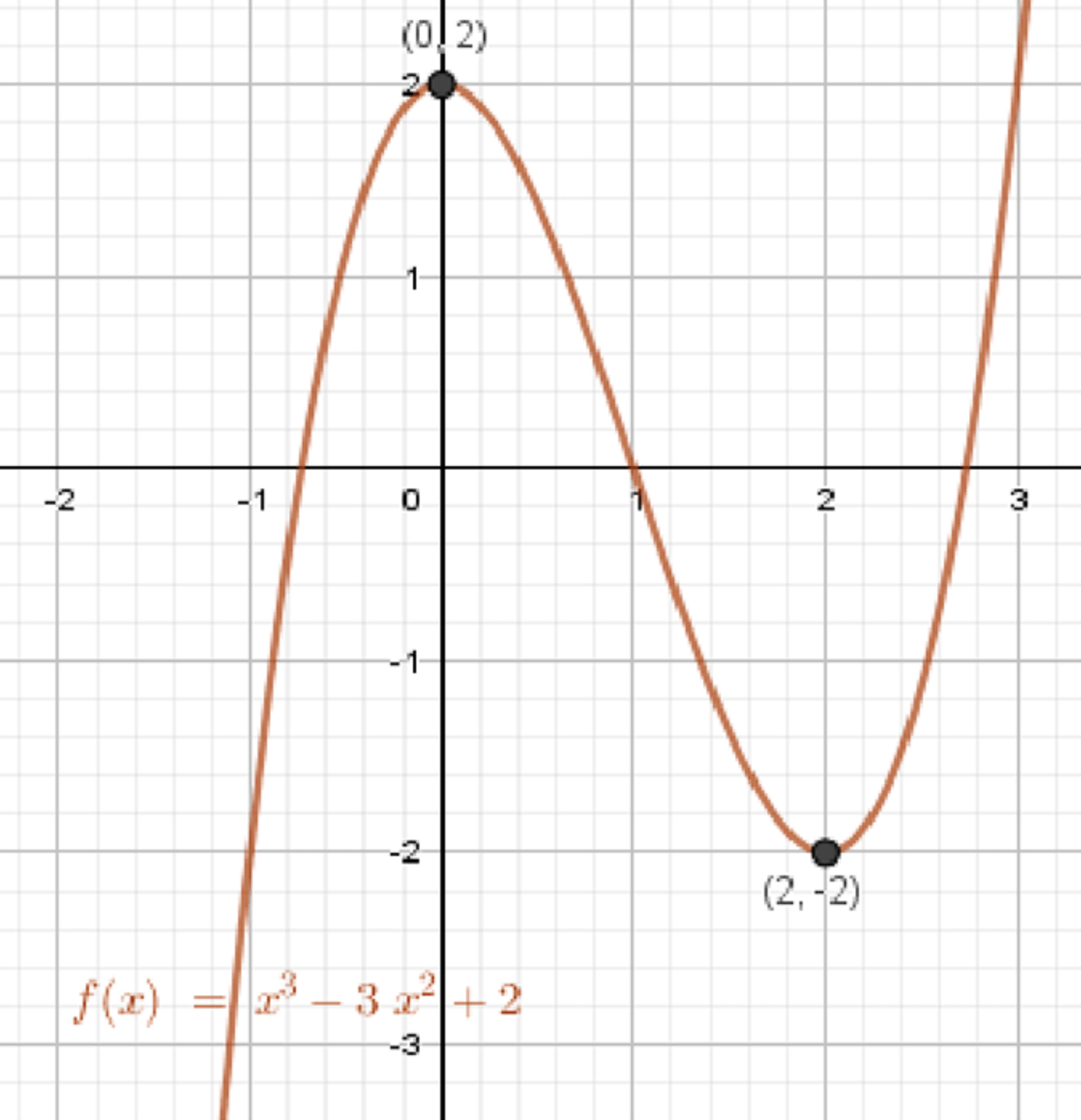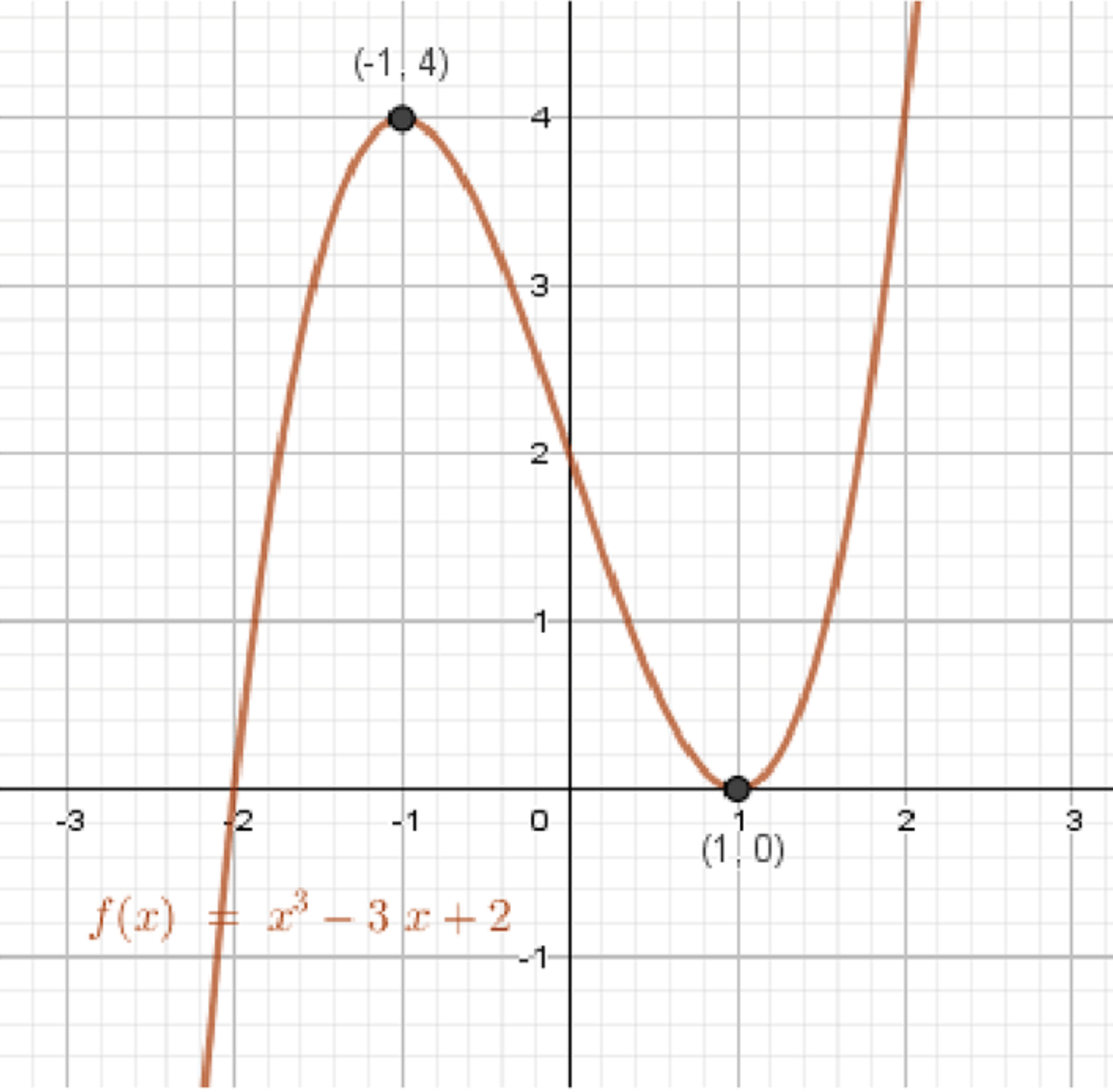Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 31.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а)
б)
в)
г)
Исследовать функцию и построить ее график:
а)
Область определения функции:
Функция не является ни четной, ни нечетной:
У функции отсутствуют асимптоты;
Производная функции:
Промежуток возрастания:
Функция возрастает на ;
Функция убывает на
Координаты некоторых точек:
График функции:
б)
Область определения функции:
Функция не является ни четной, ни нечетной:
У функции отсутствуют асимптоты;
Производная функции:
Промежуток возрастания:
Функция возрастает на ;
Функция убывает на
Координаты некоторых точек:
График функции:
в)
Область определения функции:
Функция не является ни четной, ни нечетной:
У функции отсутствуют асимптоты;
Производная функции:
Промежуток возрастания:
Функция возрастает на ;
Функция убывает на
Координаты некоторых точек:
График функции:
г)
Область определения функции:
Функция не является ни четной, ни нечетной:
У функции отсутствуют асимптоты;
Производная функции:
Промежуток возрастания:
Функция возрастает на ;
Функция убывает на
Координаты некоторых точек:
График функции:
а)
Шаг 1. Область определения (ОДЗ)
Функция является многочленом третьей степени — сумма одночленов. Многочлены определены для любых значений , поэтому:
Ответ:
Шаг 2. Чётность / нечётность
Проверим функцию на чётность/нечётность.
Подставим вместо :
Сравним:
- — функция не чётная
- — функция не нечётная
Вывод:
Функция не является ни чётной, ни нечётной
Шаг 3. Асимптоты
У многочленов:
- нет вертикальных асимптот, потому что функция определена на всей числовой прямой;
- нет горизонтальных асимптот, так как степень числителя больше нуля;
- нет наклонных асимптот, потому что поведение функции на бесконечности задаёт сам многочлен.
Ответ:
Асимптоты отсутствуют
Шаг 4. Найдём производную
Производная нужна для нахождения:
- точек экстремума
- промежутков возрастания и убывания
Функция:
Найдём производную:
Найдём критические точки (где ):
Исследуем знаки производной (метод интервалов)
Разбиваем ось на интервалы:
Проверим знак производной на каждом интервале:
- → возрастает
- → убывает
- → возрастает
Промежутки монотонности:
- на и → возрастает
- на → убывает
Типы критических точек (экстремумы):
- В : производная меняет знак с + на — → максимум
- В : производная меняет знак с — на + → минимум
Шаг 5. Найдём значения функции в точках экстремума
Ответ:
- Максимум в точке
- Минимум в точке
Шаг 6. Промежутки возрастания и убывания
- Возрастание:
- Убывание:
Шаг 7. Вычислим несколько точек для построения графика
Промежуточные вычисления:
Шаг 8. Построение графика (словесное описание)
- Кривая проходит через:
- — максимум
- — минимум
- Слева до — рост
- От до — убывание
- После — снова рост
- Кубическая форма с двумя изгибами (типичная «волна» третьей степени)
Краткий итог по функции :
| Характеристика | Значение |
|---|---|
| Область определения | |
| Чётность | Ни чётная, ни нечётная |
| Асимптоты | Нет |
| Производная | |
| Критические точки | , |
| Максимум | |
| Минимум | |
| Возрастает | |
| Убывает | |
| Точки графика |
б)
Шаг 1. Область определения (ОДЗ)
Функция — это многочлен третьей степени, а многочлены определены на всей числовой прямой.
Ответ:
Шаг 2. Чётность / нечётность
Подставим вместо :
Сравним с :
- → не чётная
- → не нечётная
Вывод:
Функция не является ни чётной, ни нечётной
Шаг 3. Асимптоты
Так как функция является многочленом:
- Нет вертикальных асимптот — функция определена всюду
- Нет горизонтальных и наклонных асимптот — степень числителя больше 1
Ответ:
Асимптоты отсутствуют
Шаг 4. Производная функции
Исходная функция:
Найдём первую производную:
Найдём критические точки (где ):
Анализ производной (знаки)
Рассмотрим интервалы:
Проверим знак :
- На :
→ убывает - На :
→ возрастает - На :
→ убывает
Вывод по производной:
- На : → функция возрастает
- На : → функция убывает
Типы экстремумов:
- : производная меняется с минуса на плюс → минимум
- : производная меняется с плюса на минус → максимум
Шаг 5. Значения функции в экстремумах
Ответ:
- Минимум:
- Максимум:
Шаг 6. Промежутки монотонности
- Возрастание:
- Убывание:
Шаг 7. Точки для построения графика
Подставим значения:
Вычисления:
Шаг 8. Построение графика (словесное описание)
- Кривая проходит через:
- — минимум
- — максимум
- Поведение:
- убывает до
- возрастает на
- убывает после
График имеет S-образную форму, симметричную по расположению максимумов и минимумов.
Краткий итог по функции :
| Характеристика | Значение |
|---|---|
| Область определения | |
| Чётность | Ни чётная, ни нечётная |
| Асимптоты | Отсутствуют |
| Производная | |
| Критические точки | , |
| Минимум | |
| Максимум | |
| Возрастает | |
| Убывает | |
| Точки графика |
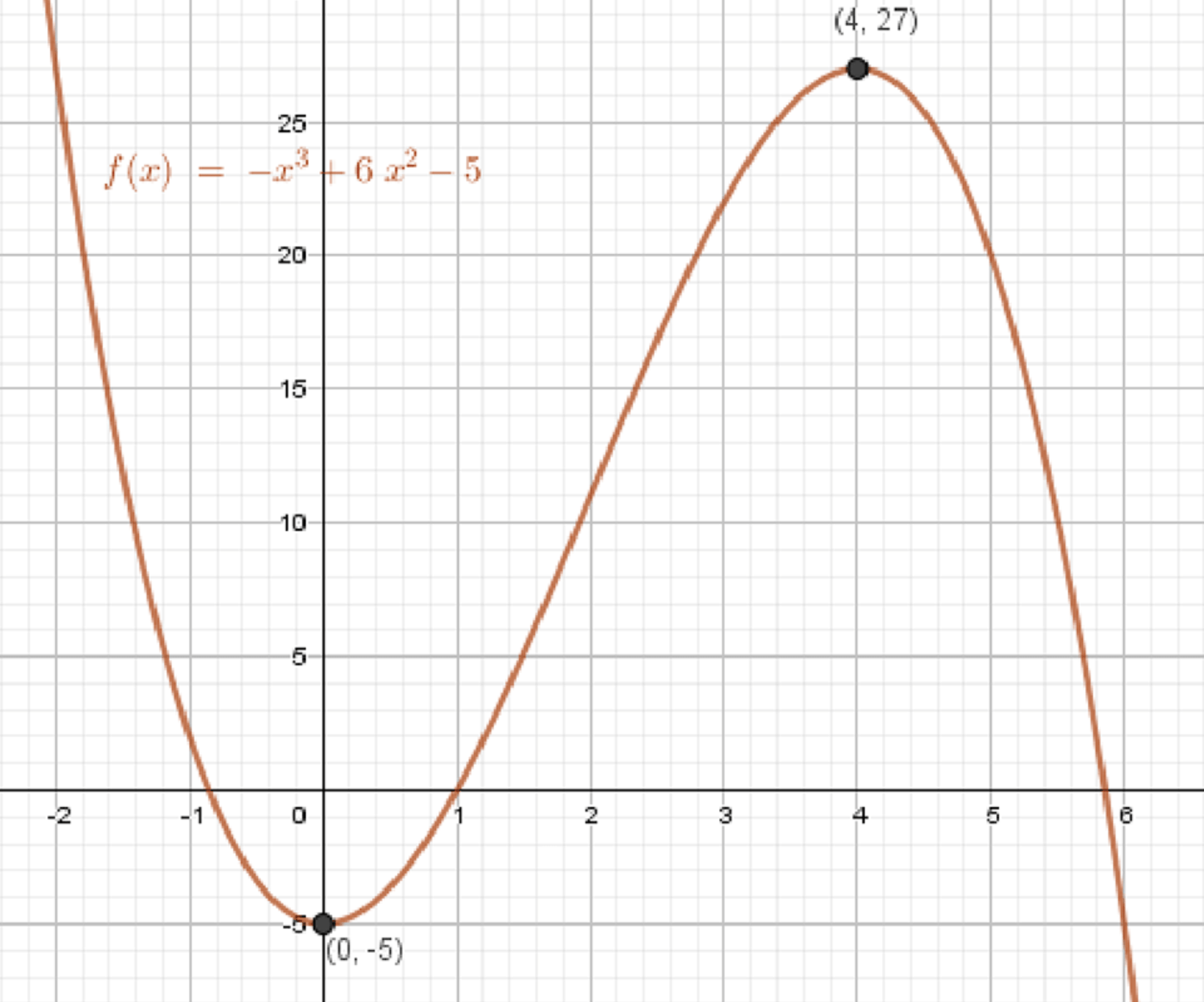
в)
Шаг 1. Область определения (ОДЗ)
Функция — это многочлен третьей степени. Многочлены определены для всех .
Ответ:
Шаг 2. Чётность / нечётность
Подставим вместо :
Сравним:
- — не чётная
- — не нечётная
Вывод:
Функция не является ни чётной, ни нечётной
Шаг 3. Асимптоты
Функция — многочлен, а у многочленов:
- Нет вертикальных асимптот
- Нет горизонтальных асимптот
- Нет наклонных асимптот
Ответ:
Асимптоты отсутствуют
Шаг 4. Производная функции
Исходная функция:
Находим первую производную:
Найдём критические точки (где )
Анализ производной: знаки
Рассмотрим интервалы:
Подставим точки в :
- : → убывает
- : → возрастает
- : → убывает
Вывод по производной:
- Функция убывает на
- Функция возрастает на
- Функция убывает на
Типы точек:
- : производная меняется с минуса на плюс → минимум
- : производная меняется с плюса на минус → максимум
Шаг 5. Значения функции в экстремумах
Ответ:
- Минимум в
- Максимум в
Шаг 6. Промежутки монотонности
- Возрастает на
- Убывает на
Шаг 7. Точки для построения
Подставим:
- :
- :
- :
Таблица:
Шаг 8. Построение графика (словесное описание)
- Кривая проходит через:
- — минимум
- — максимум
- Поведение:
- убывает до
- возрастает от до
- убывает после
- Форма — волнообразная кривая (характерна для кубических функций с двумя экстремумами)
Краткий итог по функции :
| Характеристика | Значение |
|---|---|
| Область определения | |
| Чётность | Ни чётная, ни нечётная |
| Асимптоты | Отсутствуют |
| Производная | |
| Критические точки | , |
| Минимум | |
| Максимум | |
| Возрастает | |
| Убывает | |
| Точки графика |
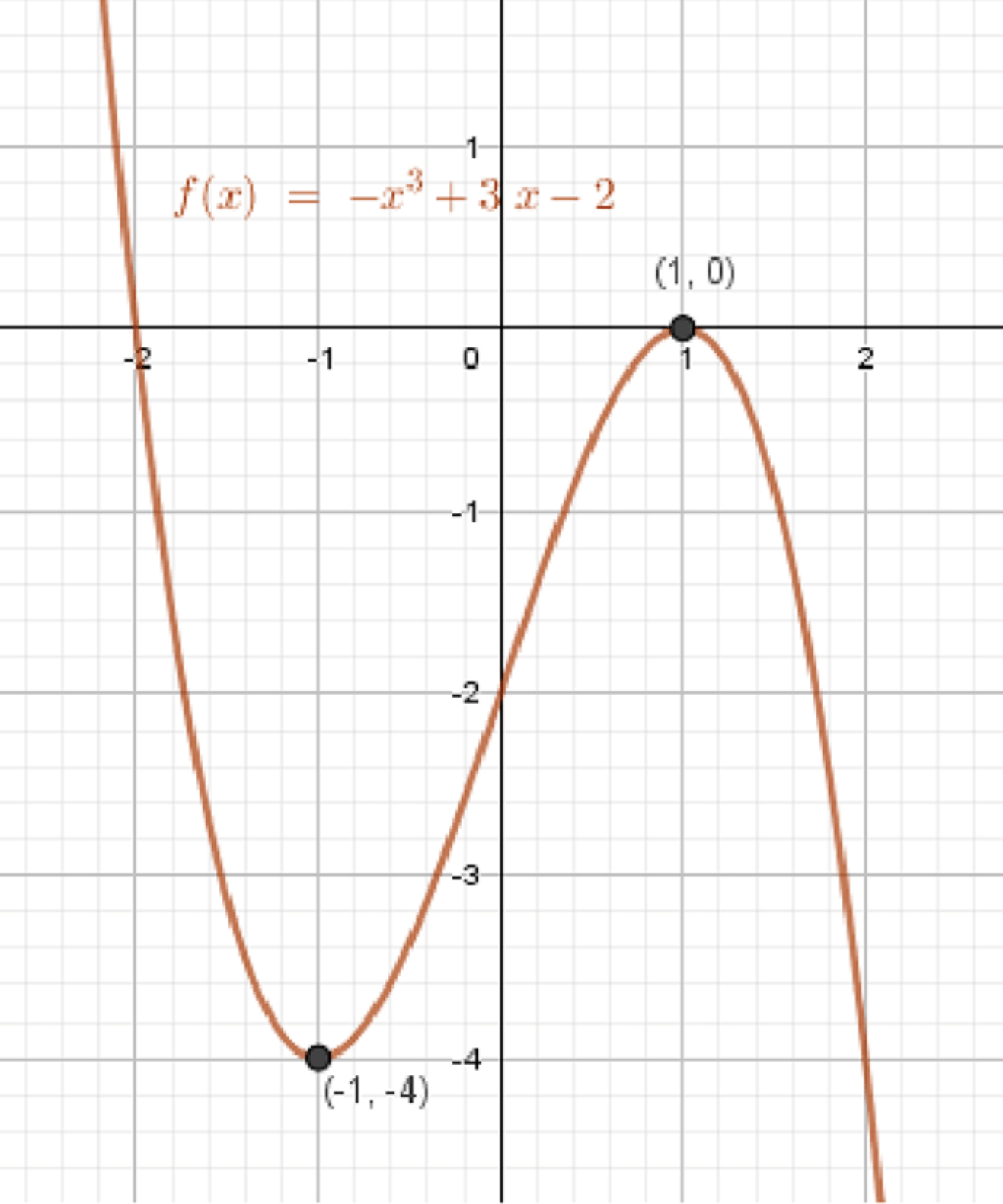
г)
Шаг 1. Область определения (ОДЗ)
Это многочлен третьей степени, а многочлены определены для всех .
Ответ:
Шаг 2. Чётность / нечётность
Проверим функцию на чётность или нечётность.
Сравним:
- — не чётная
- — не нечётная
Вывод:
Функция не является ни чётной, ни нечётной
Шаг 3. Асимптоты
У многочленов:
- нет вертикальных асимптот (везде определены),
- нет горизонтальных асимптот (при , ),
- нет наклонных асимптот (многочлен сам задаёт поведение).
Ответ:
Асимптоты отсутствуют
Шаг 4. Первая производная
Исходная функция:
Находим производную:
Найдём критические точки:
Определим знак производной на интервалах:
Интервалы:
Подставим значения:
- :
→ возрастает - :
→ убывает - :
→ возрастает
Промежутки:
- возрастает на
- убывает на
Типы экстремумов:
- : производная меняется с + на – → максимум
- : производная меняется с – на + → минимум
Шаг 5. Значения функции в экстремумах
Ответ:
- Максимум:
- Минимум:
Шаг 6. Промежутки монотонности
- Возрастает на
- Убывает на
Шаг 7. Точки для построения
Подставим значения:
Вычисления:
Шаг 8. Построение графика (словесно)
- Кривая проходит через:
- — максимум
- — минимум
- Поведение:
- возрастает до
- убывает от до
- затем снова возрастает
- Характерная S-форма графика кубической функции
Краткий итог по функции :
| Характеристика | Значение |
|---|---|
| Область определения | |
| Чётность | Ни чётная, ни нечётная |
| Асимптоты | Отсутствуют |
| Производная | |
| Критические точки | , |
| Максимум | |
| Минимум | |
| Возрастает | |
| Убывает | |
| Точки графика |