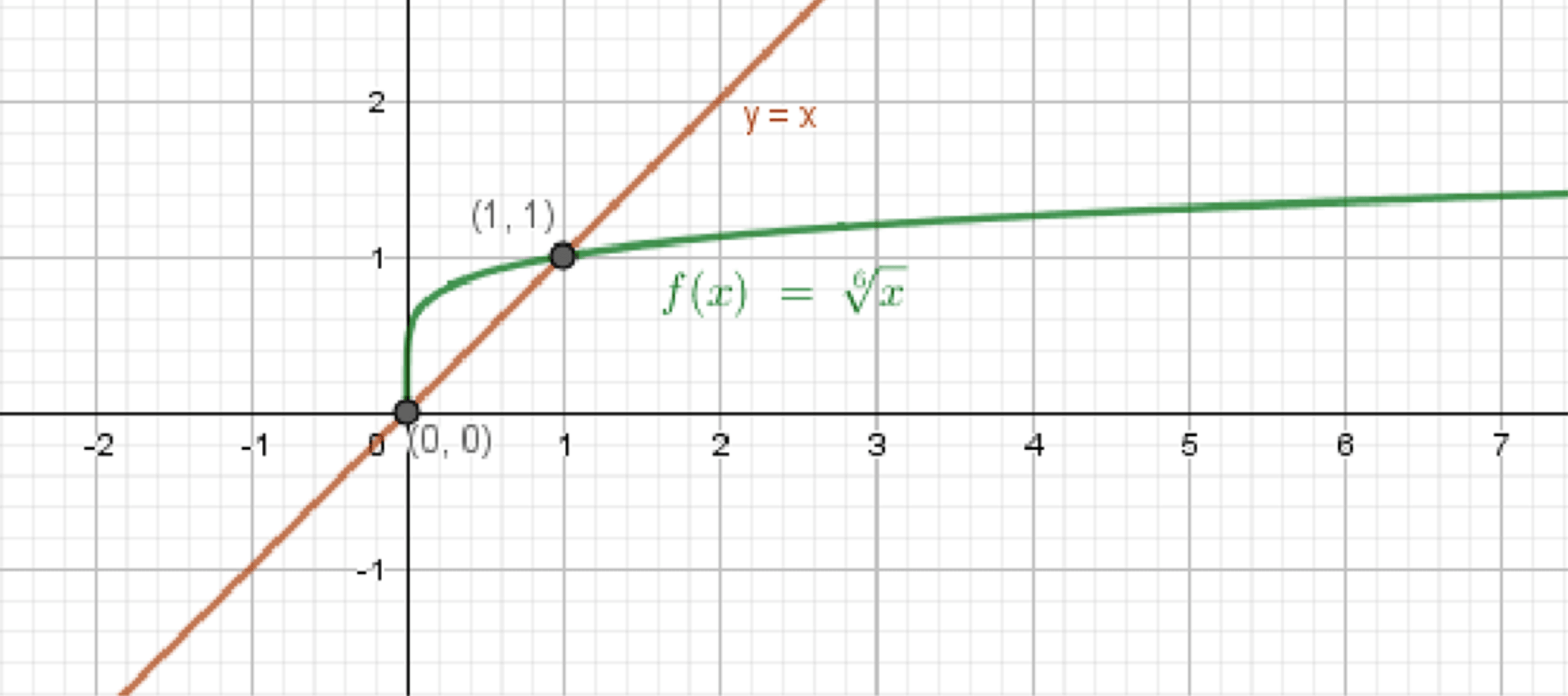Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 34.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Найдите точки пересечения графиков функций:
а) и
б) и
в) и
г) и
Найти точки пересечения графиков функций:
а) и
Графики функций:
Ответ:
б) и
Графики функций:
Ответ:
в) и
Графики функций:
Ответ:
г) и
Графики функций:
Ответ:
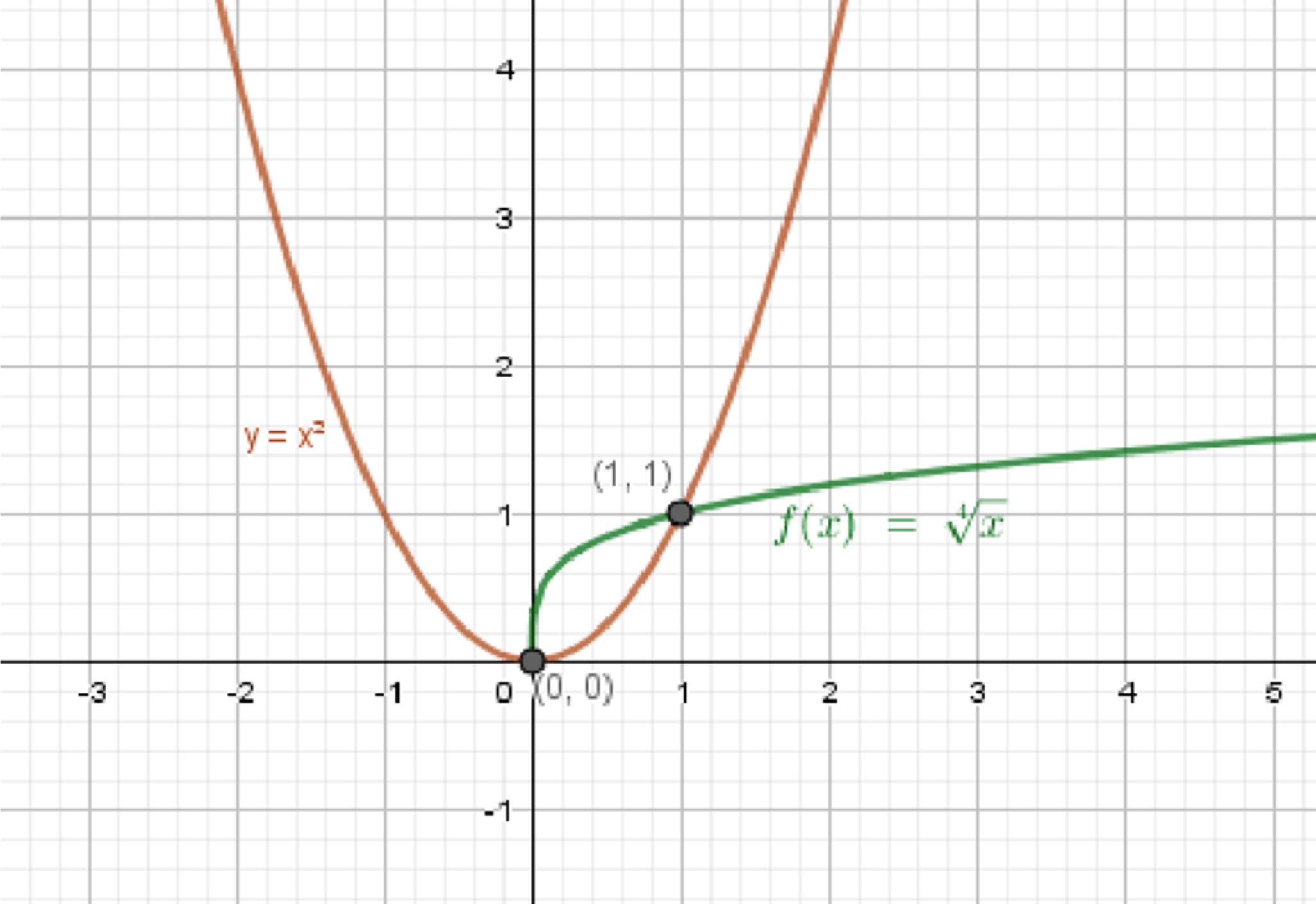
а) и
1. Описание графиков:
— Определён только при (чётный корень).
— Монотонно возрастает.
— Проходит через точку (0; 0), (1; 1), (16; 2).
— Парабола, ветви вверх.
— Определена на всей числовой прямой.
— Проходит через (0; 0), (1; 1), (2; 4), (–1; 1).
2. Приравниваем:
3. Подставим в любую из функций:
Ответ:
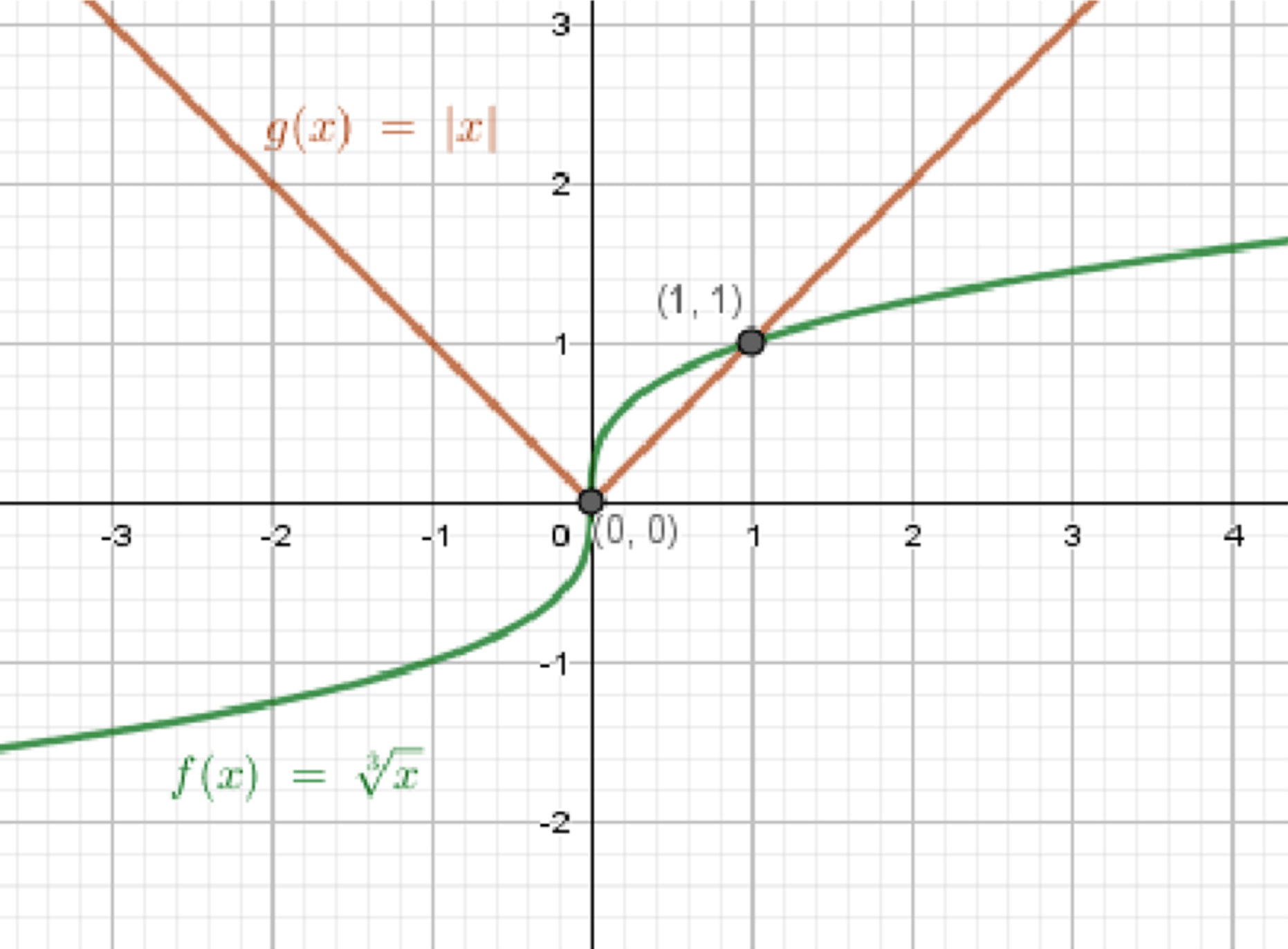
б) и
1. Описание графиков:
— Определён на всей числовой прямой.
— Монотонно возрастает.
— Проходит через (–1; –1), (0; 0), (1; 1)
— Ломаная: при , при
— Проходит через (0; 0), (1; 1), (–1; 1)
2. Приравниваем:
Рассмотрим по областям:
Случай 1:
Случай 2:
Подставим
Значит, пересечений на нет.
Ответ:
в) и
1. Описание графиков:
— Определён при .
— Очень пологая кривая, медленно растущая.
— Проходит через (0; 0), (1; 1)
— Прямая, угол 45°
— Проходит через все точки вида (a; a)
2. Приравниваем:
Для и получаем:
Ответ:
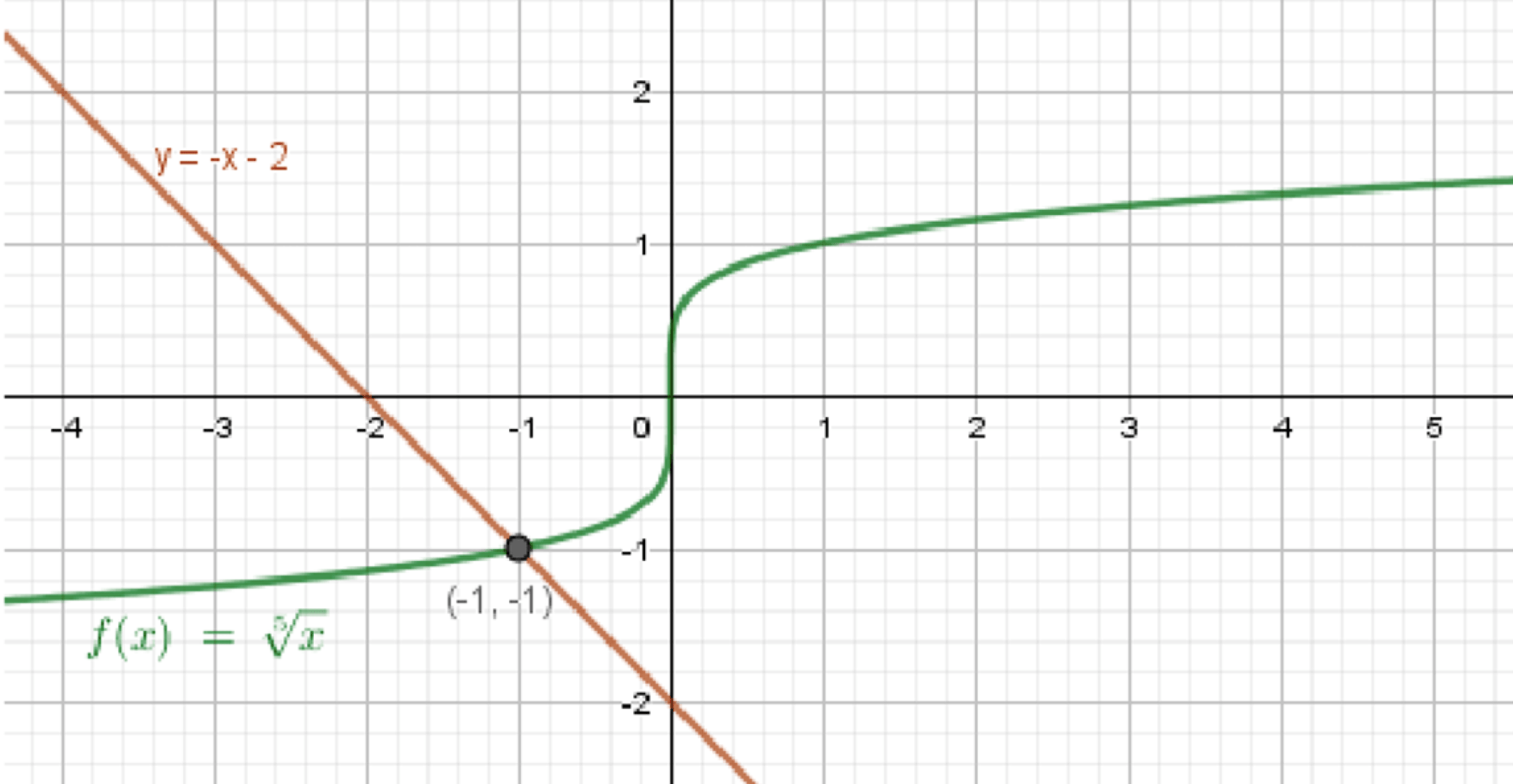
г) и
1. Описание графиков:
— Определён на всей числовой прямой.
— Монотонно возрастает, проходит через (0; 0), (1; 1), (–1; –1)
— Прямая, наклон вниз
— Проходит через (–1; –1), (0; –2), (–2; 0)
2. Приравниваем:
Проверим подстановкой:
Только одна точка пересечения.
Ответ: