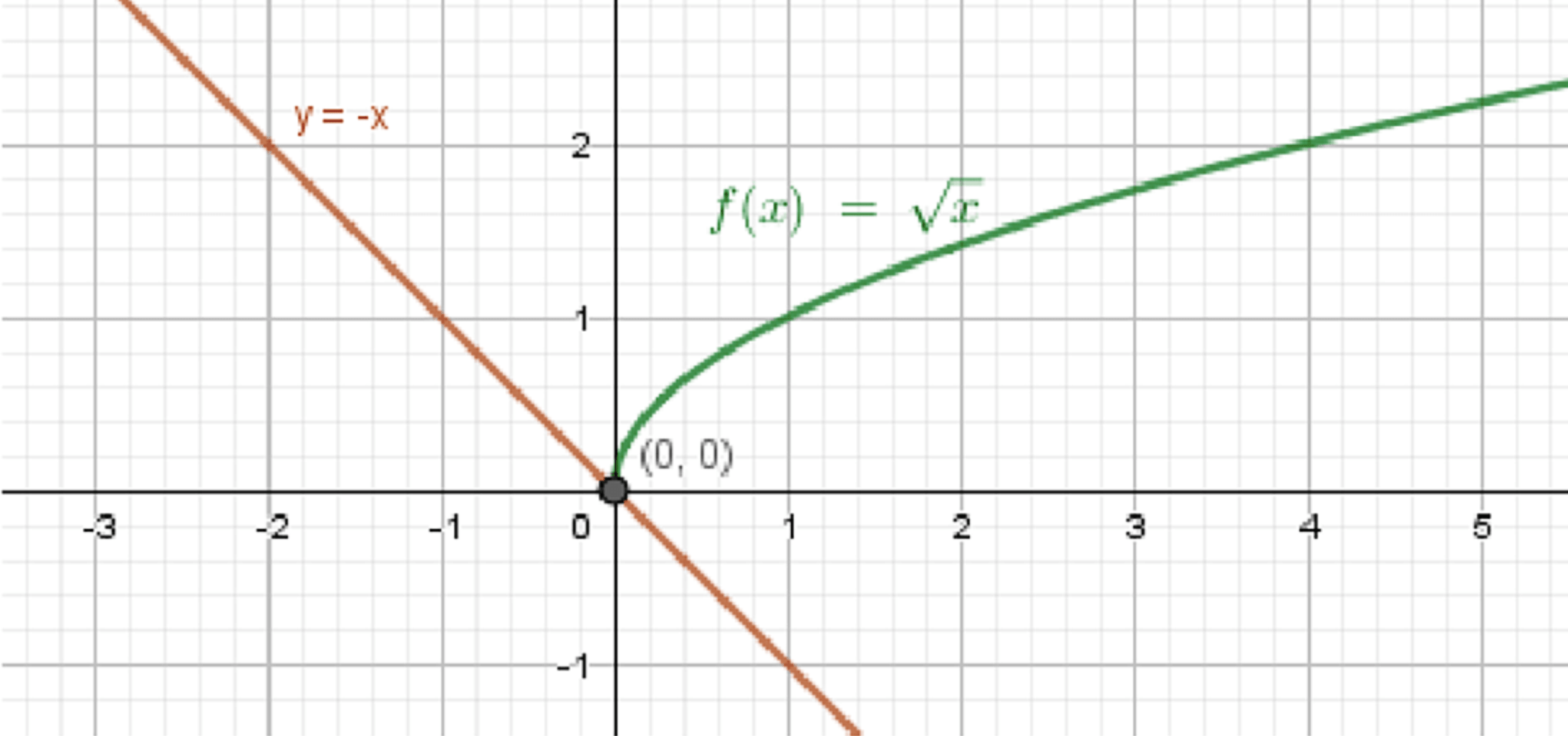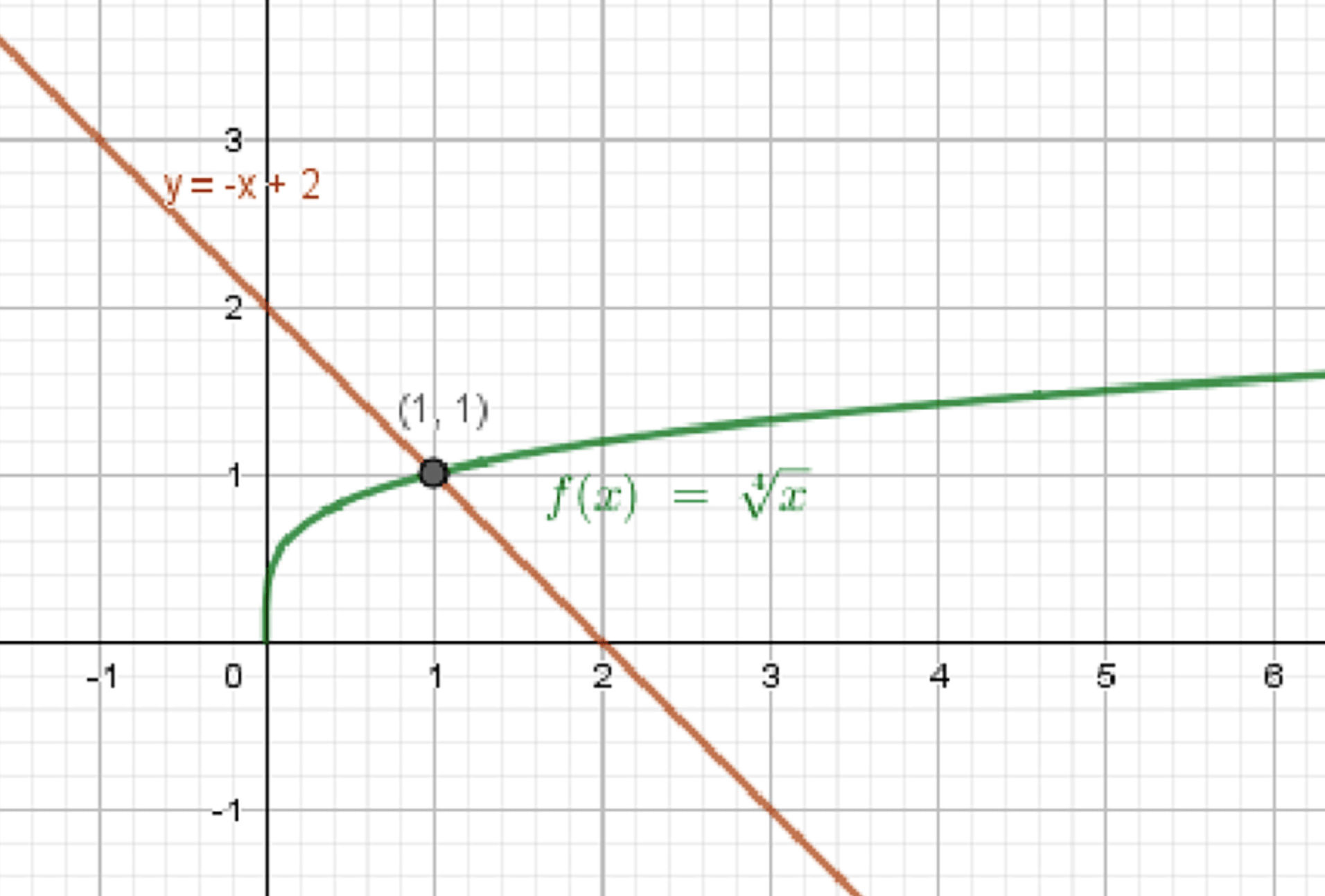Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 34.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а)
б)
в)
г)
Решить графически уравнение:
а)
Графики функций:
Ответ:
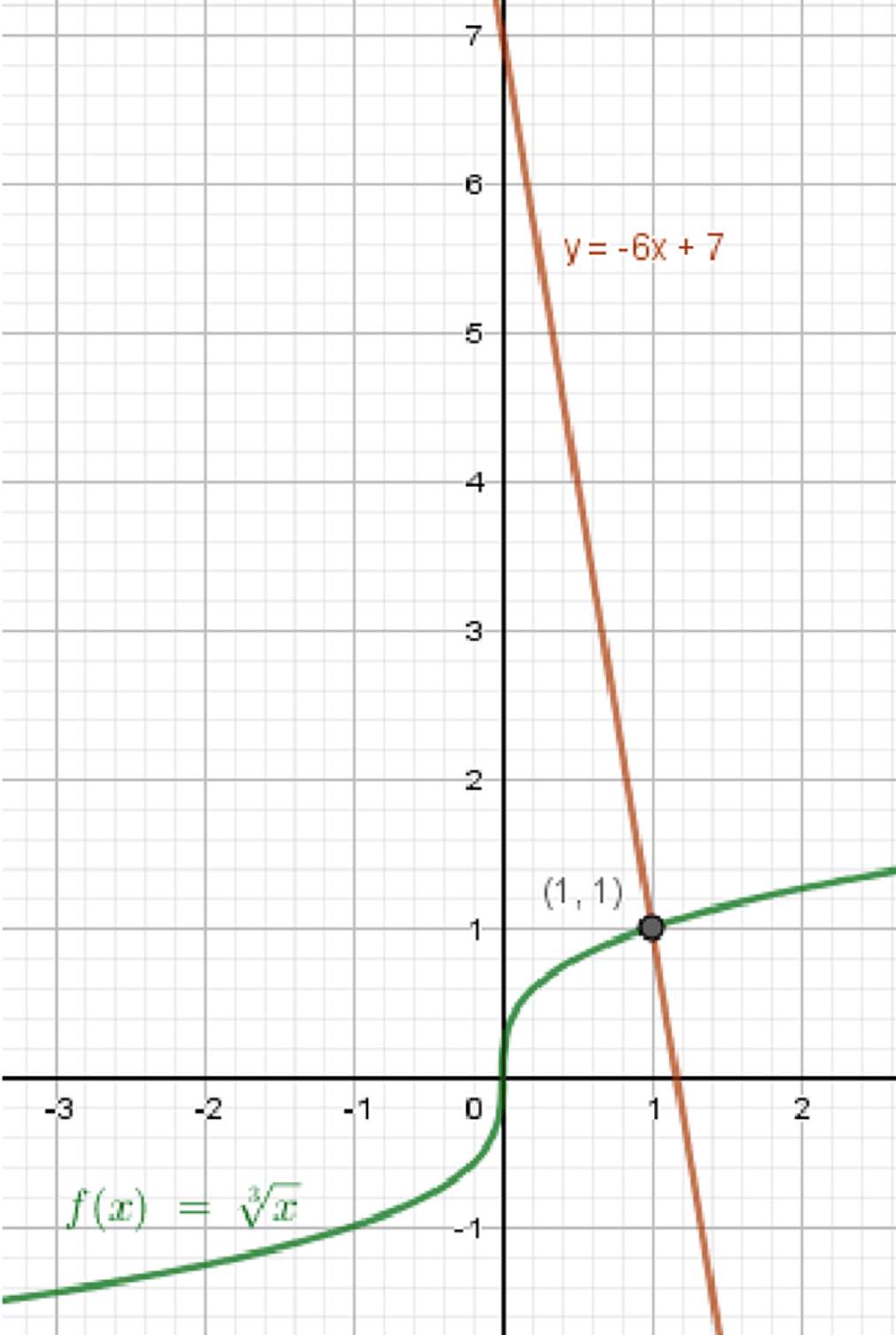
б)
Графики функций:
Ответ:
в)
Графики функций:
Ответ:
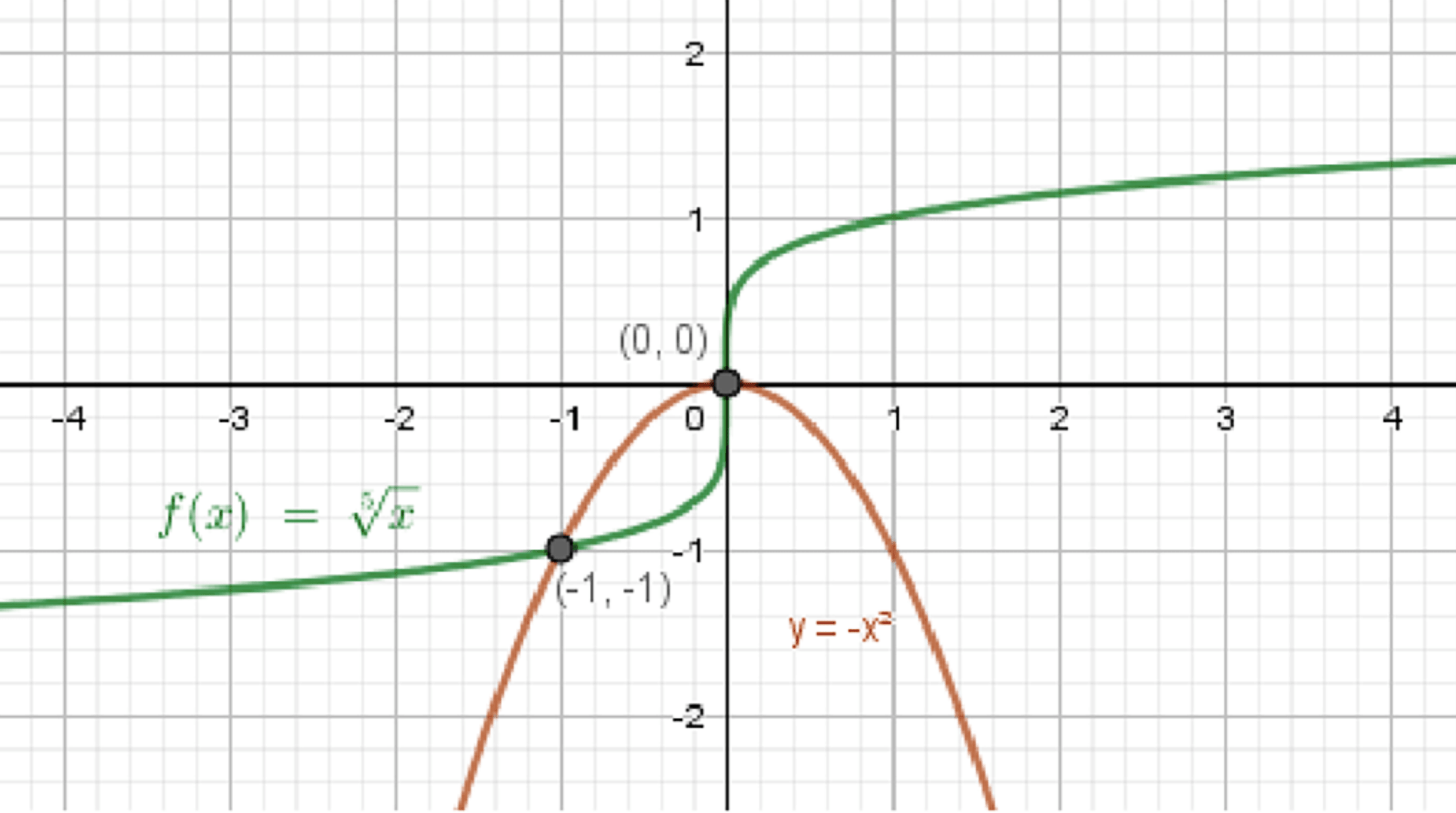
г)
Графики функций:
Ответ:
а)
Шаг 1. Области определения
- определена при
- определена при всех
Общая область определения:
Шаг 2. Исследование знаков
- при
Следовательно:
Проверим:
- Подставим :
→ равенство выполняется.
Других решений нет, потому что:
- Левая часть неотрицательная
- Правая часть неположительная
- При : , но → противоречие
Ответ:
б)
Шаг 1. Области определения
- : определена при всех
- : определена при всех
Общая область определения:
Шаг 2. Приравниваем
Эта функция аналитически трудно решается, но можно подбором:
Проверим :
Проверим, есть ли другие:
- возрастает медленно
- — линейно убывает быстро
→ значит, пересекаются только один раз
Ответ:
в)
Шаг 1. Области определения
- определена при
- : определена при всех
Общая область:
Шаг 2. Приравниваем:
Проверим несколько значений:
- : → не равно
- : → подходит
- : → не равно
Обе функции возрастают и убывают соответственно, пересекаются только в одной точке.
Ответ:
г)
Шаг 1. Области определения
- : определена при всех
- : определена при всех
Общая область:
Шаг 2. Приравниваем:
Рассмотрим несколько значений:
Исследование:
- Левая часть — возрастает, от до
- Правая часть — убывает в обе стороны от нуля
→ Пересечение максимум в двух точках
Ответ:
Финальные ответы:
а)
б)
в)
г)