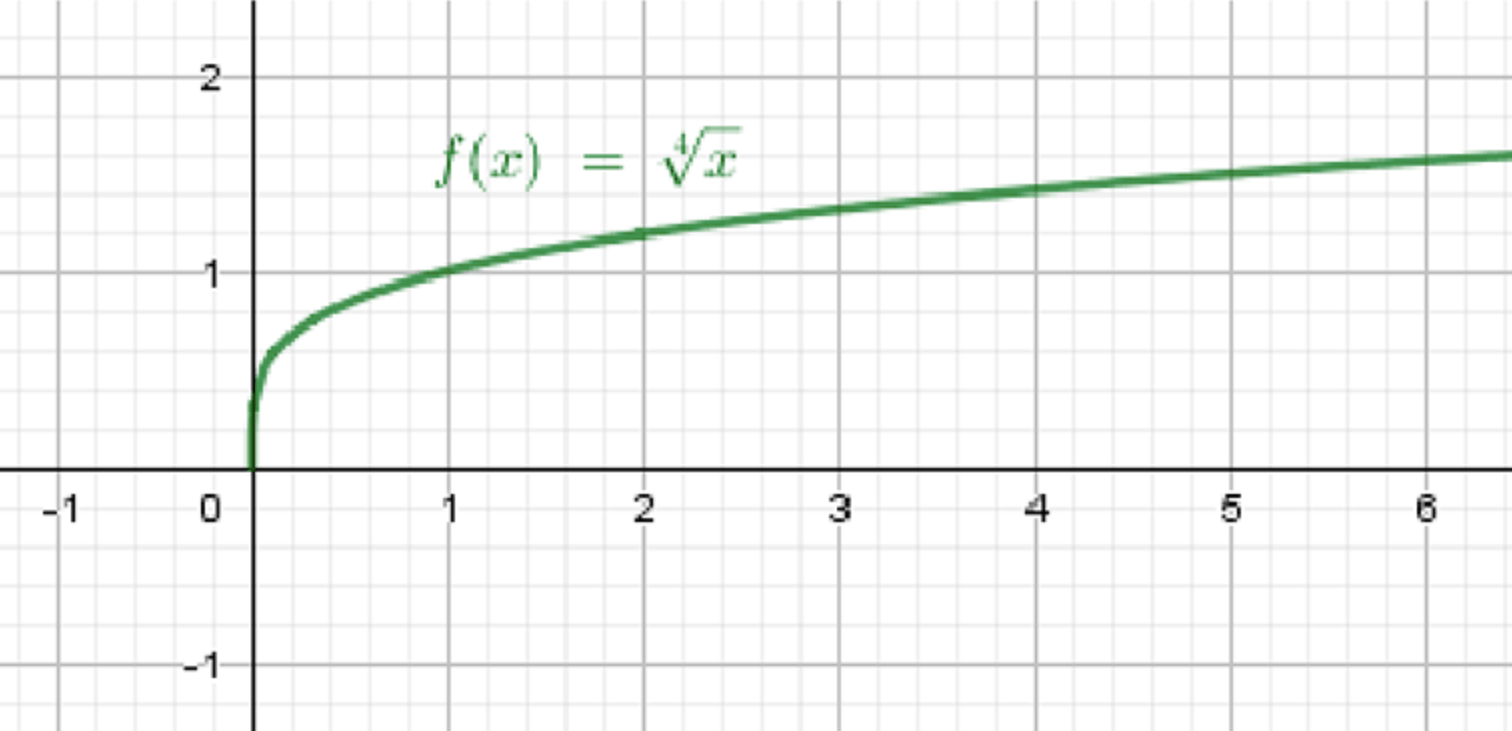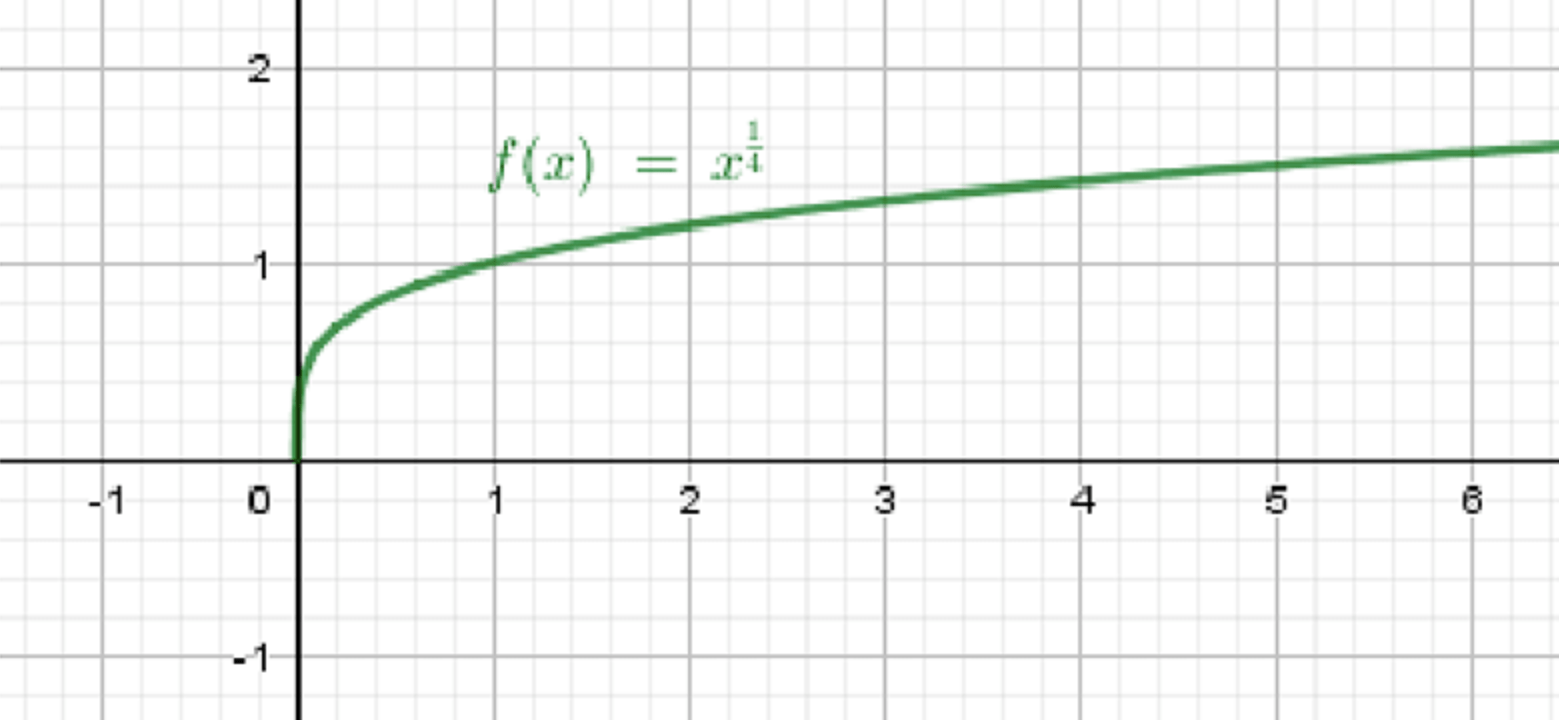Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 38.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте и сравните графики функций:
а) и ;
б) и
Построить и сравнить графики функций:
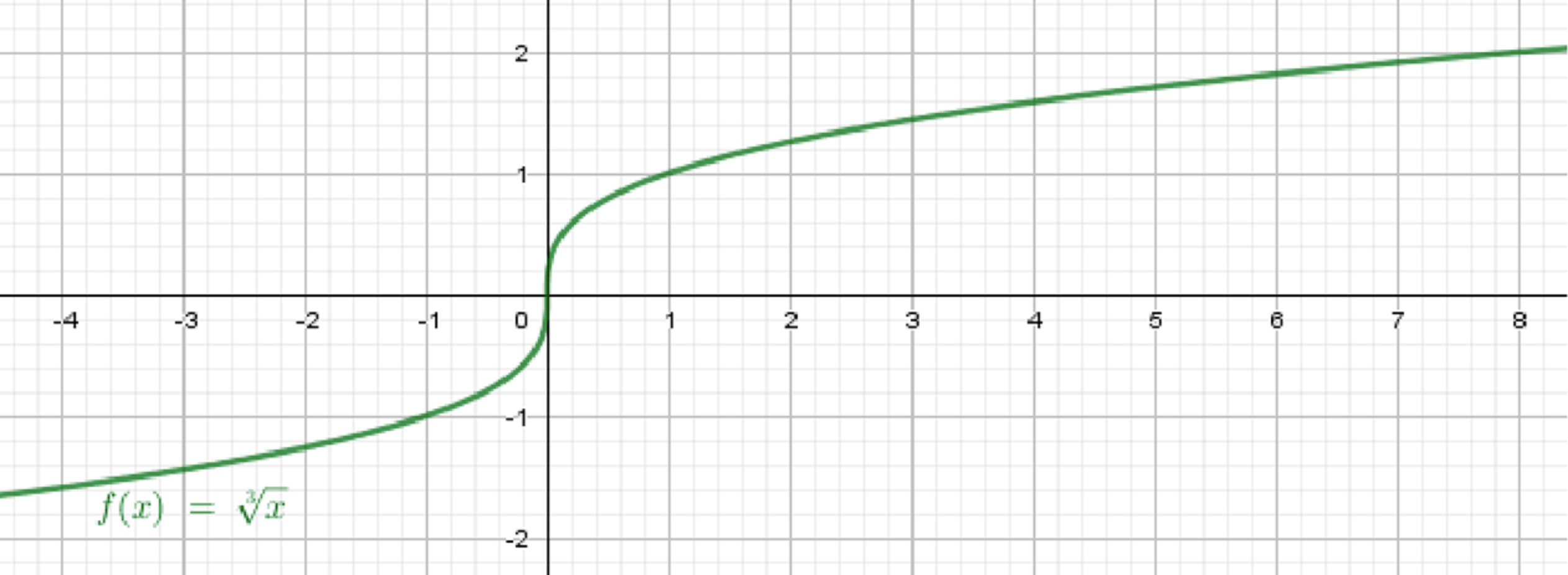
а) и ;
График функции :
График функции :
Графики совпадают на луче ;
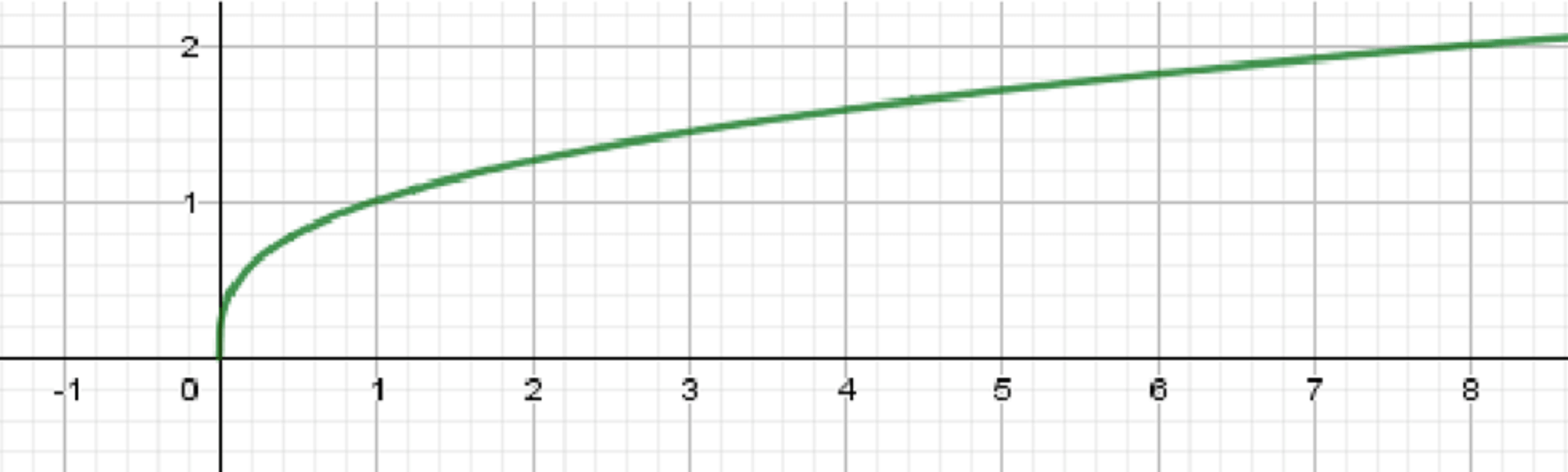
б) и ;
График функции :
График функции :
Графики полностью совпадают
а) и
1. Аналитическое выражение
Функции записаны в двух эквивалентных формах:
- — корневая запись
- — степенная запись
Это — одна и та же функция, так как:
2. Область определения
Корень нечётной степени (в данном случае — кубический корень) определён при любых действительных значениях .
Вывод:
3. Поведение функции
Функция обладает следующими свойствами:
- Нечётная функция:
Следовательно, график симметричен относительно начала координат.
- Монотонность:
Функция монотонно возрастает на всей области определения. - Кривизна (выпуклость):
- Для : функция выпуклая вниз.
- Для : функция выпуклая вверх.
- Значения функции:
4. Сравнение графиков
- Формулы и задают одну и ту же функцию.
- Следовательно, графики полностью совпадают на всей области определения: .
- Примечание: В исходном тексте указано, что графики совпадают на луче . Это некорректно, потому что функции равны также и при отрицательных значениях . Видимо, ошибка или опечатка.
б) и
1. Аналитическое выражение
Формулы:
- — корневая форма (четвёртый корень из )
- — степенная форма (четвёртая степень корня)
Они обозначают одну и ту же функцию, так как:
2. Область определения
Корень чётной степени (в данном случае — четвёртой степени) определён только при неотрицательных значениях .
Вывод:
3. Поведение функции
Функция обладает следующими свойствами:
- Функция нечётная не является, так как область определения не симметрична.
- Монотонность:
Функция возрастает на всей области определения. - Кривизна (выпуклость):
Функция выпуклая вверх на . - Значения функции:
0 1 16 0 1 2 - Поведение функции:
- Медленно растёт, особенно на больших значениях .
- При ,
- При , , но очень медленно
4. Сравнение графиков
- Обе записи задают одну и ту же функцию
- Области определения совпадают:
- Графики полностью совпадают
- График начинается в точке (0;0), медленно поднимается вверх, является вогнутой кривой (выпуклой вверх)