Задача
Решите графически уравнение:
а) log 2 x = − x + 1 \log_2 x = -x + 1
б) log 1 3 x = 2 x − 2 \log_{\frac{1}{3}} x = 2x — 2
в) log 9 x = − x + 1 \log_9 x = -x + 1
г) log 7 3 x = 4 x − 4 \log_{\frac{7}{3}} x = 4x — 4
Краткий ответ:
Решить графически уравнение:
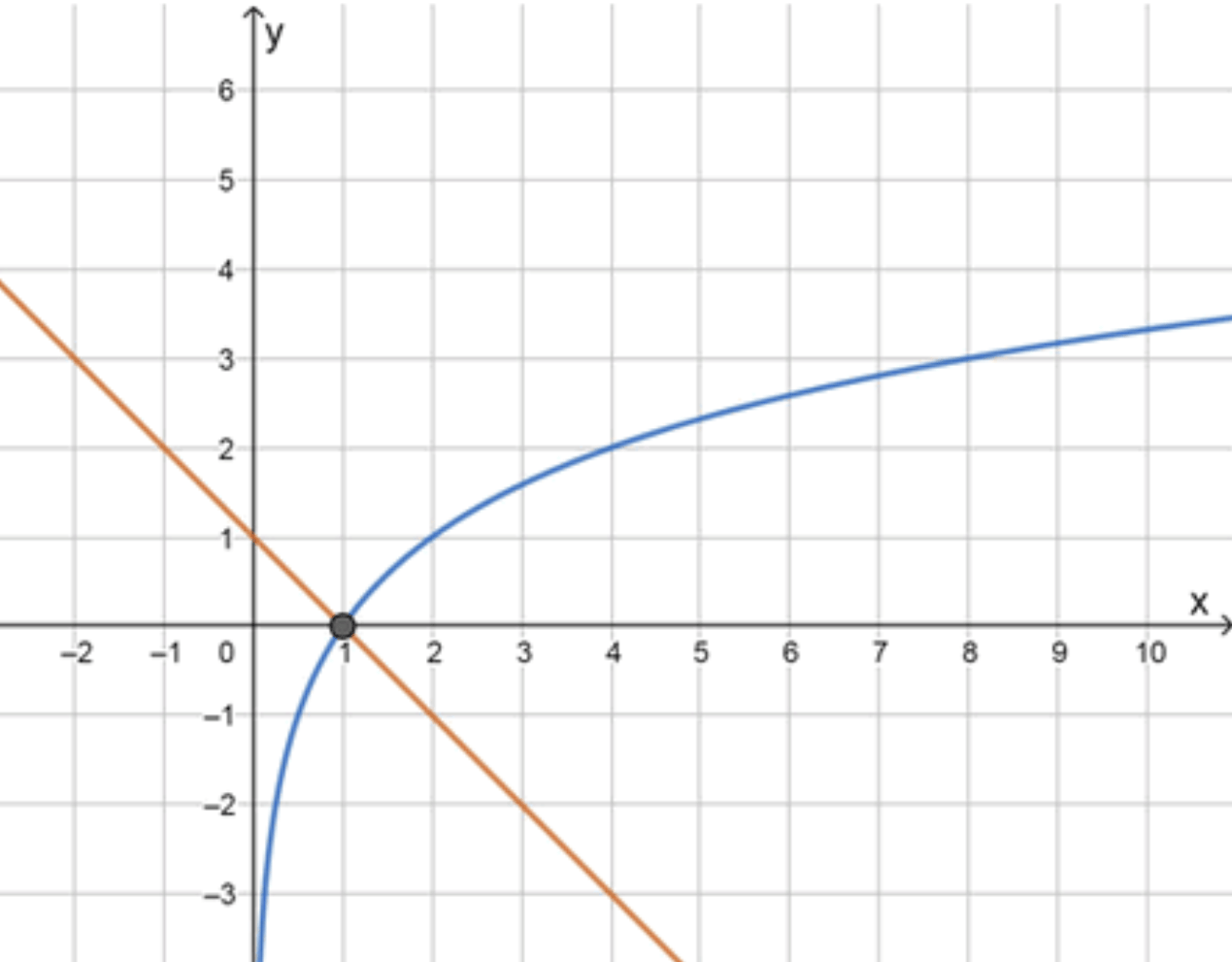
а) log 2 x = − x + 1 \log_2 x = -x + 1 y = log 2 x y = \log_2 x
x 1 4 8 y 0 2 3 \begin{array}{|c|c|c|c|} \hline x & 1 & 4 & 8 \\ \hline y & 0 & 2 & 3 \\ \hline \end{array}
y = − x + 1 y = -x + 1
x 0 1 y 1 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 1 & 0 \\ \hline \end{array}
Графики функций:
Ответ: 1.
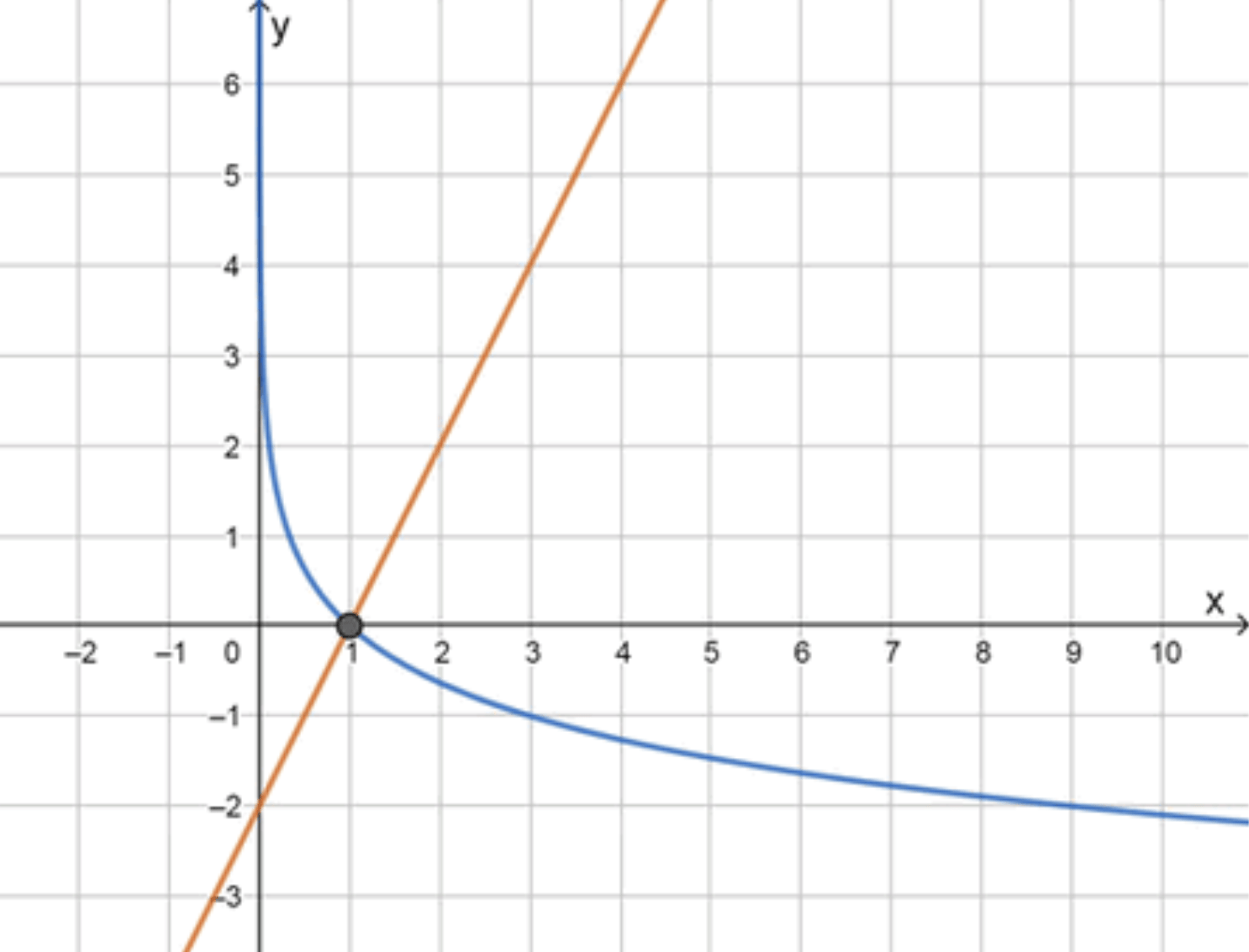
б) log 1 3 x = 2 x − 2 \log_{\frac{1}{3}} x = 2x — 2 y = log 1 3 x y = \log_{\frac{1}{3}} x
x 1 3 9 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = 2 x − 2 y = 2x — 2
x 0 1 y − 2 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & -2 & 0 \\ \hline \end{array}
Графики функций:
Ответ: 1.
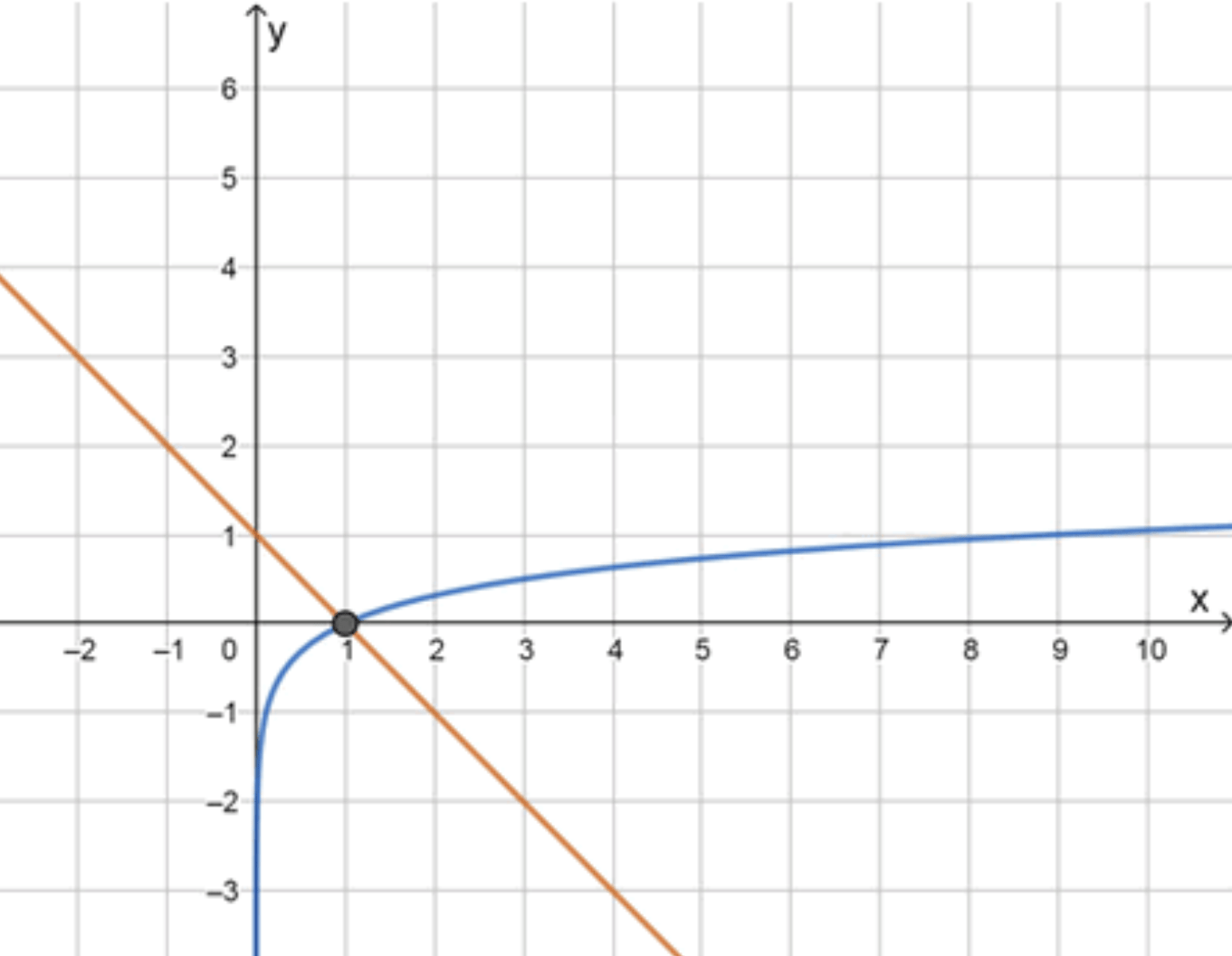
в) log 9 x = − x + 1 \log_9 x = -x + 1 y = log 9 x y = \log_9 x
x 1 3 9 y 0 0,5 1 \begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & 0{,}5 & 1 \\ \hline \end{array}
y = − x + 1 y = -x + 1
x 0 1 y 1 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 1 & 0 \\ \hline \end{array}
Графики функций:
Ответ: 1.
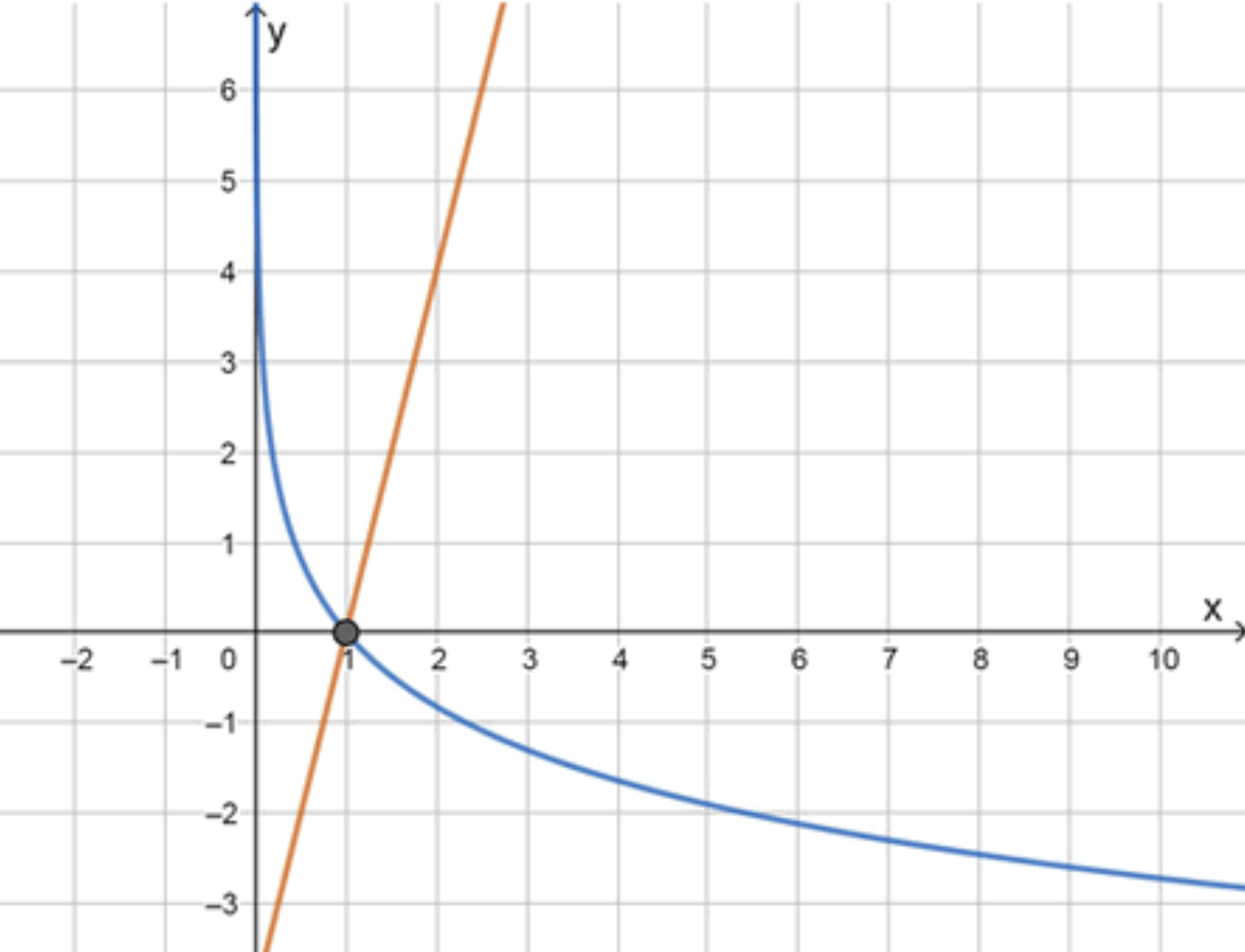
г) log 7 3 x = 4 x − 4 \log_{\frac{7}{3}} x = 4x — 4 y = log 7 3 x y = \log_{\frac{7}{3}} x
x 1 2 1 3 5 4 9 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 2\frac{1}{3} & 5\frac{4}{9} \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = 4 x − 4 y = 4x — 4
x 0 1 y − 4 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & -4 & 0 \\ \hline \end{array}
Графики функций:
Ответ: 1.
Подробный ответ:
а) Уравнение:
log 2 x = − x + 1 \log_2 x = -x + 1
Шаг 1: Область определения
Логарифм определён при x > 0 x > 0 Уравнение имеет смысл только при x ∈ ( 0 ; + ∞ ) x \in (0; +\infty) Шаг 2: Построение графика y = log 2 x y = \log_2 x
Это логарифмическая функция с основанием 2 > 1 2 > 1 возрастает на ( 0 ; + ∞ ) (0; +\infty) Значения: x y = log 2 x 1 0 4 2 8 3 \begin{array}{|c|c|} \hline x & y = \log_2 x \\ \hline 1 & 0 \\ 4 & 2 \\ 8 & 3 \\ \hline \end{array}
Дополнительно:log 2 2 = 1 \log_2 2 = 1 log 2 1 2 = − 1 \log_2 \frac{1}{2} = -1 Шаг 3: Построение графика y = − x + 1 y = -x + 1
Линейная функция: убывает, так как коэффициент при x x − 1 -1 Значения: x y = − x + 1 0 1 1 0 \begin{array}{|c|c|} \hline x & y = -x + 1 \\ \hline 0 & 1 \\ 1 & 0 \\ \hline \end{array}
Прямая проходит через точки ( 0 ; 1 ) (0; 1) ( 1 ; 0 ) (1; 0) Шаг 4: Поиск точки пересечения
Сравним:log 2 1 = 0 \log_2 1 = 0 − 1 + 1 = 0 -1 + 1 = 0 x = 1 x = 1 → Единственная общая точка: x = 1 x = 1
Шаг 5: Проверка графически
Графики пересекаются в точке ( 1 ; 0 ) (1; 0) До и после этой точки:log 2 x \log_2 x − x + 1 -x + 1
Ответ:
1 \boxed{1}
б) Уравнение:
log 1 3 x = 2 x − 2 \log_{\frac{1}{3}} x = 2x — 2
Шаг 1: ОДЗ
Шаг 2: График y = log 1 3 x y = \log_{\frac{1}{3}} x
Основание 1 3 ∈ ( 0 ; 1 ) \frac{1}{3} \in (0; 1) убывает Значения: x y = log 1 3 x 1 0 3 − 1 9 − 2 \begin{array}{|c|c|} \hline x & y = \log_{\frac{1}{3}} x \\ \hline 1 & 0 \\ 3 & -1 \\ 9 & -2 \\ \hline \end{array}
Дополнительно:log 1 3 1 3 = 1 \log_{\frac{1}{3}} \frac{1}{3} = 1 При x → 0 + x \to 0^+ y → + ∞ y \to +\infty Шаг 3: График y = 2 x − 2 y = 2x — 2
Прямая, возрастает , так как коэффициент при x x Значения: x y = 2 x − 2 0 − 2 1 0 \begin{array}{|c|c|} \hline x & y = 2x — 2 \\ \hline 0 & -2 \\ 1 & 0 \\ \hline \end{array}
Шаг 4: Поиск точки пересечения
Проверим x = 1 x = 1 log 1 3 1 = 0 \log_{\frac{1}{3}} 1 = 0 2 ⋅ 1 − 2 = 0 2 \cdot 1 — 2 = 0 → Обе функции равны при x = 1 x = 1
Шаг 5: Проверка поведения функций
log 1 3 x \log_{\frac{1}{3}} x 2 x − 2 2x — 2 одна точка пересечения
Ответ:
1 \boxed{1}
в) Уравнение:
log 9 x = − x + 1 \log_9 x = -x + 1
Шаг 1: ОДЗ
Шаг 2: График y = log 9 x y = \log_9 x
Основание 9 > 1 9 > 1 возрастает Значения: x y = log 9 x 1 0 3 0.5 9 1 \begin{array}{|c|c|} \hline x & y = \log_9 x \\ \hline 1 & 0 \\ 3 & 0.5 \\ 9 & 1 \\ \hline \end{array}
При x → 0 + x \to 0^+ y → − ∞ y \to -\infty Шаг 3: График y = − x + 1 y = -x + 1
x y = − x + 1 0 1 1 0 \begin{array}{|c|c|} \hline x & y = -x + 1 \\ \hline 0 & 1 \\ 1 & 0 \\ \hline \end{array}
Шаг 4: Точка пересечения
Проверим x = 1 x = 1 log 9 1 = 0 \log_9 1 = 0 − 1 + 1 = 0 -1 + 1 = 0 → Пересекаются в точке x = 1 x = 1
Шаг 5: Поведение функций
log 9 x \log_9 x − x + 1 -x + 1 единственная точка пересечения
Ответ:
1 \boxed{1}
г) Уравнение:
log 7 3 x = 4 x − 4 \log_{\frac{7}{3}} x = 4x — 4
Шаг 1: ОДЗ
Шаг 2: График y = log 7 3 x y = \log_{\frac{7}{3}} x
Основание 7 3 > 1 \frac{7}{3} > 1 возрастает Значения: x y = log 7 3 x 1 0 2 1 3 − 1 5 4 9 − 2 \begin{array}{|c|c|} \hline x & y = \log_{\frac{7}{3}} x \\ \hline 1 & 0 \\ 2\frac{1}{3} & -1 \\ 5\frac{4}{9} & -2 \\ \hline \end{array}
При x → 0 + x \to 0^+ y → − ∞ y \to -\infty Шаг 3: График y = 4 x − 4 y = 4x — 4
Прямая, возрастает быстро Значения: x y = 4 x − 4 0 − 4 1 0 \begin{array}{|c|c|} \hline x & y = 4x — 4 \\ \hline 0 & -4 \\ 1 & 0 \\ \hline \end{array}
Шаг 4: Проверка пересечения
Проверим x = 1 x = 1 log 7 3 1 = 0 \log_{\frac{7}{3}} 1 = 0 4 ⋅ 1 − 4 = 0 4 \cdot 1 — 4 = 0 → Пересекаются в точке x = 1 x = 1
Шаг 5: Поведение
Обе функции возрастают, но log 7 3 x \log_{\frac{7}{3}} x медленно ,4 x − 4 4x — 4 быстро , поэтому пересекаются только один раз
Ответ:
1