Краткий ответ:
Решить графически неравенство:
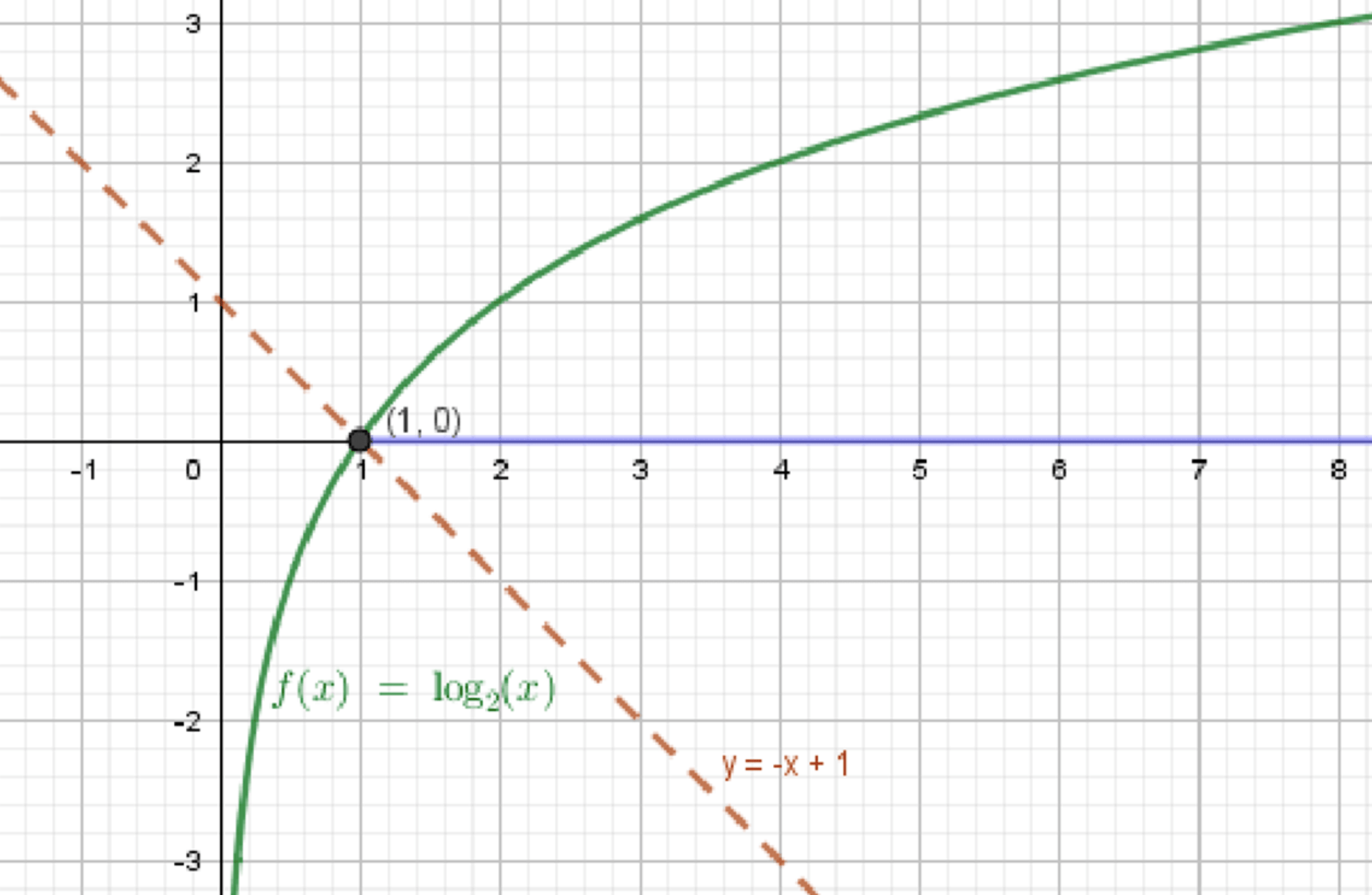
а) log 2 x ≥ − x + 1 \log_2 x \ge -x + 1 y = log 2 x y = \log_2 x
x 1 4 8 y 0 2 3 \begin{array}{|c|c|c|c|} \hline x & 1 & 4 & 8 \\ \hline y & 0 & 2 & 3 \\ \hline \end{array}
y = − x + 1 y = -x + 1
x 0 1 y 1 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 1 & 0 \\ \hline \end{array}
Графики функций:
Ответ: x ∈ [ 1 ; + ∞ ) x \in [1; +\infty)
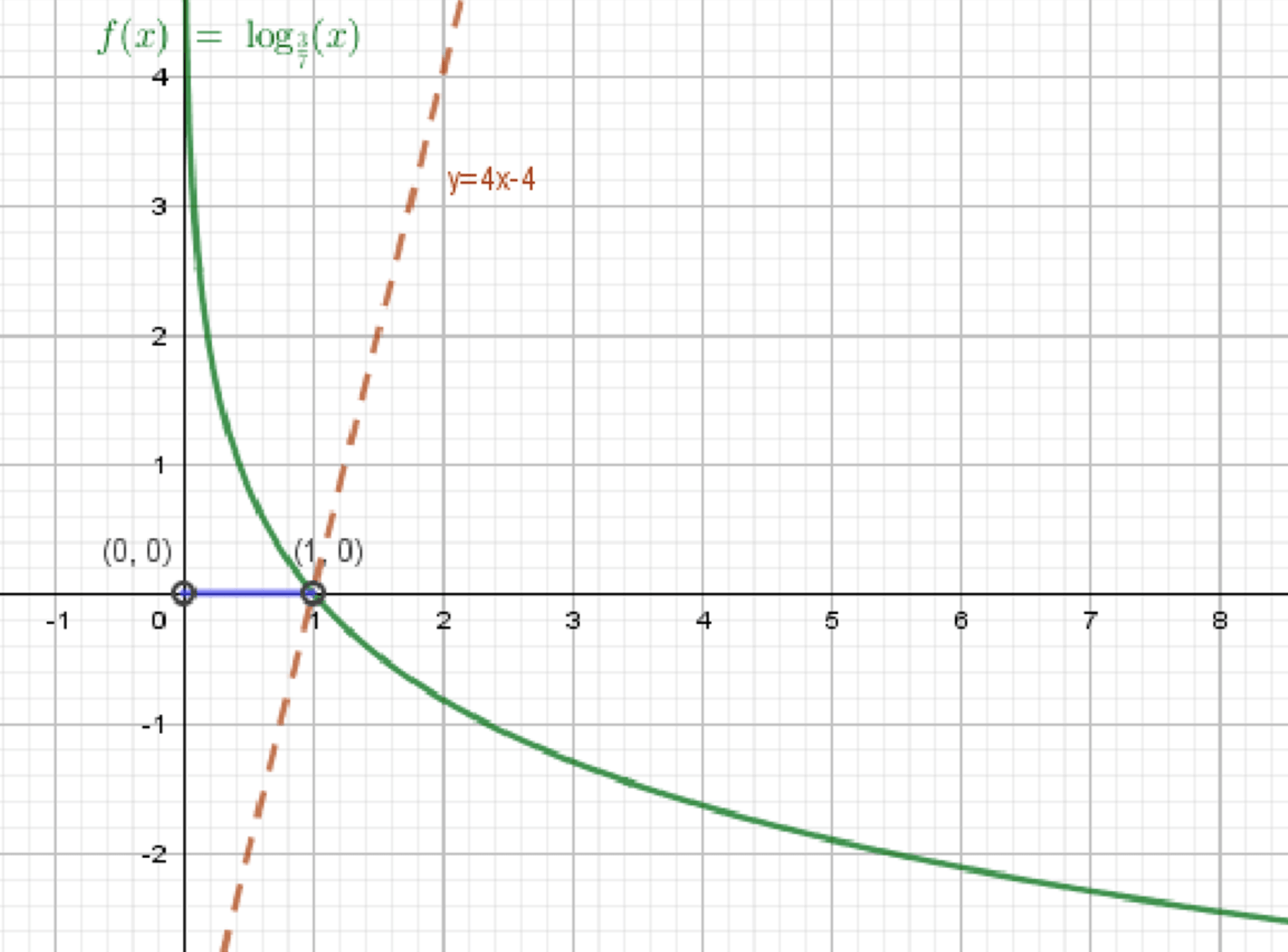
б) log 7 3 x > 4 x − 4 \log_{\frac{7}{3}} x > 4x — 4 y = log 7 3 x y = \log_{\frac{7}{3}} x
x 1 2 1 3 5 4 9 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 2\frac{1}{3} & 5\frac{4}{9} \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = 4 x − 4 y = 4x — 4
x 0 1 y − 4 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & -4 & 0 \\ \hline \end{array}
Графики функций:
Ответ: x ∈ ( 0 ; 1 ) x \in (0; 1)
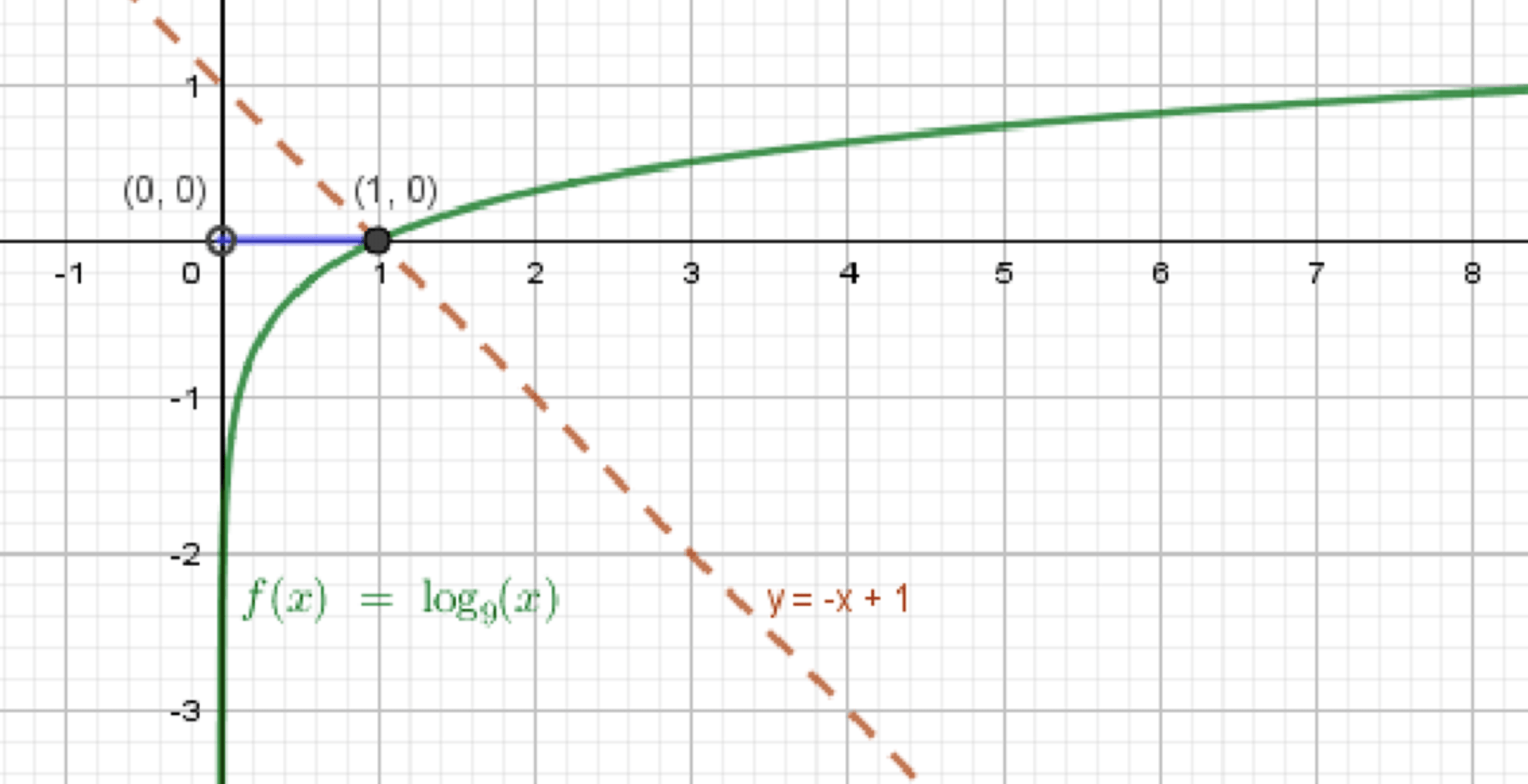
в) log 9 x ≤ − x + 1 \log_9 x \le -x + 1 y = log 9 x y = \log_9 x
x 1 3 9 y 0 0,5 1 \begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & 0{,}5 & 1 \\ \hline \end{array}
y = − x + 1 y = -x + 1
x 0 1 y 1 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 1 & 0 \\ \hline \end{array}
Графики функций:
Ответ: x ∈ ( 0 ; 1 ] x \in (0; 1]
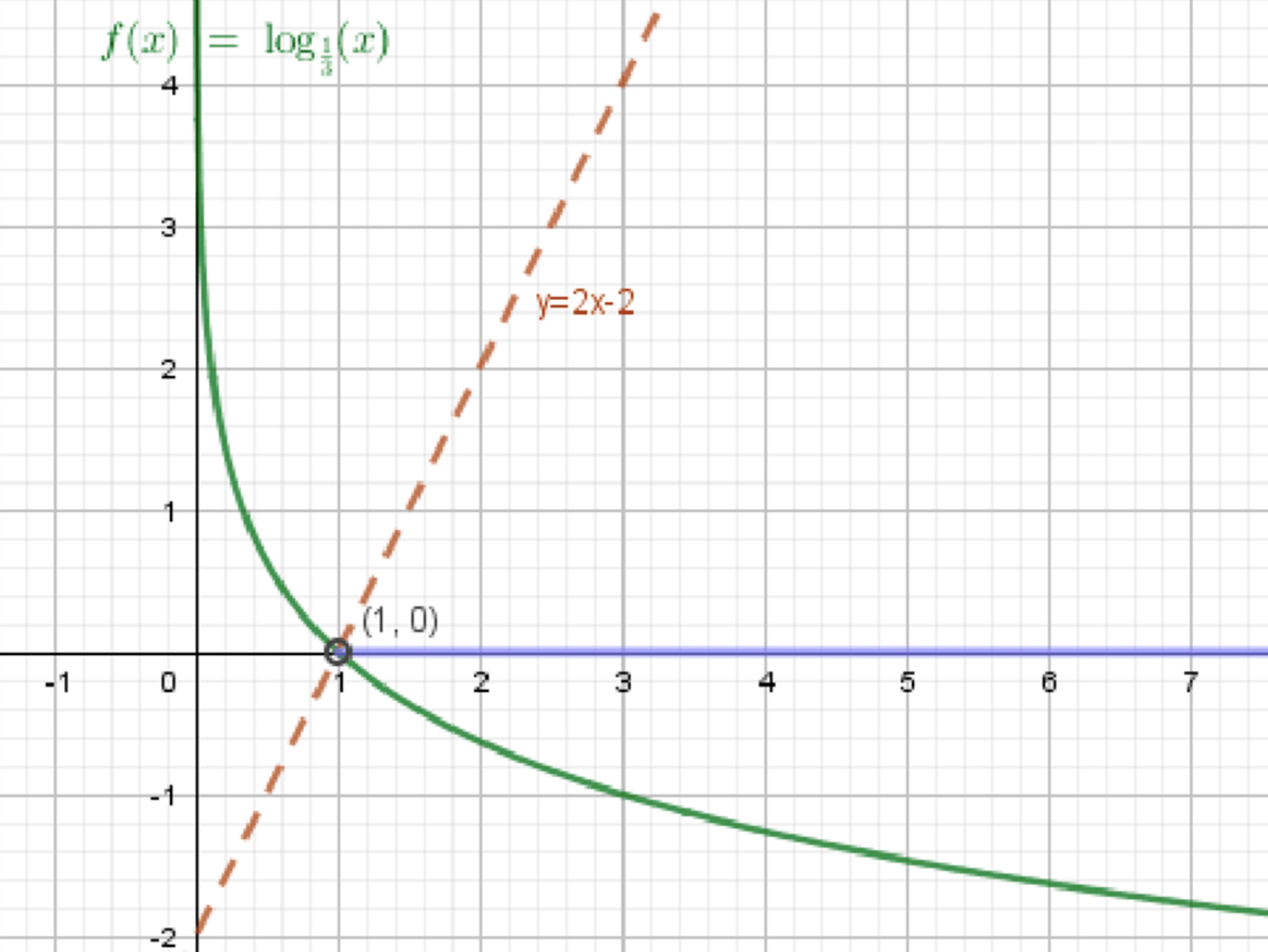
г) log 1 3 x < 2 x − 2 \log_{\frac{1}{3}} x < 2x — 2 y = log 1 3 x y = \log_{\frac{1}{3}} x
x 1 3 9 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = 2 x − 2 y = 2x — 2
x 0 1 y − 2 0 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & -2 & 0 \\ \hline \end{array}
Графики функций:
Ответ: x ∈ ( 1 ; + ∞ ) x \in (1; +\infty)
Подробный ответ:
а) Решить неравенство:
log 2 x ≥ − x + 1 \log_2 x \geq -x + 1
Шаг 1. Определим область определения.
Логарифм log 2 x \log_2 x
x > 0 x > 0
Шаг 2. Построим график функции y = log 2 x y = \log_2 x
Функция возрастает, так как основание логарифма больше 1.
x log 2 x 1 0 4 2 8 3 \begin{array}{|c|c|} \hline x & \log_2 x \\ \hline 1 & 0 \\ 4 & 2 \\ 8 & 3 \\ \hline \end{array}
Также:
При x → 0 + x \to 0^+ y → − ∞ y \to -\infty При x → + ∞ x \to +\infty y → + ∞ y \to +\infty Шаг 3. Построим график y = − x + 1 y = -x + 1
Это уравнение прямой с наклоном вниз.
x y 0 1 1 0 \begin{array}{|c|c|} \hline x & y \\ \hline 0 & 1 \\ 1 & 0 \\ \hline \end{array}
Шаг 4. Найдём точку пересечения графиков.
При x = 1 x = 1
log 2 1 = 0 , − 1 + 1 = 0 ⇒ точка пересечения: ( 1 ; 0 ) \log_2 1 = 0,\quad -1 + 1 = 0 \Rightarrow \text{точка пересечения: } (1; 0)
Шаг 5. Определим, где логарифм больше или равен прямой.
Для x < 1 x < 1 log 2 x < − x + 1 \log_2 x < -x + 1 Для x = 1 x = 1 log 2 x = − x + 1 \log_2 x = -x + 1 Для x > 1 x > 1 log 2 x > − x + 1 \log_2 x > -x + 1 Шаг 6. Учитываем ОДЗ x > 0 x > 0
x ∈ [ 1 ; + ∞ ) x \in [1; +\infty)
Ответ:
x ∈ [ 1 ; + ∞ ) x \in [1; +\infty)
б) Решить неравенство:
log 7 3 x > 4 x − 4 \log_{\frac{7}{3}} x > 4x — 4
Шаг 1. ОДЗ
x > 0 x > 0
Шаг 2. Построим y = log 7 3 x y = \log_{\frac{7}{3}} x
Так как основание 7 3 > 1 \frac{7}{3} > 1
x y 1 0 2,33 − 1 5,44 − 2 \begin{array}{|c|c|} \hline x & y \\ \hline 1 & 0 \\ 2{,}33 & -1 \\ 5{,}44 & -2 \\ \hline \end{array}
→ На первых участках значения убывают, значит масштаб логарифма слабый.
Шаг 3. Построим y = 4 x − 4 y = 4x — 4
Прямая, круто возрастает.
x = 0 ⇒ y = − 4 ; x = 1 ⇒ y = 0 x = 0 \Rightarrow y = -4;\quad x = 1 \Rightarrow y = 0
Шаг 4. Найдём точку пересечения
При x = 1 x = 1
log 7 3 1 = 0 ; 4 ⋅ 1 − 4 = 0 \log_{\frac{7}{3}} 1 = 0;\quad 4 \cdot 1 — 4 = 0
→ Пересекаются в точке ( 1 ; 0 ) (1; 0)
Шаг 5. Сравниваем значения
Для x < 1 x < 1 Для x > 1 x > 1 Итог:
x ∈ ( 0 ; 1 ) x \in (0; 1)
Ответ:
x ∈ ( 0 ; 1 ) x \in (0; 1)
в) Решить неравенство:
log 9 x ≤ − x + 1 \log_9 x \leq -x + 1
Шаг 1. ОДЗ
x > 0 x > 0
Шаг 2. y = log 9 x y = \log_9 x
Основание 9 > 1 9 > 1
x y 1 0 3 0,5 9 1 \begin{array}{|c|c|} \hline x & y \\ \hline 1 & 0 \\ 3 & 0{,}5 \\ 9 & 1 \\ \hline \end{array}
Шаг 3. Прямая y = − x + 1 y = -x + 1
x = 0 ⇒ y = 1 ; x = 1 ⇒ y = 0 x = 0 \Rightarrow y = 1;\quad x = 1 \Rightarrow y = 0
→ Прямая убывает
Шаг 4. Точка пересечения
При x = 1 x = 1
log 9 1 = 0 ; − 1 + 1 = 0 ⇒ пересекаются \log_9 1 = 0;\quad -1 + 1 = 0 \Rightarrow \text{пересекаются}
Шаг 5. Сравнение
Для x < 1 x < 1 Для x > 1 x > 1 Итог:
Неравенство выполняется при:
x ∈ ( 0 ; 1 ] x \in (0; 1]
Ответ:
x ∈ ( 0 ; 1 ] x \in (0; 1]
г)
Решить неравенство:
log 1 3 x < 2 x − 2 \log_{\frac{1}{3}} x < 2x — 2
Шаг 1. ОДЗ
x > 0 x > 0
Шаг 2. y = log 1 3 x y = \log_{\frac{1}{3}} x
Основание меньше 1 ⇒ функция убывает
x y 1 0 3 − 1 9 − 2 \begin{array}{|c|c|} \hline x & y \\ \hline 1 & 0 \\ 3 & -1 \\ 9 & -2 \\ \hline \end{array}
Шаг 3. Прямая y = 2 x − 2 y = 2x — 2
x = 0 ⇒ y = − 2 ; x = 1 ⇒ y = 0 x = 0 \Rightarrow y = -2;\quad x = 1 \Rightarrow y = 0
Прямая возрастает.
Шаг 4. Точка пересечения
При x = 1 x = 1
log 1 3 1 = 0 ; 2 ⋅ 1 − 2 = 0 \log_{\frac{1}{3}} 1 = 0;\quad 2 \cdot 1 — 2 = 0
→ Пересечение в точке ( 1 ; 0 ) (1; 0)
Шаг 5. Сравнение
Для x < 1 x < 1 Для x > 1 x > 1 Итог:
x ∈ ( 1 ; + ∞ ) x \in (1; +\infty)
Ответ:
x ∈ ( 1 ; + ∞ ) x \in (1; +\infty)