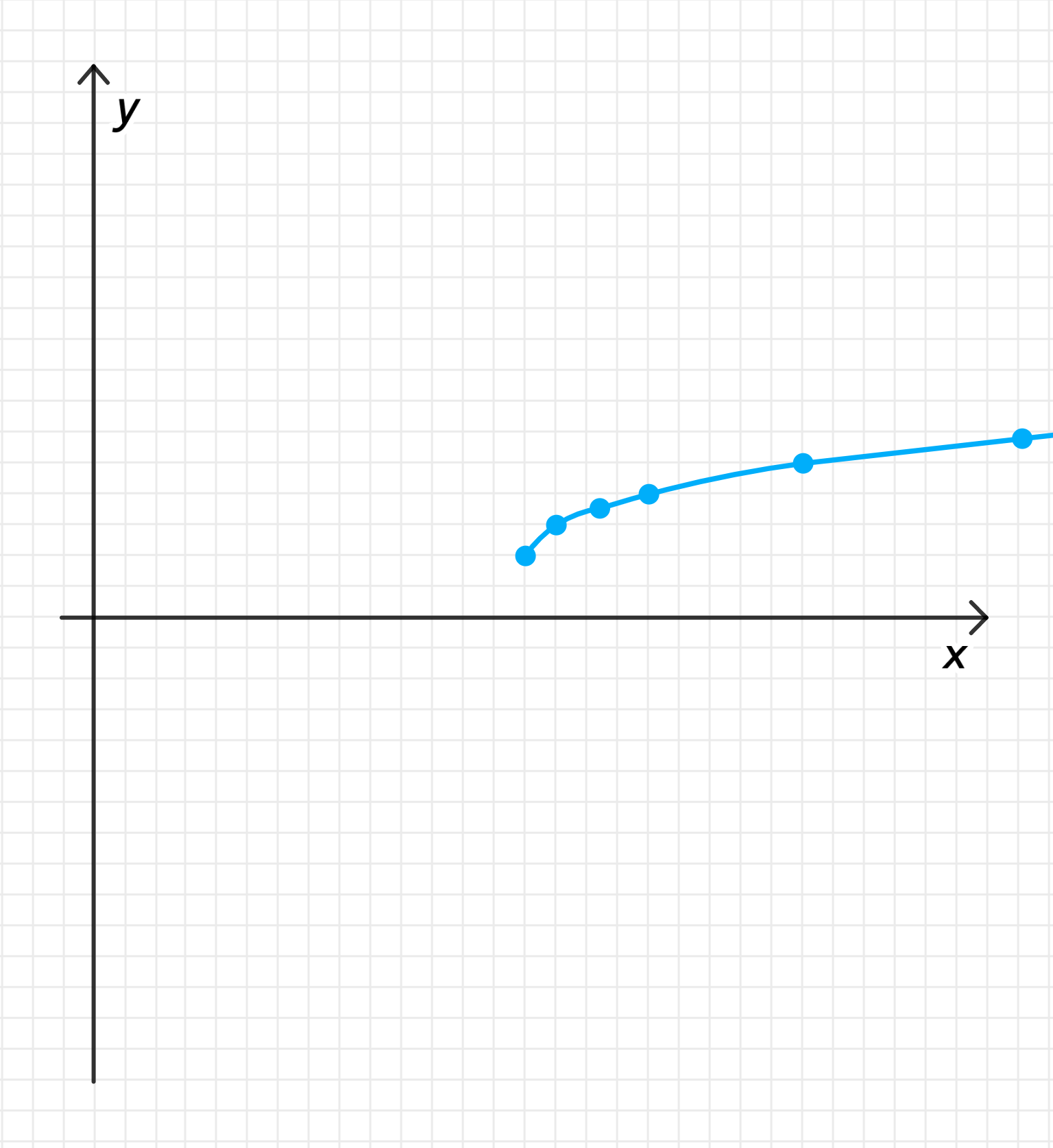Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 10.22 Профильный Уровень Мордкович — Подробные Ответы
у = x² — 4x + 18:
а) на R;
б) на [2; );
в) на (; 0];
г) на [; 3).
У квадратичной функции обратная функция может существовать только на промежутках, содержащих одну ветвь параболы;
Дана функция:
— ветви направлены вверх;
а) На множестве обратной функции не существует;
Ответ: нет.
б) На промежутке :
Множество значений функции:
Функция, обратная данной:
| 14 | 18 | 23 | |
|---|---|---|---|
| 2 | 4 | 5 |
График обратной функции:
Ответ:
в) На промежутке :
Множество значений функции:
Функция, обратная данной:
| 18 | 23 | 30 | |
|---|---|---|---|
| 0 | -1 | -2 |
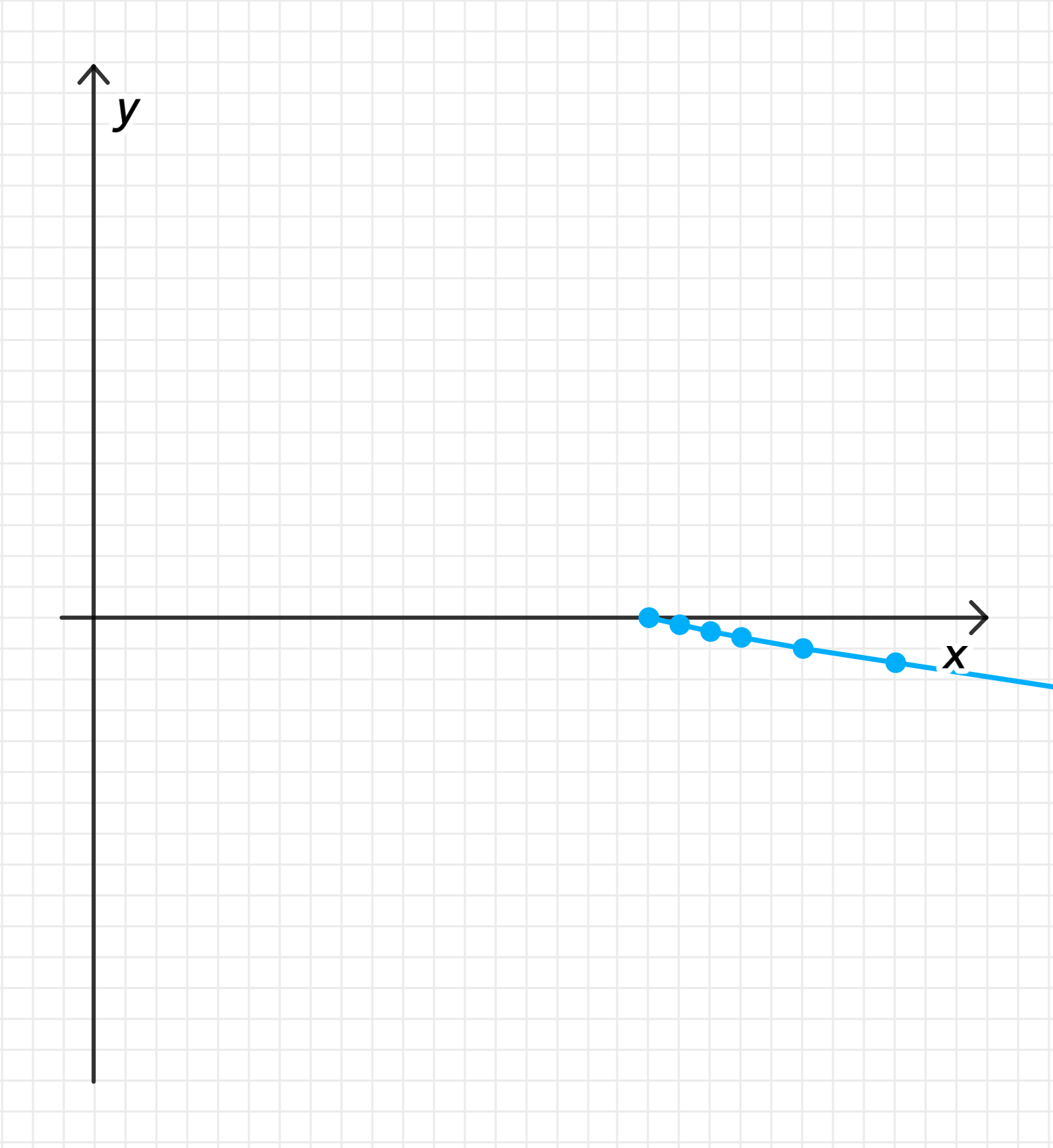
График обратной функции:
Ответ:
г) На промежутке обратной функции не существует;
Ответ: нет.
Квадратичная функция:
Мы преобразуем её в стандартный вид, чтобы лучше понять её структуру. Для этого выделим полный квадрат:
Таким образом, функция принимает вид:
Теперь определим ключевые параметры этой функции.
1. Вершина параболы:
Для квадратичной функции вида , вершина параболы находится в точке . В нашем случае:
Таким образом, вершина параболы находится в точке .
2. Направление ветвей:
Так как коэффициент перед квадратом (положительный), то парабола открывается вверх. То есть, для функция будет стремиться к бесконечности.
3. Область определения:
Область определения функции — вся действительная прямая , так как это квадратичная функция, которая определена для всех значений .
4. Область значений функции:
Парабола открывается вверх, а её вершина имеет значение . Следовательно, функция достигает минимального значения в вершине, и на всех значениях функция будет возрастать. Таким образом, область значений функции будет:
Теперь давайте перейдем к анализу функции на различных промежутках.
1. Разбор по промежуткам:
а) На множестве обратной функции не существует
Для квадратичной функции на всей области не существует обратной функции. Это связано с тем, что функция не является взаимно однозначной: для одного и того же значения существует два значения , например, для существуют значения и , которые дают одинаковое значение . Это нарушает условие взаимной однозначности, которое необходимо для существования обратной функции.
Ответ: нет, на множестве обратной функции не существует.
б) На промежутке
Этот промежуток включает только одну ветвь параболы (ветвь, направленную вверх), и на нем функция является монотонной (возрастающей). Поэтому мы можем найти её обратную функцию на этом промежутке.
1) Множество значений функции:
Для функции на промежутке :
- Минимальное значение функции при :
- Функция будет возрастать на промежутке , и её значения будут идти от до .
Множество значений функции на этом промежутке:
2) Нахождение обратной функции:
Чтобы найти обратную функцию, выразим через :
Так как на промежутке всегда больше или равен , то обратная функция будет иметь вид:
3) Таблица значений функции и её обратной:
Рассмотрим таблицу значений для функции и её обратной.
| 14 | 18 | 23 | |
|---|---|---|---|
| 2 | 4 | 5 |
4) График обратной функции:
График функции будет частью параболы, направленной вверх, с областью определения и областью значений .
Ответ:
в) На промежутке
На этом промежутке функция также является монотонной (убывающей), и на нем можно найти обратную функцию.
1) Множество значений функции:
Для функции на промежутке :
- Минимальное значение функции при :
- Функция будет убывать на промежутке , и её значения будут идти от до .
Множество значений функции на этом промежутке:
2) Нахождение обратной функции:
Для нахождения обратной функции выразим через :
На промежутке всегда меньше или равен , поэтому обратная функция будет:
3) Таблица значений функции и её обратной:
Рассмотрим таблицу значений для функции и её обратной.
| 18 | 23 | 30 | |
|---|---|---|---|
| 0 | -1 | -2 |
4) График обратной функции:
График функции будет частью параболы, направленной вниз, с областью определения и областью значений .
Ответ:
г) На промежутке обратной функции не существует
На промежутке функция не является взаимно однозначной, так как для одного и того же значения существует два значения , что нарушает условие взаимной однозначности, необходимое для существования обратной функции.
Ответ: нет, на промежутке обратной функции не существует.
Итоговый ответ:
а) На множестве обратной функции не существует. Ответ: нет.
б) На промежутке обратная функция существует. Ответ: .
в) На промежутке обратная функция существует. Ответ: .
г) На промежутке обратной функции не существует. Ответ: нет.