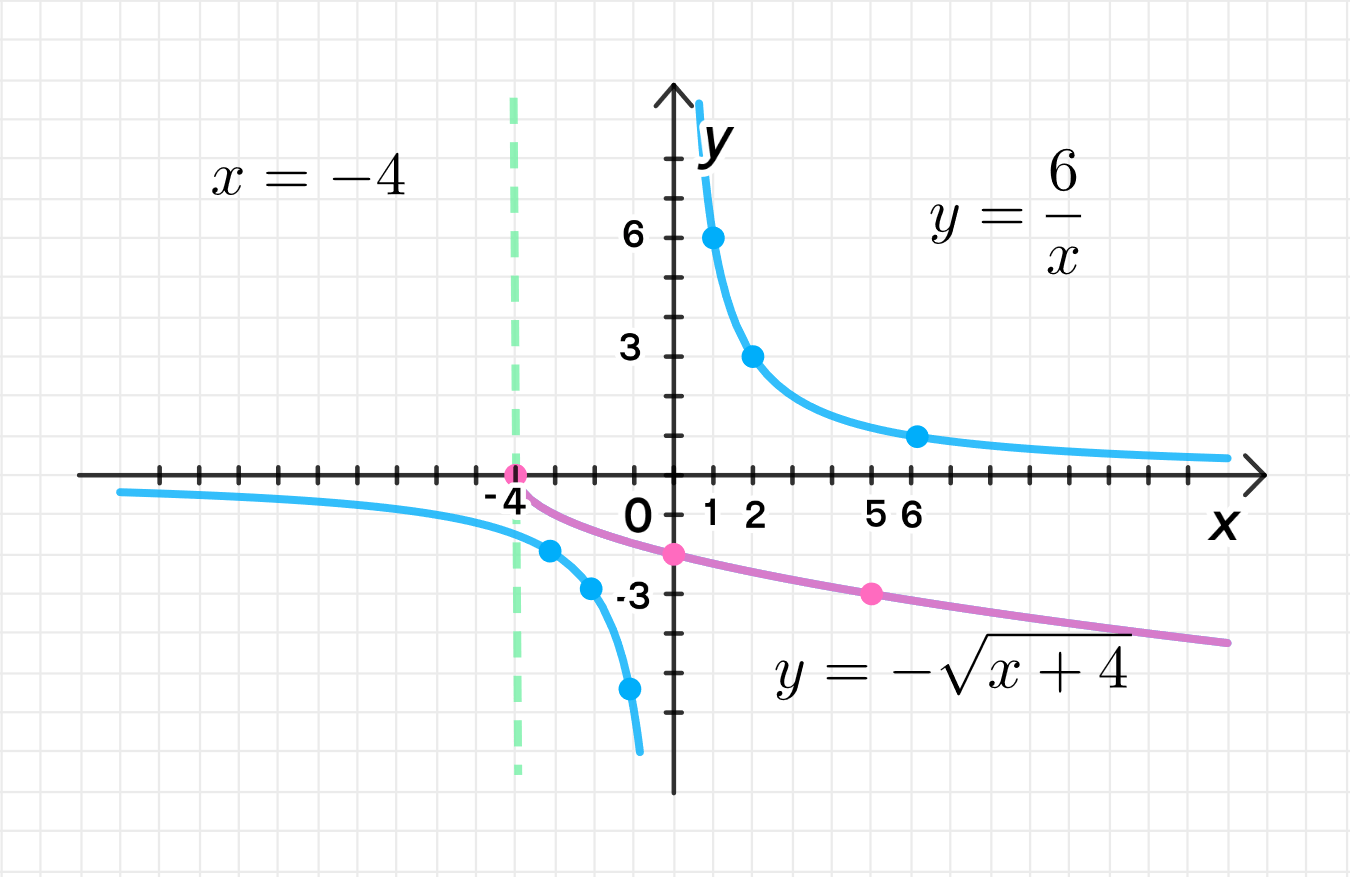ГДЗ Мордкович 10 Класс Профильный Уровень по Алгебре Задачник 📕 — Все Части

Алгебра Профильный Уровень

10 класс задачник профильный уровень Мордкович

10 класс

Тип

ГДЗ, Решебник.

Автор

А.Г. Мордкович, П. В. Семенов.

Год

2015-2020.

Издательство

Мнемозина.

Описание

Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.

ГДЗ по Алгебре 10 Класс Номер 108 Повторение Профильный Уровень Мордкович — Подробные Ответы

Задача

а) $(x y - 6) (\sqrt{x + 4} + y) = 0$

б) $(\sqrt{x^{2}} - y) (x^{2} - 4 x + y) = 0$

в) $(2 x + y) (x^{3} - y - 1) = 0$

г) $(y - x) (x + 4) = 0$

Краткий ответ:

а) $(x y - 6) (\sqrt{x + 4} + y) = 0$

Выражение имеет смысл при:

$x + 4 \geq 0, отсюда x \geq - 4;$

Первая функция:

$x y - 6 = 0;$ $x y = 6;$ $y = \frac{6}{x} — уравнение гиперболы:$ $x_{0} = 0 и y_{0} = 0;$

$x$	$- 4$	$- 2$	$- 1$	$1$	$3$	$6$
$y$	$- 1.5$	$- 3$	$- 6$	$6$	$2$	$1$

Вторая функция:

$\sqrt{x + 4} + y = 0;$ $y = - \sqrt{x + 4} — уравнение ветви параболы:$ $x_{0} = - 4 и y_{0} = 0;$

$x$	$- 3$	$0$	$5$
$y$	$- 1$	$- 2$	$- 3$

График уравнения:

б) $(\sqrt{x^{2}} - y) (x^{2} - 4 x + y) = 0$

Первая функция:

$\sqrt{x^{2}} - y = 0;$ $∣ x ∣ - y = 0;$ $y = ∣ x ∣ — график модуля:$ $x_{0} = 0 и y_{0} = 0;$

$x$	$- 2$	$2$
$y$	$2$	$2$

Вторая функция:

$x^{2} - 4 x + y = 0;$ $y = 4 x - x^{2} — уравнение параболы:$ $x_{0} = - \frac{4}{- 1 \cdot 2} = 2 и y_{0} = 4;$

$x$	$- 1$	$0$	$1$	$3$	$4$	$5$
$y$	$- 5$	$0$	$3$	$3$	$0$	$- 5$

График уравнения:

в) $(2 x + y) (x^{3} - y - 1) = 0$

Первая функция:

$2 x + y = 0;$ $y = - 2 x — уравнение прямой:$

$x$	$0$	$1$
$y$	$0$	$- 2$

Вторая функция:

$x^{3} - y - 1 = 0;$ $y = x^{3} - 1 — уравнение кубической параболы:$ $x_{0} = 0 и y_{0} = - 1;$

$x$	$- 2$	$- 1$	$1$	$2$
$y$	$- 9$	$- 2$	$0$	$7$

График уравнения:

г) $(y - x) (x + 4) = 0$

Первая функция:

$y - x = 0;$ $y = x — уравнение прямой:$

$x$	$1$	$2$
$y$	$1$	$2$

Вторая функция:

$x + 4 = 0;$ $x = - 4 — уравнение прямой;$

График уравнения:

Подробный ответ:

а) $(x y - 6) (\sqrt{x + 4} + y) = 0$

Для данного уравнения произведение двух выражений равно нулю. Это означает, что одно из выражений должно быть равно нулю. Мы рассматриваем два случая:

$(x y - 6) = 0 или (\sqrt{x + 4} + y) = 0.$

1) Первое выражение: $x y - 6 = 0$

Перепишем это уравнение:

$x y = 6$

Решим его относительно $y$ :

$y = \frac{6}{x} .$

Это уравнение гиперболы, где центр гиперболы находится в точке $(0, 0)$ . Теперь построим таблицу значений для разных $x$ :

$x$	$- 4$	$- 2$	$- 1$	$1$	$3$	$6$
$y$	$- 1.5$	$- 3$	$- 6$	$6$	$2$	$1$

Примечание: Мы видим, что гипербола пересекает оси $x$ и $y$ , но не в центре. Эти значения служат точками на графике гиперболы.

2) Второе выражение: $\sqrt{x + 4} + y = 0$

Перепишем уравнение:

$y = - \sqrt{x + 4} .$

Это уравнение представляет собой ветвь параболы, которая начинается в точке $(x_{0}, y_{0}) = (- 4, 0)$ , так как корень из $x + 4$ существует только при $x \geq - 4$ .

Теперь найдем значения $y$ для различных значений $x$ :

$x$	$- 3$	$0$	$5$
$y$	$- 1$	$- 2$	$- 3$

Примечание: График данной функции — это парабола, которая начинает свою ветвь в точке $(- 4, 0)$ .

3) График уравнения:

б) $(\sqrt{x^{2}} - y) (x^{2} - 4 x + y) = 0$

Для данного уравнения также произведение двух выражений равно нулю, следовательно, одно из выражений должно быть равно нулю.

$(\sqrt{x^{2}} - y) = 0 или (x^{2} - 4 x + y) = 0.$

1) Первое выражение: $\sqrt{x^{2}} - y = 0$

Перепишем уравнение:

$∣ x ∣ - y = 0 \Rightarrow y = ∣ x ∣ .$

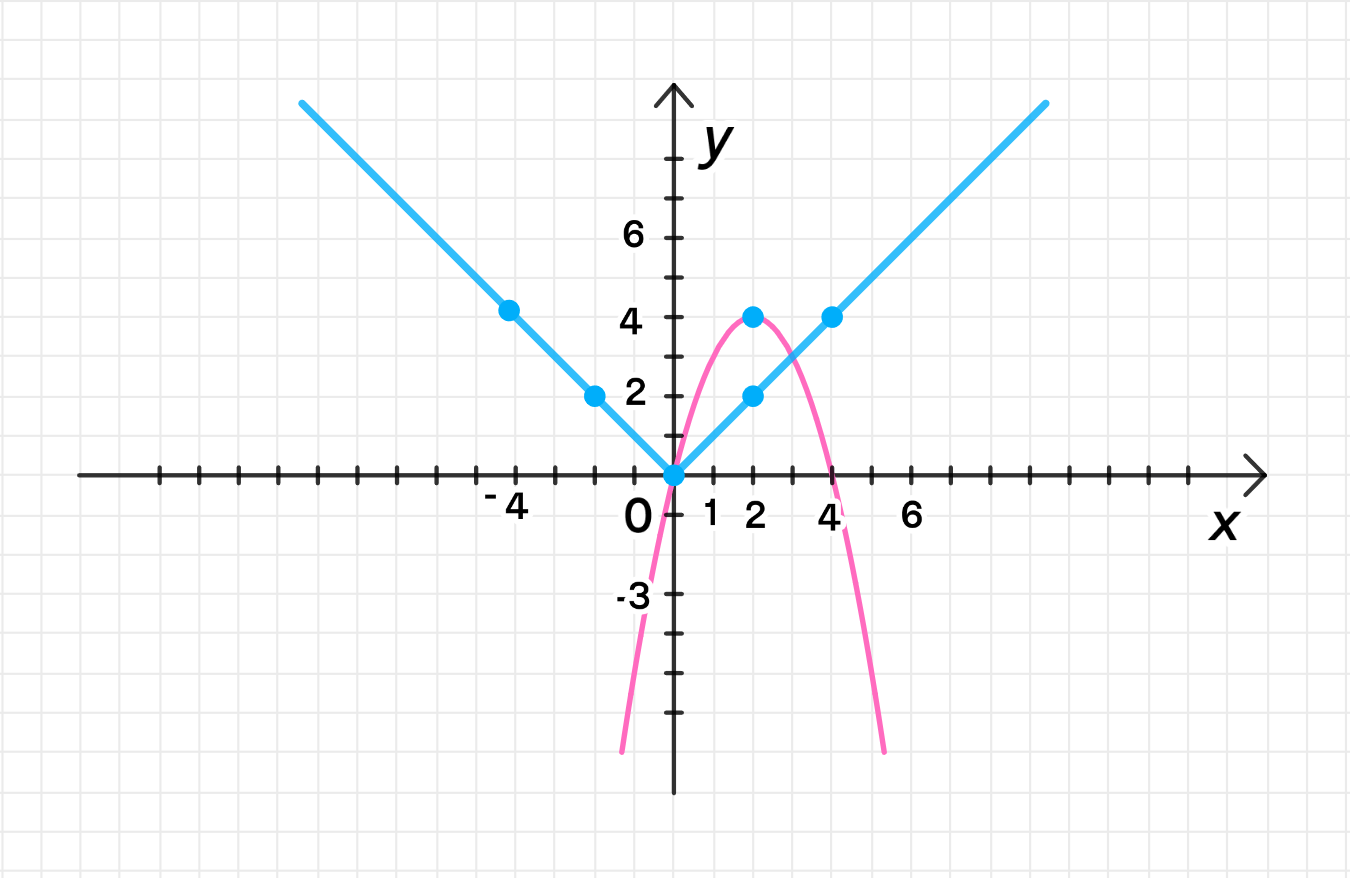
Это уравнение модуля, и оно представляет собой график, состоящий из двух прямых: одна с угловым коэффициентом $+ 1$ (для положительных значений $x$ ), а другая — с угловым коэффициентом $- 1$ (для отрицательных значений $x$ ).

Для нескольких значений $x$ получаем:

$x$	$- 2$	$2$
$y$	$2$	$2$

Примечание: Это график двух прямых, пересекающихся в начале координат.

2) Второе выражение: $x^{2} - 4 x + y = 0$

Перепишем уравнение:

$y = 4 x - x^{2} .$

Это уравнение параболы, которая имеет вершину в точке $(x_{0}, y_{0}) = (2, 4)$ . Парабола открывается вниз.

Для нескольких значений $x$ получаем:

$x$	$- 1$	$0$	$1$	$3$	$4$	$5$
$y$	$- 5$	$0$	$3$	$3$	$0$	$- 5$

Примечание: Это парабола, которая имеет вершину в точке $(2, 4)$ .

3) График уравнения:

в) $(2 x + y) (x^{3} - y - 1) = 0$

Произведение двух выражений снова равно нулю, поэтому рассматриваем два случая.

$(2 x + y) = 0 или (x^{3} - y - 1) = 0.$

1) Первое выражение: $2 x + y = 0$

Перепишем уравнение:

$y = - 2 x .$

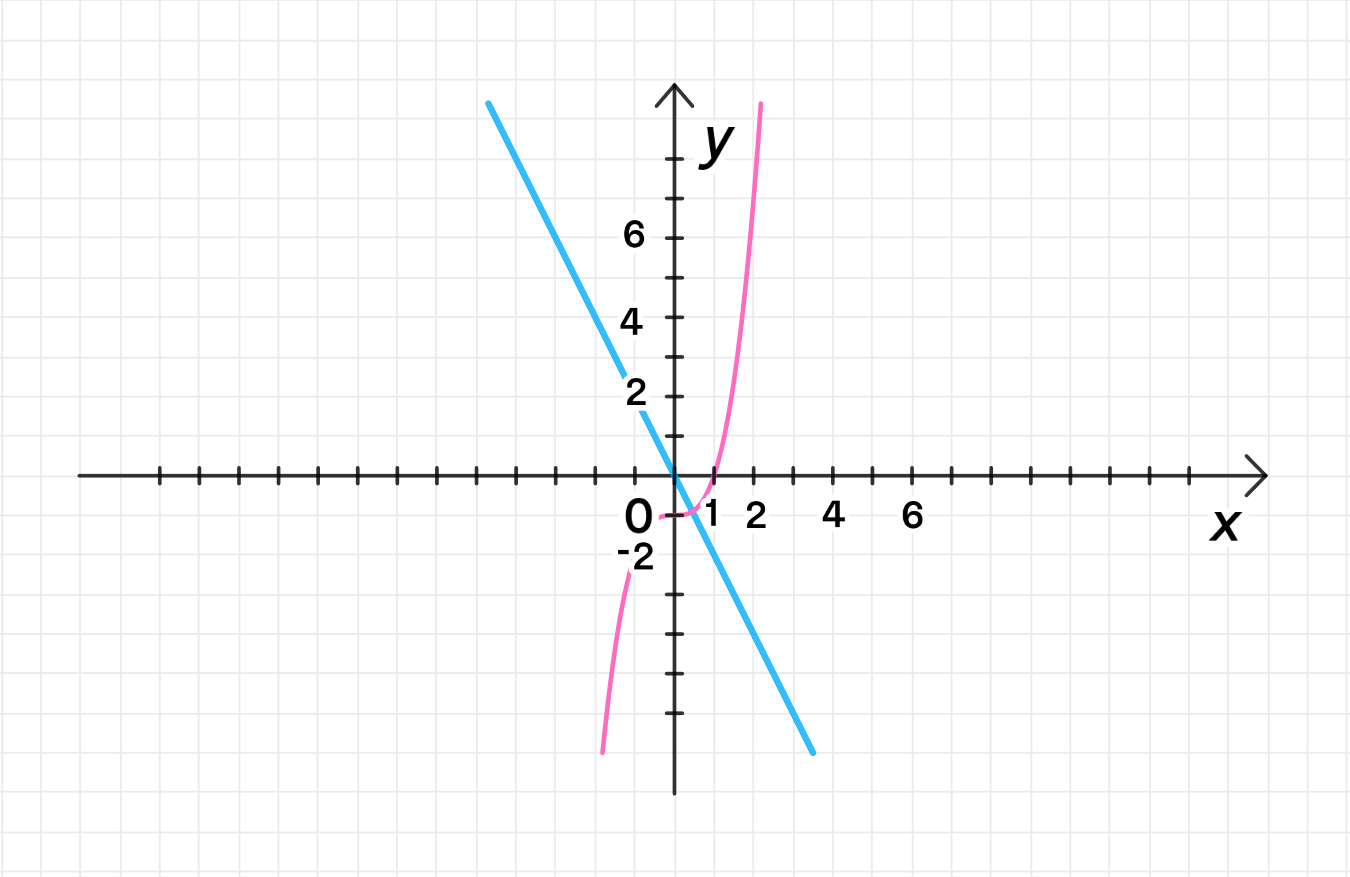
Это уравнение прямой с угловым коэффициентом $- 2$ . График этой прямой пересекает начало координат.

Для нескольких значений $x$ получаем:

$x$	$0$	$1$
$y$	$0$	$- 2$

Примечание: Это прямая линия с угловым коэффициентом $- 2$ , которая проходит через начало координат.

2) Второе выражение: $x^{3} - y - 1 = 0$

Перепишем уравнение:

$y = x^{3} - 1.$

Это уравнение кубической параболы, которая имеет точку пересечения с осью $y$ в точке $(0, - 1)$ .

Для нескольких значений $x$ получаем:

$x$	$- 2$	$- 1$	$1$	$2$
$y$	$- 9$	$- 2$	$0$	$7$

Примечание: Это кубическая парабола, которая начинает от точки $(0, - 1)$ .

3) График уравнения:

г) $(y - x) (x + 4) = 0$

Произведение двух выражений равно нулю, так что одно из выражений должно быть равно нулю.

$(y - x) = 0 или (x + 4) = 0.$

1) Первое выражение: $y - x = 0$

Перепишем уравнение:

$y = x .$

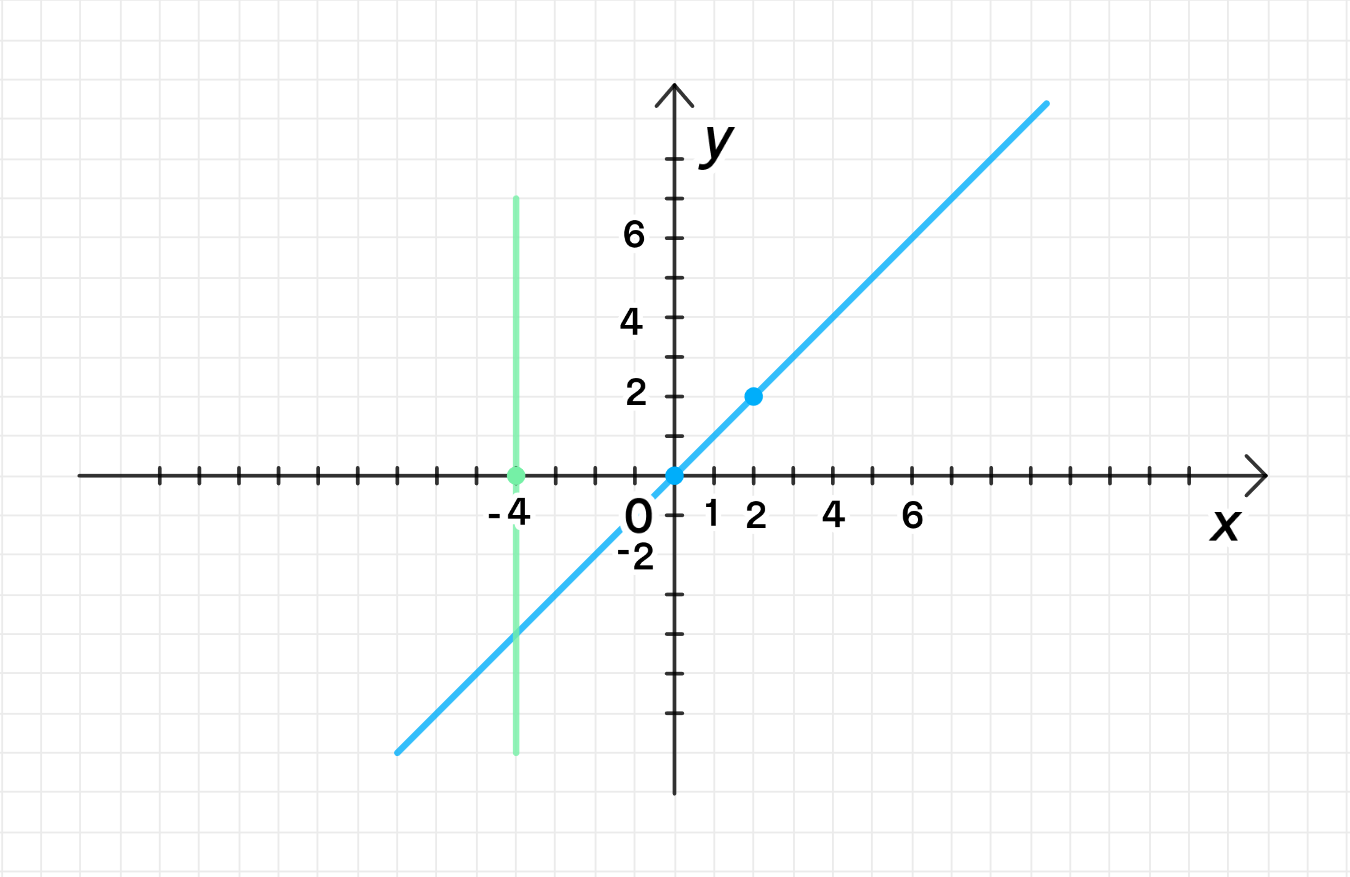
Это уравнение прямой с угловым коэффициентом $1$ , которая проходит через начало координат.

Для нескольких значений $x$ получаем:

$x$	$1$	$2$
$y$	$1$	$2$

Примечание: Это прямая линия с угловым коэффициентом $1$ , которая проходит через начало координат.

2) Второе выражение: $x + 4 = 0$

Перепишем уравнение:

$x = - 4.$

Это уравнение вертикальной прямой, которая проходит через точку $x = - 4$ .

3) График уравнения:

Оцени решение