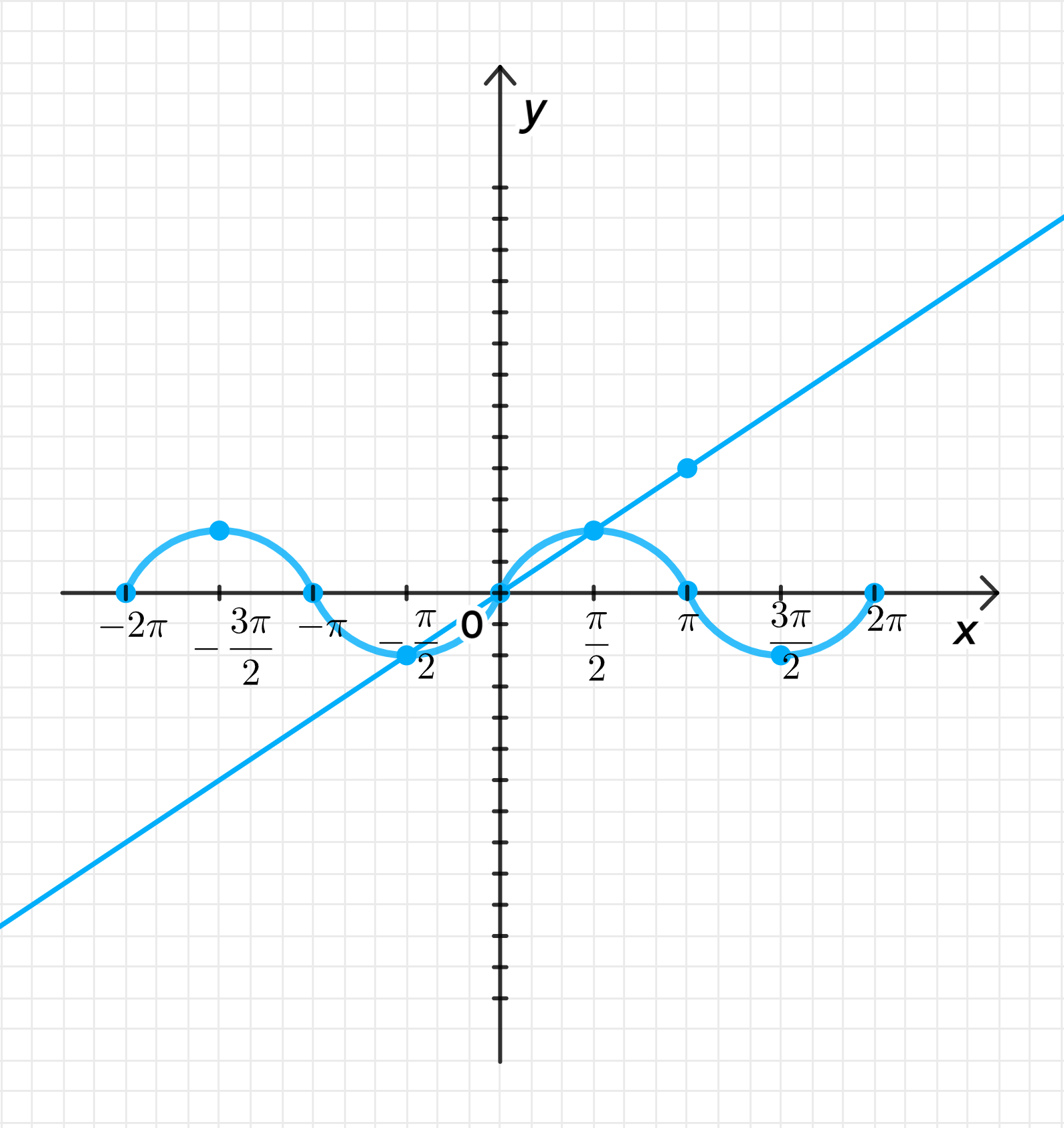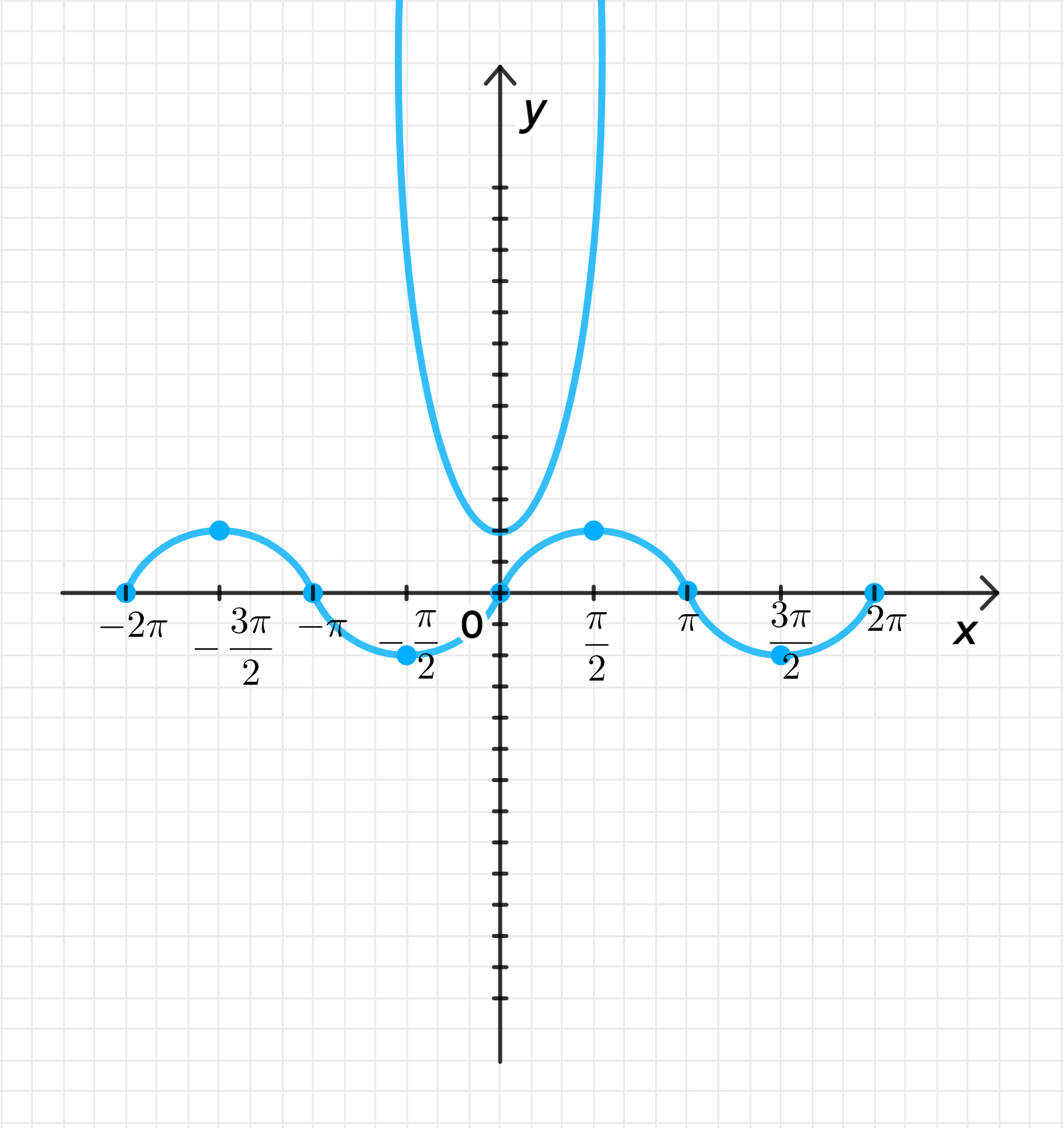Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 16.20 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
а) ;
— уравнение синусоиды;
— уравнение прямой:
| 0 | ||
|---|---|---|
| 0 | 2 |
Графики функций:
Ответ: .
б) ;
Преобразуем уравнение:
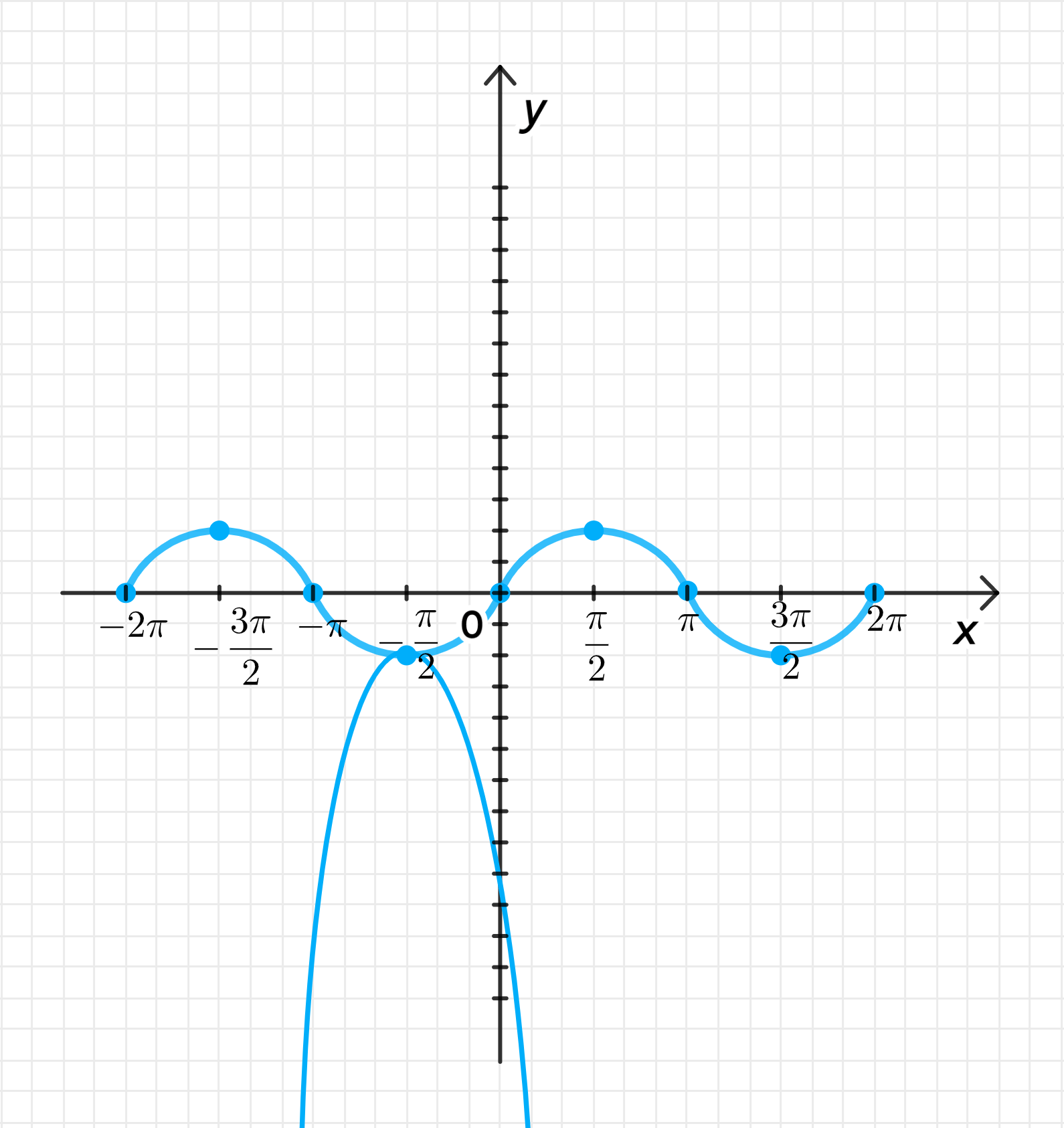
— уравнение синусоиды;
— уравнение параболы:
| 0 | |||
|---|---|---|---|
| ≈ -3,5 | -1 | ≈ -3,5 |
Графики функций:
Ответ: .
в) ;
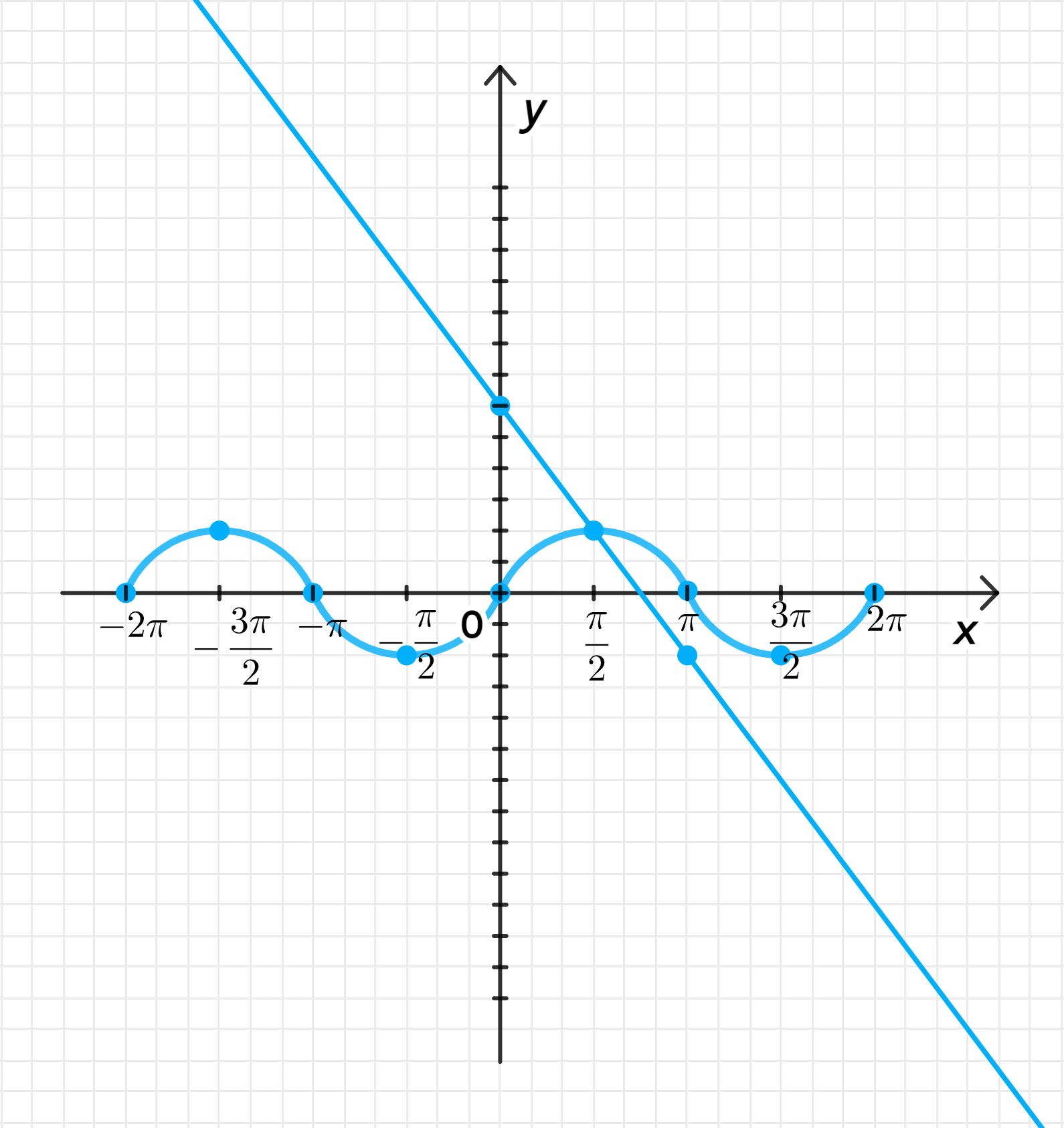
— уравнение синусоиды;
— уравнение прямой:
| 0 | ||
|---|---|---|
| 3 | -1 |
Графики функций:
Ответ: .
г) ;
— уравнение синусоиды;
— уравнение параболы:
| -1 | 0 | 1 | |
|---|---|---|---|
| 2 | 1 | 2 |
Графики функций:
Ответ: нет корней.
а)
1. Уравнение синусоиды и прямой:
- — уравнение синусоиды. График функции представляет собой волну, которая колеблется от до с периодом . То есть для каждого функция принимает значения в пределах от до .
- — уравнение прямой, где угловой коэффициент равен . Это линейная функция, которая растет с угловым коэффициентом , то есть за каждый шаг на 1, увеличивается на .
2. Вычисление значений для построения графиков:
Для более точного построения графиков подставим несколько значений в обе функции и посмотрим, как они себя ведут.
- Для :
- При , .
- При , .
- При , .
- При , .
- Для :
- При , .
- При , .
- При , .
- При , .
| 0 | |||
|---|---|---|---|
| 0 | 1 | 0 | |
| 0 | 1 | 2 |
3. Построение графиков:
- График будет волнообразным, колеблющимся от до .
- График будет прямой, растущей с угловым коэффициентом .
4. Пересечение графиков:
Найдем точку пересечения графиков, решив уравнение:
Решение этого уравнения может быть найдено как графически, так и численно. Графически видно, что функции пересекаются в трех точках: , и . Проверим, что они действительно равны в этих точках.
- При , обе функции дают .
- При , обе функции также дают .
Ответ: .
б)
1. Преобразование уравнения:
Для удобства перепишем уравнение:
2. Уравнение синусоиды и параболы:
- — уравнение синусоиды, которая колеблется между и .
- — уравнение параболы, которая сдвинута по оси вниз на 1 единицу и направлена вниз, так как перед квадратичным членом стоит минус.
3. Вычисление значений для построения графиков:
Для построения графиков подставим несколько значений :
- Для :
- При , .
- При , .
- При , .
- Для :
- При , .
- При , .
- При , .
| 0 | |||
|---|---|---|---|
| 0 | -1 | 0 | |
| ≈ -3.46 | -1 | ≈ -2.47 |
4. Построение графиков:
- График будет волнообразным.
- График — парабола, направленная вниз и сдвинутая вниз на 1.
5. Пересечение графиков:
Решаем уравнение:
Графически видно, что функции пересекаются только в одной точке: , что подтверждается расчетами.
Ответ: .
в)
1. Уравнение синусоиды и прямой:
- — уравнение синусоиды.
- — уравнение прямой, с угловым коэффициентом , что означает, что прямая будет иметь наклон вниз.
2. Вычисление значений для построения графиков:
Подставим несколько значений для построения графиков:
- Для :
- При , .
- При , .
- Для :
- При , .
- При , .
| 0 | ||
|---|---|---|
| 0 | 0 | |
| 3 | -1 |
3. Построение графиков:
- График будет волнообразным.
- График будет прямой с угловым коэффициентом .
4. Пересечение графиков:
Решаем уравнение:
Очевидно, что функции пересекаются в точке , что подтверждается графически.
Ответ: .
г)
1. Уравнение синусоиды и параболы:
- — уравнение синусоиды.
- — уравнение параболы, направленной вверх, с вершиной в точке .
2. Вычисление значений для построения графиков:
Подставим несколько значений для построения графиков:
- Для :
- При , .
- При , .
- Для :
- При , .
- При , .
- При , .
| -1 | 0 | 1 | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 2 | 1 | 2 |
3. Построение графиков:
- График — волнообразная функция.
- График — парабола, направленная вверх.
4. Пересечение графиков:
Решаем уравнение:
Графически видно, что функции не пересекаются, так как синусоида колеблется между и , а парабола всегда лежит выше этой области.
Ответ: нет корней.