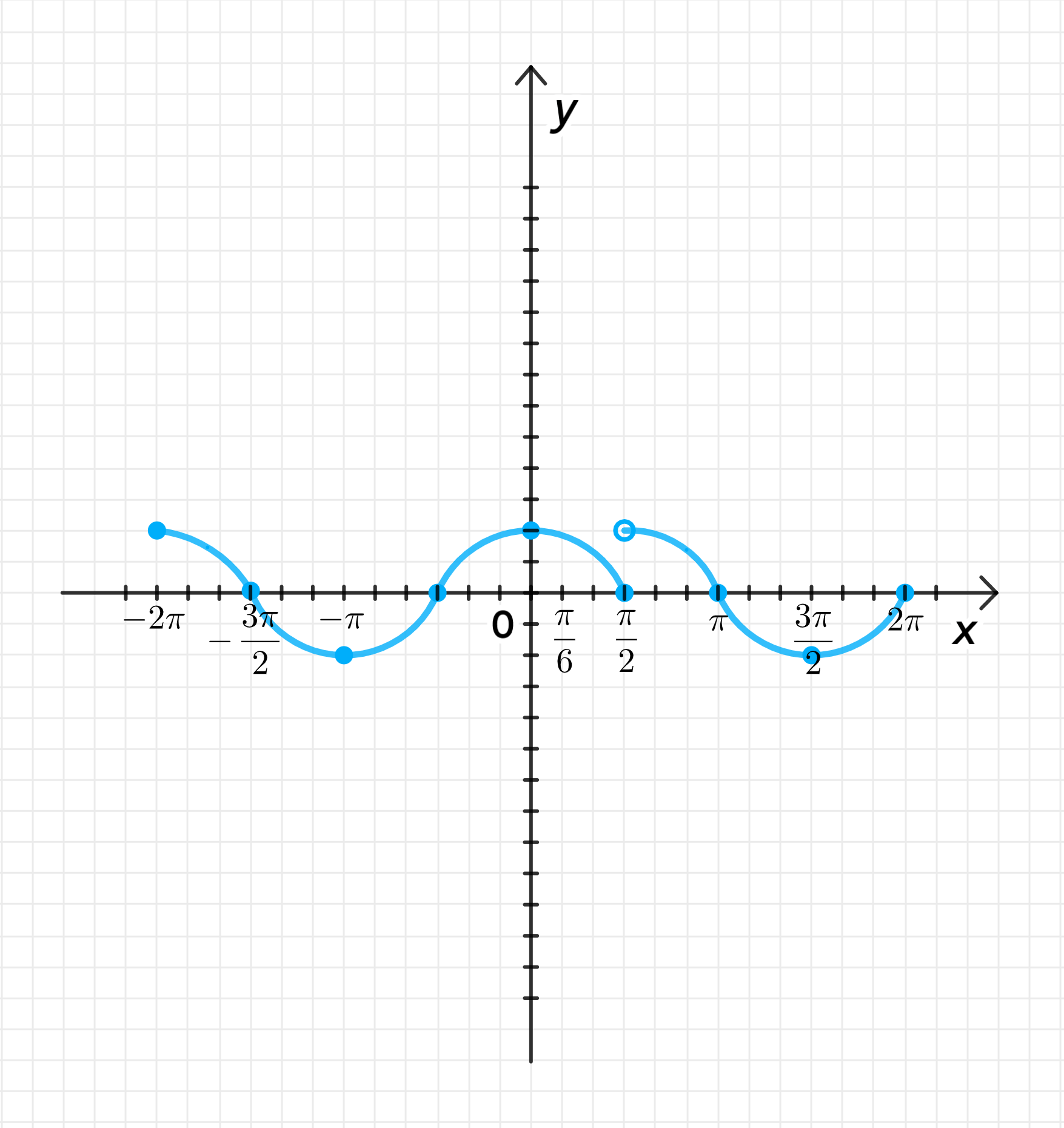Задача
а) y = { cos x , если x ≤ π 2 ; sin x , если x > π 2 y = \begin{cases} \cos x, & \text{если } x \leq \frac{\pi}{2}; \\ \sin x, & \text{если } x > \frac{\pi}{2} \end{cases}
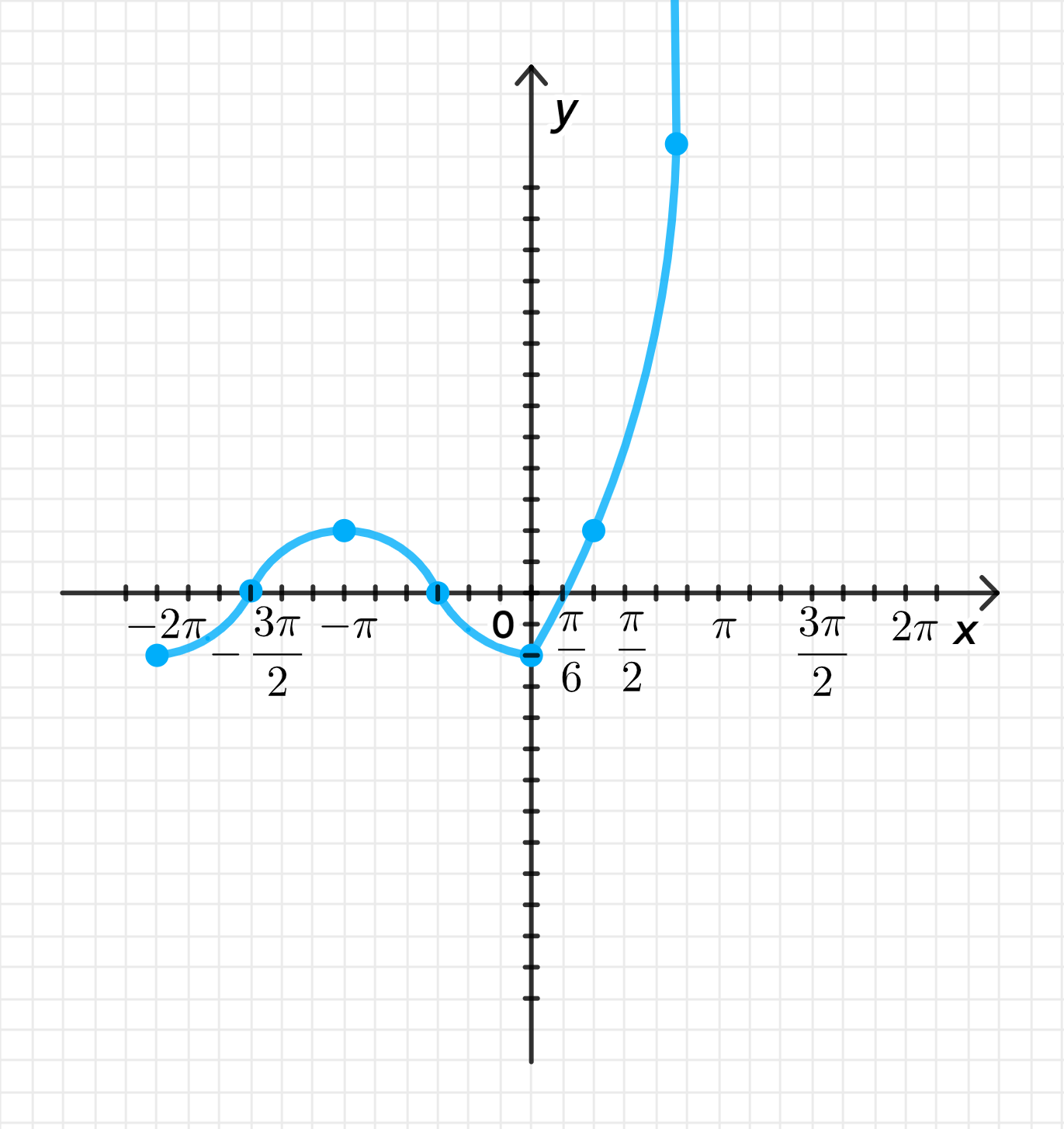
б) y = { − cos x , если x < 0 ; 2 x 2 − 1 , если x ≥ 0
Краткий ответ:
В данной задаче n n
а) y = { cos x , если x ≤ π 2 ; sin x , если x > π 2 y = \begin{cases} \cos x, & \text{если } x \leq \frac{\pi}{2}; \\ \sin x, & \text{если } x > \frac{\pi}{2} \end{cases}
y = cos x y = \cos x y ( π 2 ) = cos π 2 = 0 ; y\left(\frac{\pi}{2}\right) = \cos \frac{\pi}{2} = 0;
y = sin x y = \sin x y ( π 2 ) = sin π 2 = 1 ; y\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1;
Графики функции:
Свойства функции:
Область определения: D ( f ) = ( − ∞ ; + ∞ ) ; D(f) = (-\infty; +\infty); Множество значений: E ( f ) = [ − 1 ; 1 ] ; E(f) = [-1; 1]; Возрастает на [ − π − 2 π n ; − 2 π n ] ∪ [ 3 π 2 + 2 π n ; 5 π 2 + 2 π n ] ; [-\pi — 2\pi n; -2\pi n] \cup \left[\frac{3\pi}{2} + 2\pi n; \frac{5\pi}{2} + 2\pi n\right]; Убывает на [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; π 2 ] ∪ [ π 2 + 2 π n ; 3 π 2 + 2 π n ] ; [-2\pi — 2\pi n; -\pi — 2\pi n] \cup \left[0; \frac{\pi}{2}\right] \cup \left[\frac{\pi}{2} + 2\pi n; \frac{3\pi}{2} + 2\pi n\right]; f ( x ) > 0 f(x) > 0 ( − π 2 − 2 π n ; π 2 − 2 π n ) ∪ ( π 2 ; π ) ∪ ( 2 π + 2 π n ; 3 π + 2 π n ) ; \left(-\frac{\pi}{2} — 2\pi n; \frac{\pi}{2} — 2\pi n\right) \cup \left(\frac{\pi}{2}; \pi\right) \cup (2\pi + 2\pi n; 3\pi + 2\pi n); f ( x ) < 0 f(x) < 0 ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( π + 2 π n ; 2 π + 2 π n ) ; \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup (\pi + 2\pi n; 2\pi + 2\pi n); Функция ни четная, ни нечетная; Функция не является периодической б) y = { − cos x , если x < 0 ; 2 x 2 − 1 , если x ≥ 0 y = \begin{cases} -\cos x, & \text{если } x < 0; \\ 2x^2 — 1, & \text{если } x \geq 0 \end{cases}
y = − cos x y = -\cos x y ( 0 ) = − cos 0 = − 1 ; y(0) = -\cos 0 = -1;
y = 2 x 2 − 1 y = 2x^2 — 1 x 0 = 0 , y 0 = − 1 ; x_0 = 0, \quad y_0 = -1;
Графики функции:
Свойства функции:
Область определения: D ( f ) = ( − ∞ ; + ∞ ) ; D(f) = (-\infty; +\infty); Множество значений: E ( f ) = [ − 1 ; + ∞ ) ; E(f) = [-1; +\infty); Возрастает на [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; + ∞ ) ; [-2\pi — 2\pi n; -\pi — 2\pi n] \cup [0; +\infty); Убывает на [ − π − 2 π n ; − 2 π n ] ; [-\pi — 2\pi n; -2\pi n]; f ( x ) > 0 f(x) > 0 ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( 1 2 ; + ∞ ) ; \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup \left(\frac{1}{\sqrt{2}}; +\infty\right); f ( x ) < 0 f(x) < 0 ( − 5 π 2 − 2 π n ; − 3 π 2 − 2 π n ) ∪ ( − π 2 ; 1 2 ) ; \left(-\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n\right) \cup \left(-\frac{\pi}{2}; \frac{1}{\sqrt{2}}\right); Функция ни четная, ни нечетная; Функция не является периодической Подробный ответ:
а) Функция:
y = { cos x , если x ≤ π 2 ; sin x , если x > π 2 . y = \begin{cases} \cos x, & \text{если } x \leq \frac{\pi}{2}; \\ \sin x, & \text{если } x > \frac{\pi}{2}. \end{cases}
1. Обработка каждого из случаев функции
1) y = cos x y = \cos x — уравнение синусоиды для x ≤ π 2 x \leq \frac{\pi}{2}
y ( π 2 ) = cos π 2 = 0. y\left(\frac{\pi}{2}\right) = \cos \frac{\pi}{2} = 0.
Здесь мы видим, что при x = π 2 x = \frac{\pi}{2}
2) y = sin x y = \sin x — уравнение синусоиды для x > π 2 x > \frac{\pi}{2}
y ( π 2 ) = sin π 2 = 1. y\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1.
При x = π 2 x = \frac{\pi}{2}
2. Графики функции
3. Свойства функции
Область определения D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) x x cos x \cos x sin x \sin x Множество значений E ( f ) = [ − 1 ; 1 ] E(f) = [-1; 1] cos x \cos x sin x \sin x Возрастает на [ − π − 2 π n ; − 2 π n ] ∪ [ 3 π 2 + 2 π n ; 5 π 2 + 2 π n ] [-\pi — 2\pi n; -2\pi n] \cup \left[\frac{3\pi}{2} + 2\pi n; \frac{5\pi}{2} + 2\pi n\right] x x Убывает на [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; π 2 ] ∪ [ π 2 + 2 π n ; 3 π 2 + 2 π n ] [-2\pi — 2\pi n; -\pi — 2\pi n] \cup \left[0; \frac{\pi}{2}\right] \cup \left[\frac{\pi}{2} + 2\pi n; \frac{3\pi}{2} + 2\pi n\right] y = cos x y = \cos x Функция f ( x ) > 0 f(x) > 0 на ( − π 2 − 2 π n ; π 2 − 2 π n ) ∪ ( π 2 ; π ) ∪ ( 2 π + 2 π n ; 3 π + 2 π n ) \left(-\frac{\pi}{2} — 2\pi n; \frac{\pi}{2} — 2\pi n\right) \cup \left(\frac{\pi}{2}; \pi\right) \cup (2\pi + 2\pi n; 3\pi + 2\pi n) Функция f ( x ) < 0 f(x) < 0 на ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( π + 2 π n ; 2 π + 2 π n ) \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup (\pi + 2\pi n; 2\pi + 2\pi n) Четность : функция ни четная, ни нечетная, так как она меняет свою форму на x = π 2 x = \frac{\pi}{2} Периодичность : функция не является периодической, так как она не повторяется на всех значениях x x б) Функция:
y = { − cos x , если x < 0 ; 2 x 2 − 1 , если x ≥ 0. y = \begin{cases} -\cos x, & \text{если } x < 0; \\ 2x^2 — 1, & \text{если } x \geq 0. \end{cases}
1. Обработка каждого из случаев функции
1) y = − cos x y = -\cos x — уравнение синусоиды для x < 0 x < 0
y ( 0 ) = − cos 0 = − 1. y(0) = -\cos 0 = -1.
Когда x x
2) y = 2 x 2 − 1 y = 2x^2 — 1 — уравнение параболы для x ≥ 0 x \geq 0
x 0 = 0 , y 0 = − 1. x_0 = 0, \quad y_0 = -1.
Для x = 0 x = 0 y = − 1 y = -1
2. Графики функции
3. Свойства функции
Область определения D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) x x − cos x -\cos x 2 x 2 − 1 2x^2 — 1 Множество значений E ( f ) = [ − 1 ; + ∞ ) E(f) = [-1; +\infty) x ≥ 0 x \geq 0 Возрастает на [ − 2 π − 2 π n ; − π − 2 π n ] ∪ [ 0 ; + ∞ ) [-2\pi — 2\pi n; -\pi — 2\pi n] \cup [0; +\infty) x ≥ 0 x \geq 0 Убывает на [ − π − 2 π n ; − 2 π n ] [-\pi — 2\pi n; -2\pi n] Функция f ( x ) > 0 f(x) > 0 на ( − 3 π 2 − 2 π n ; − π 2 − 2 π n ) ∪ ( 1 2 ; + ∞ ) \left(-\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right) \cup \left(\frac{1}{\sqrt{2}}; +\infty\right) Функция f ( x ) < 0 f(x) < 0 на ( − 5 π 2 − 2 π n ; − 3 π 2 − 2 π n ) ∪ ( − π 2 ; 1 2 ) \left(-\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n\right) \cup \left(-\frac{\pi}{2}; \frac{1}{\sqrt{2}}\right) Четность : функция ни четная, ни нечетная, так как на положительной и отрицательной части прямой функция имеет разные формы.Периодичность : функция не является периодической, поскольку она включает параболическую часть, которая не повторяется.