Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 21.41 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б)
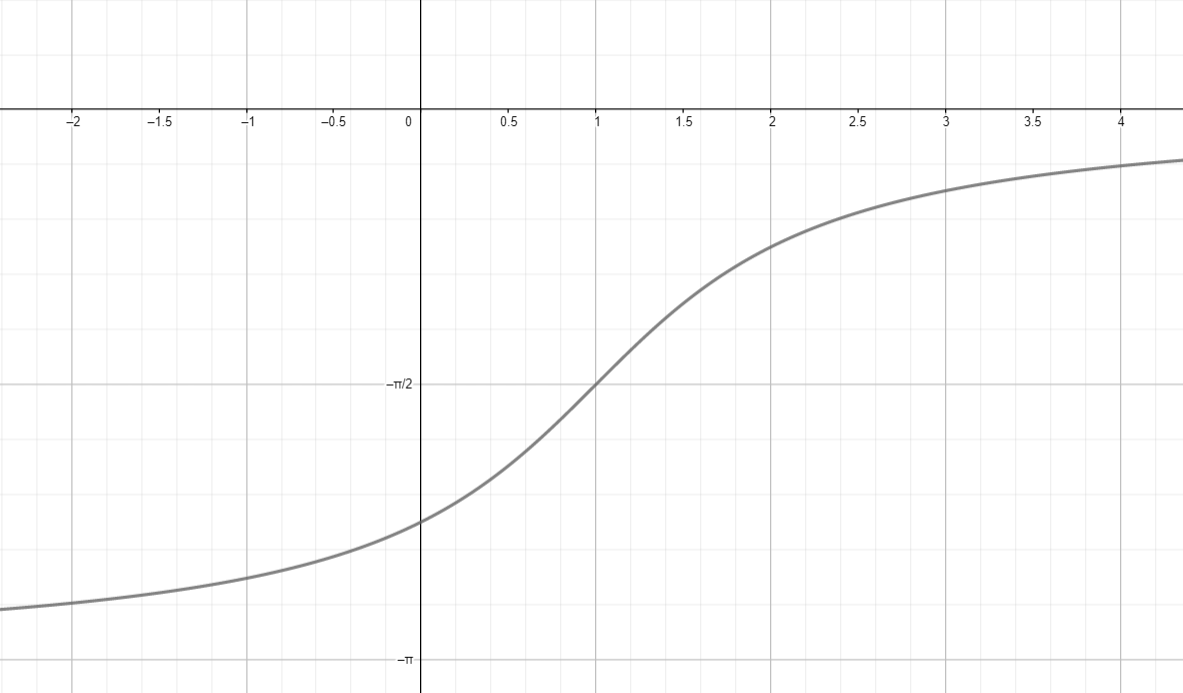
а) ;
Построим график функции ;
Переместим его на 1 единицу вправо вдоль оси абсцисс;
Переместим его на единиц вниз вдоль оси ординат:
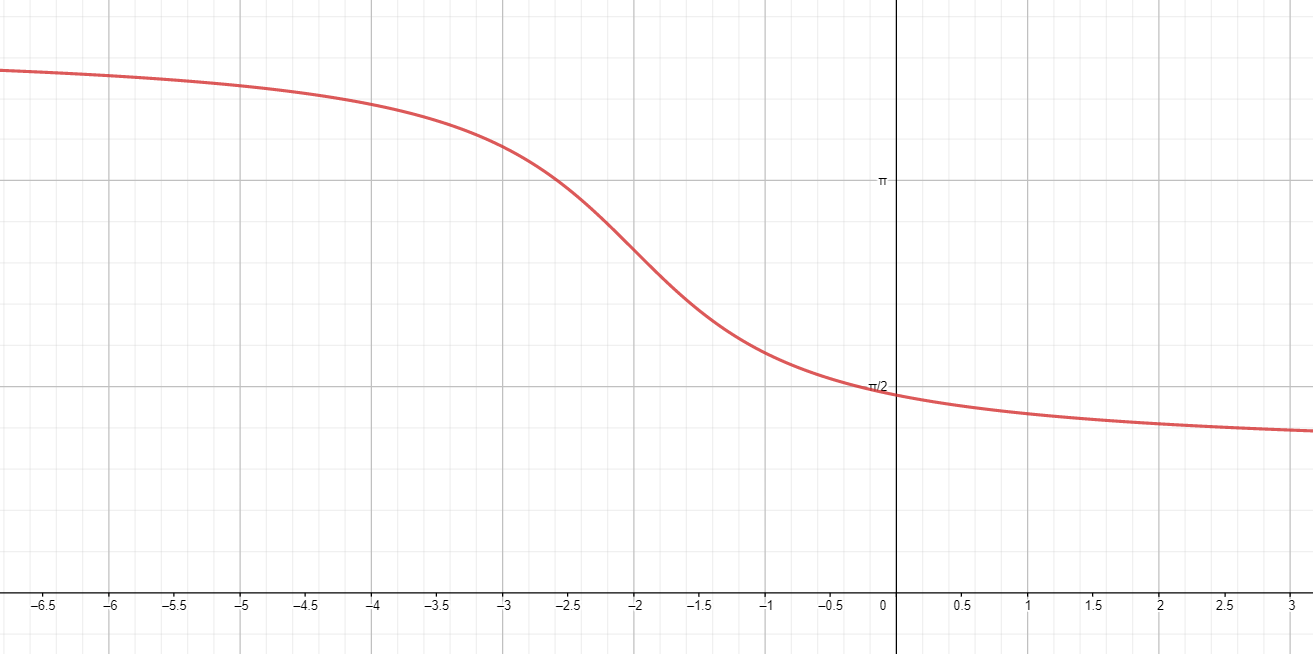
б) ;
Построим график функции ;
Переместим его на 2 единицы влево вдоль оси абсцисс;
Переместим его на единиц вверх вдоль оси ординат:
а)
Построим график функции :
- Функция (обратный арктангенс) определена на всем множестве действительных чисел .
- График функции имеет вертикальные асимптоты при , стремясь к значениям для и для .
- График выглядит как гладкая кривая, проходящая через начало координат , и асимптотически приближается к прямым и .
Переместим график на 1 единицу вправо вдоль оси абсцисс:
- Это означает замену на в функции, то есть вместо получаем:
- Сдвиг графика на 1 единицу вправо приводит к тому, что точка, где раньше график пересекал ось (в точке ), теперь будет находиться в точке .
- Это сдвиг на 1 единицу вправо вдоль оси , при этом сама форма графика остаётся неизменной.
Переместим график на единиц вниз вдоль оси ординат:
- Это означает вычитание из выражения для , то есть:
- Сдвиг графика вниз на единиц приводит к тому, что каждая точка на графике сдвигается вниз на . Например, точка пересечения оси из сдвигается в точку .
- Это сдвигает весь график вниз, но форма графика остается неизменной.
б)
Построим график функции :
- Функция (обратный котангенс) также определена на всем множестве действительных чисел .
- График функции имеет вертикальные асимптоты при , стремясь к значениям для и для .
- График представляет собой гладкую кривую, которая асимптотически приближается к прямым и , проходя через точку .
Переместим график на 2 единицы влево вдоль оси абсцисс:
- Это означает замену на в функции, то есть:
- Сдвиг графика на 2 единицы влево приводит к тому, что точка пересечения оси из сдвигается в точку .
- График сдвигается влево, при этом форма графика остается неизменной.
Переместим график на единиц вверх вдоль оси ординат:
- Это означает добавление к выражению для , то есть:
- Сдвиг графика вверх на единиц приводит к тому, что каждая точка на графике сдвигается вверх на . Например, точка пересечения оси сдвигается в точку .
- Это сдвигает весь график вверх, но форма графика остаётся неизменной.