Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 21.52 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а)
б)
в)
г)
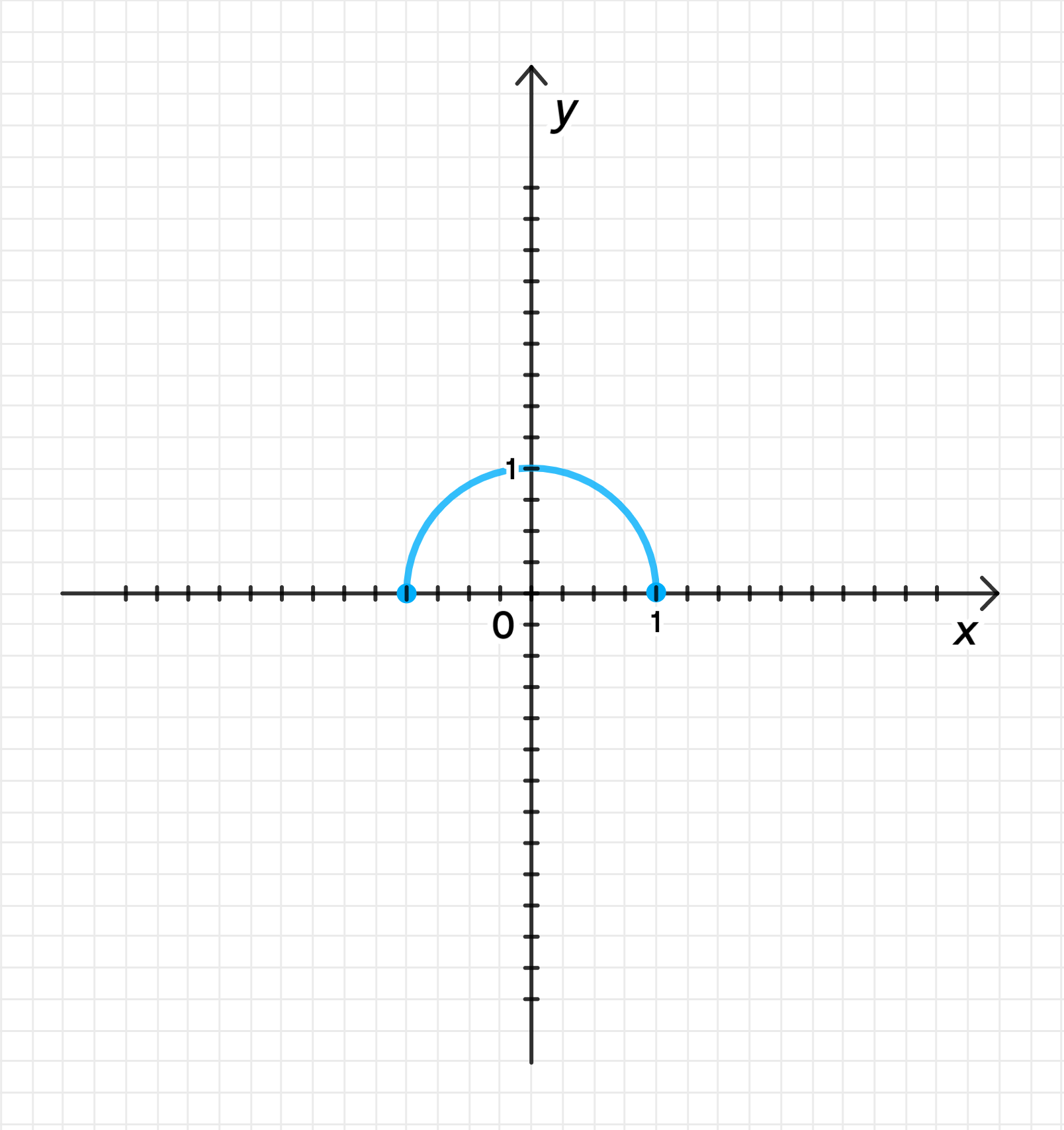
а) ;
— дуга полуокружности:
, , ;
График функции:
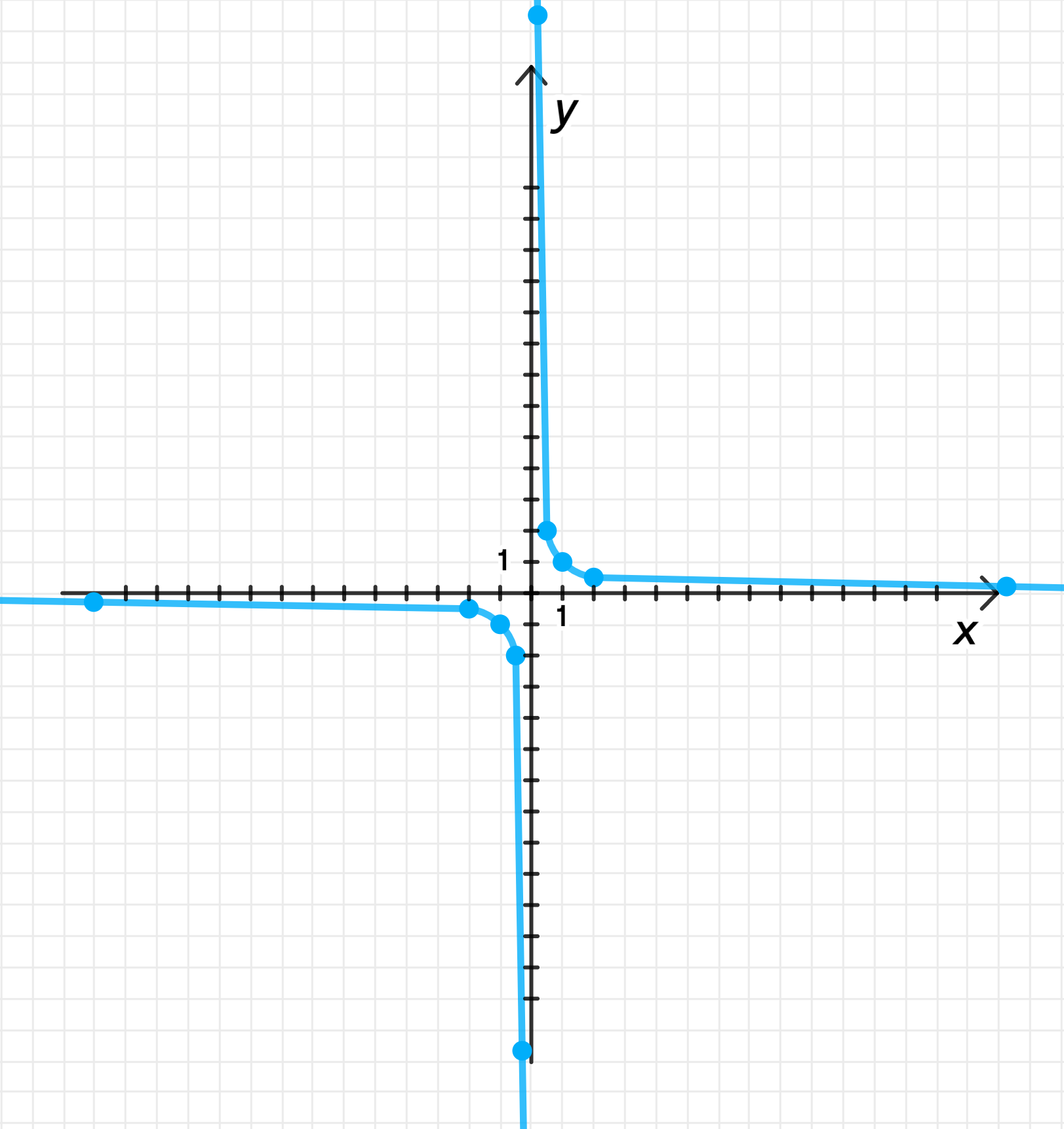
б) ;
— уравнение гиперболы:
, ;
Таблица значений:
График функции:
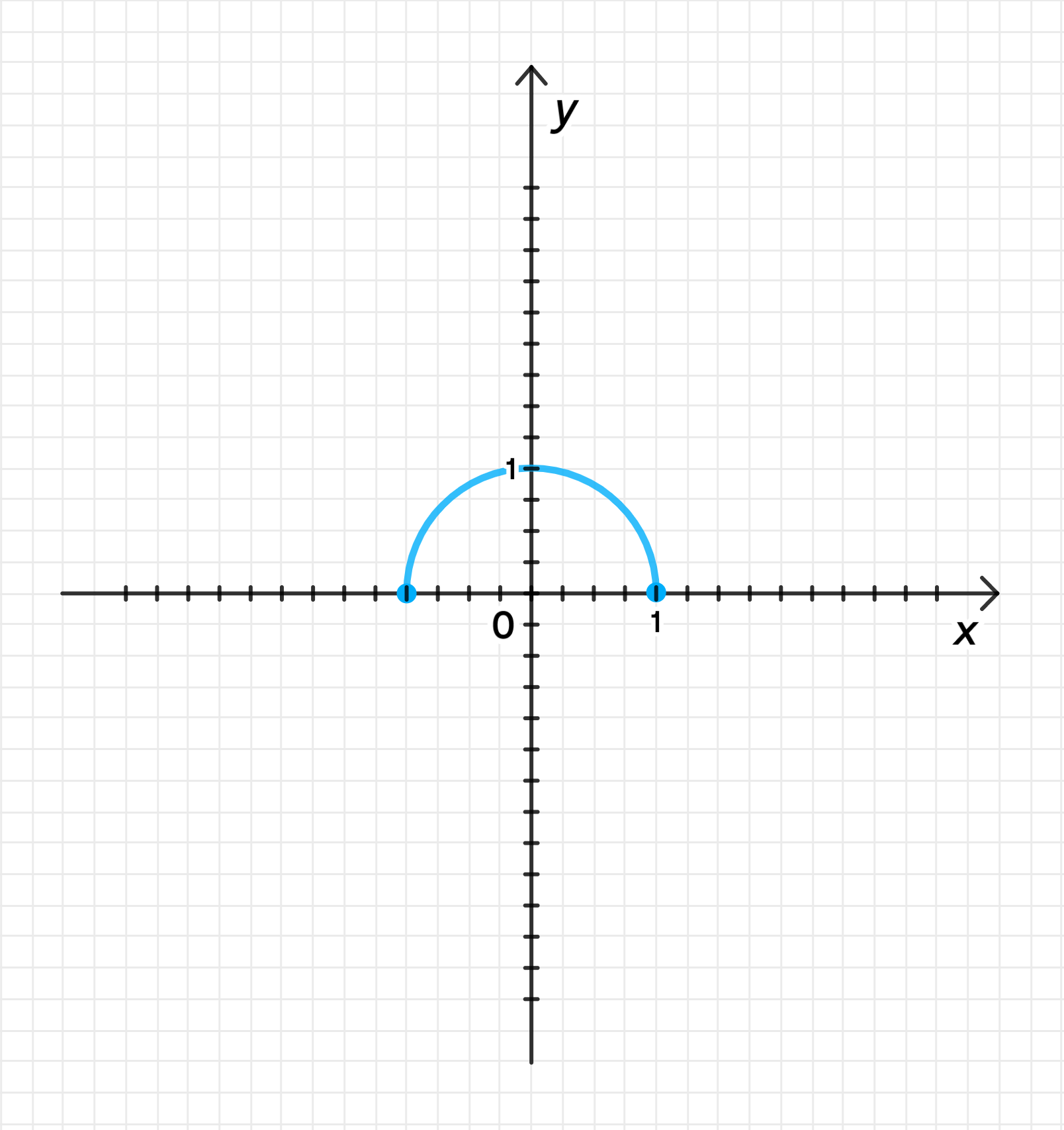
в) ;
— дуга полуокружности:
, , ;
График функции:
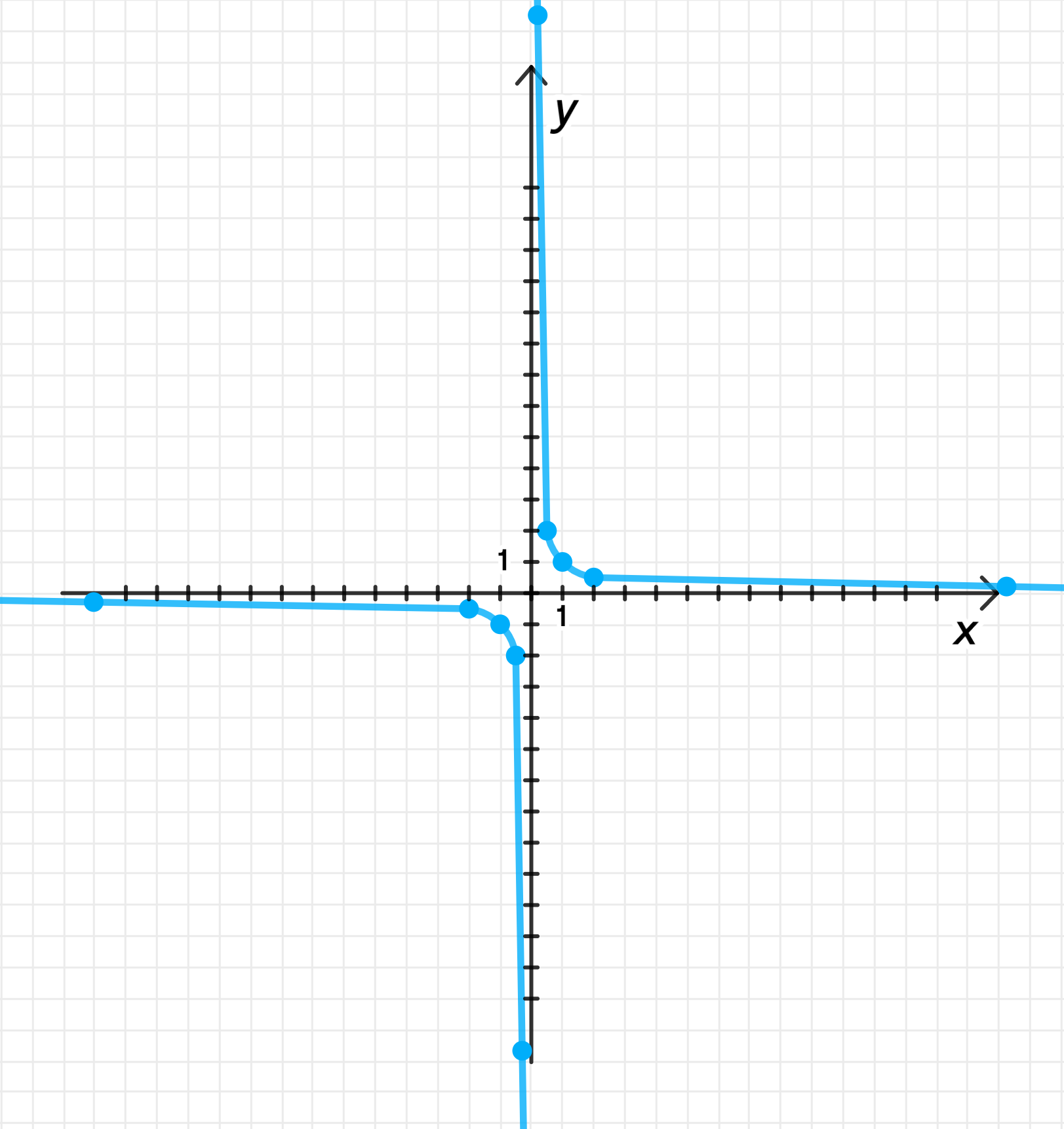
г) ;
— уравнение гиперболы:
, ;
Таблица значений:
График функции:
а)
Область определения:
- Арккосинус определен только для значений , так как принимает значения в пределах от -1 до 1.
- Следовательно, область определения функции также будет:
График функции:
- Функция выражается как , что является уравнением полуокружности радиусом 1, с центром в начале координат.
- Это выражение описывает верхнюю полукруглую часть окружности с радиусом 1, которая пересекает ось в точках и .
- График будет дугой полуокружности от точки до точки , с вершиной в точке .
б)
Область определения:
- Арккотангенс определен для всех действительных чисел , кроме нуля.
- Поскольку равно , область определения будет:
То есть, функция определена для всех действительных значений , за исключением .
График функции:
- График функции представляет собой гиперболу.
- Уравнение гиперболы имеет асимптоты, проходящие через оси и , а сама гипербола будет располагаться в первой и третьей четвертях.
- График функции будет иметь значения, стремящиеся к бесконечности при , и будет стремиться к нулю при или .
Таблица значений:
Это таблица значений функции , где для различных значений мы видим соответствующие значения .
в)
Область определения:
- Арксинус определен только для значений , так как может принимать значения только в пределах от -1 до 1.
- Следовательно, область определения функции будет:
График функции:
- Функция выражается как , что также является уравнением полуокружности радиусом 1.
- Это аналогично функции из пункта а), поскольку по сути мы также описываем верхнюю часть окружности с радиусом 1, где значения могут быть положительными от 0 до 1 для .
- График будет представлять собой дугу полуокружности, которая пересекает ось в точках и , а вершина будет в точке .
г)
Область определения:
- Арктангенс определен для всех , а котангенс также определен для всех , кроме .
- Следовательно, область определения функции будет:
График функции:
- График функции аналогичен графику, который был рассмотрен в пункте б), так как .
- Это также гипербола, которая имеет асимптоты через оси и .
- График функции будет находиться в первой и третьей четвертях, стремясь к бесконечности при и стремясь к нулю при или .
Таблица значений:
Это таблица значений функции , аналогичная таблице из пункта б).
Итоговые ответы:
а) , область определения: , график: дуга полуокружности радиусом 1.
б) , область определения: , график: гипербола .
в) , область определения: , график: дуга полуокружности радиусом 1.
г) , область определения: , график: гипербола .