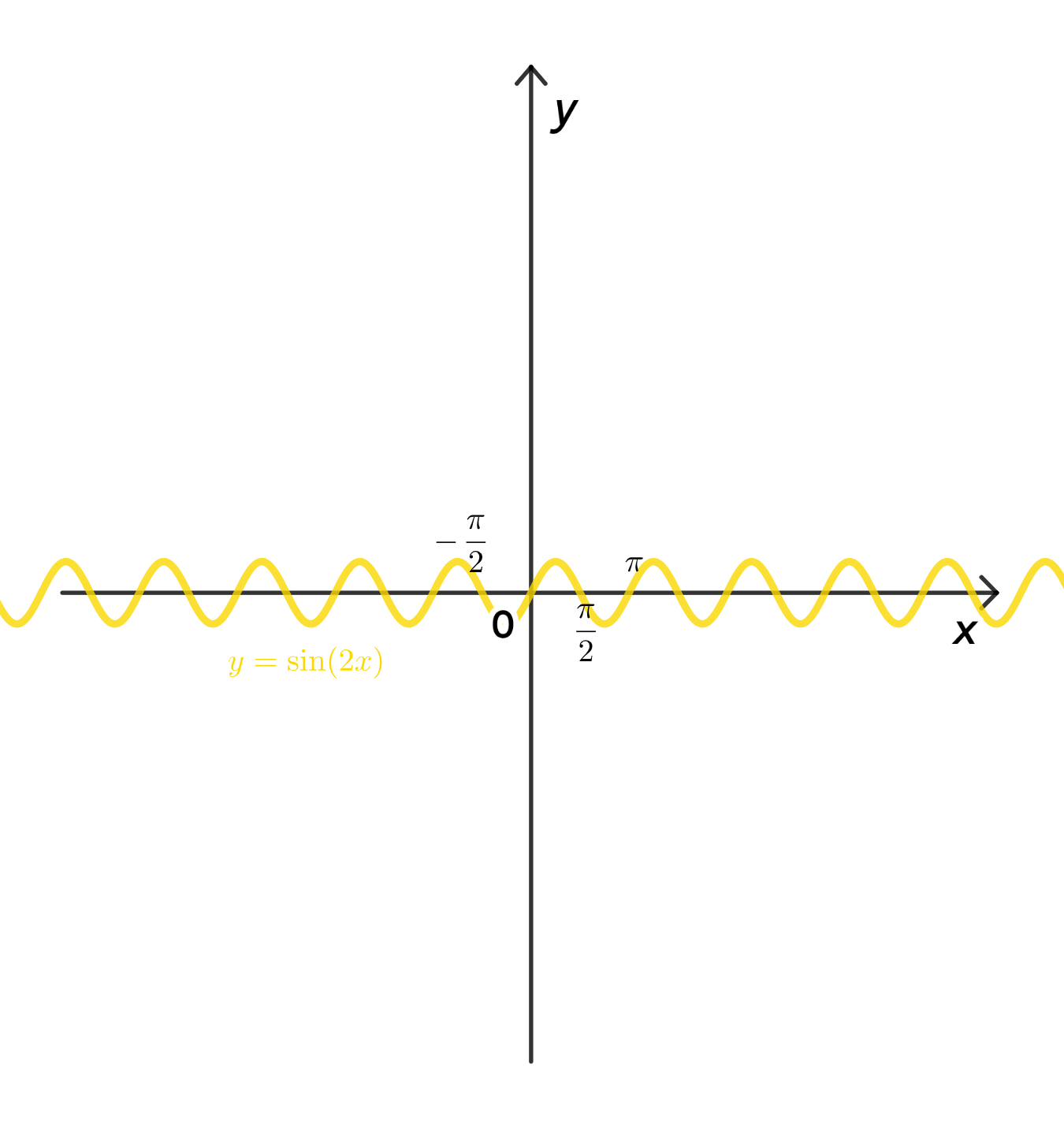ГДЗ Мордкович 10 Класс Профильный Уровень по Алгебре Задачник 📕 — Все Части

Алгебра Профильный Уровень

10 класс задачник профильный уровень Мордкович

10 класс

Тип

ГДЗ, Решебник.

Автор

А.Г. Мордкович, П. В. Семенов.

Год

2015-2020.

Издательство

Мнемозина.

Описание

Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.

ГДЗ по Алгебре 10 Класс Номер 24.48 Профильный Уровень Мордкович — Подробные Ответы

Задача

Постройте график функции:

а)

$y = \sin \frac{11 x}{5} \cdot \cos \frac{x + 10 π}{5} - \cos \frac{11 x}{5} \cdot \sin \frac{x}{5};$

б)

$y = \cos (2 x + \frac{7 π}{12}) \cdot \cos (x + \frac{π}{4}) + \sin (2 x + \frac{7 π}{12}) \cdot \sin (x + \frac{9 π}{4})$

Краткий ответ:

а)

$y = \sin \frac{11 x}{5} \cdot \cos \frac{x + 10 π}{5} - \cos \frac{11 x}{5} \cdot \sin \frac{x}{5};$ $y = \sin \frac{11 x}{5} \cdot \cos \frac{x}{5} - \cos \frac{11 x}{5} \cdot \sin \frac{x}{5} = \sin (\frac{11 x}{5} - \frac{x}{5}) = \sin \frac{10 x}{5} = \sin 2 x;$

Построим график функции $y = \sin x$ ;

Совершим его сжатие к оси ординат с коэффициентом $k = 2$ :

б)

$y = \cos (2 x + \frac{7 π}{12}) \cdot \cos (x + \frac{π}{4}) + \sin (2 x + \frac{7 π}{12}) \cdot \sin (x + \frac{9 π}{4});$ $y = \cos (2 x + \frac{7 π}{12}) \cdot \cos (x + \frac{π}{4}) + \sin (2 x + \frac{7 π}{12}) \cdot \sin (x + \frac{π}{4});$ $y = \cos ((2 x + \frac{7 π}{12}) - (x + \frac{π}{4})) = \cos (x + \frac{4 π}{12}) = \cos (x + \frac{π}{3});$

Построим график функции $y = \cos x$ ;

Переместим его на $\frac{π}{3}$ единиц влево вдоль оси абсцисс:

Подробный ответ:

а)

Исходное выражение:

$y = \sin \frac{11 x}{5} \cdot \cos \frac{x + 10 π}{5} - \cos \frac{11 x}{5} \cdot \sin \frac{x}{5} .$

Использование формулы приведения для синуса:

В данном выражении мы видим сумму произведений синуса и косинуса. Мы можем применить известную формулу приведения для синуса:

$\sin (A) \cdot \cos (B) - \cos (A) \cdot \sin (B) = \sin (A - B) .$

Теперь, применяя эту формулу к нашему выражению:

$y = \sin \frac{11 x}{5} \cdot \cos \frac{x + 10 π}{5} - \cos \frac{11 x}{5} \cdot \sin \frac{x}{5}$

мы получаем:

$y = \sin (\frac{11 x}{5} - \frac{x + 10 π}{5}) .$

Упрощаем выражение внутри синуса:

Теперь упростим выражение в скобках:

$\frac{11 x}{5} - \frac{x + 10 π}{5} = \frac{11 x - (x + 10 π)}{5} = \frac{11 x - x - 10 π}{5} =$

$= \frac{10 x - 10 π}{5} = \frac{10 (x - π)}{5} = 2 (x - π) .$

Таким образом, мы получаем:

$y = \sin (2 (x - π)) .$

Финальное преобразование:

Мы можем записать:

$y = \sin (2 x - 2 π) .$

Так как $\sin (2 x - 2 π) = \sin (2 x)$ (по свойствам синуса, так как синус имеет период $2 π$ ), получаем:

$y = \sin (2 x) .$

1) Построим график функции $y = \sin x$ :

График функции $y = \sin x$ — это периодическая волна с периодом $2 π$ и амплитудой 1. Начнем от $(0, 0)$ , потом график поднимется до 1 при $x = \frac{π}{2}$ , вернется в 0 при $x = π$ , опустится до -1 при $x = \frac{3 π}{2}$ и снова вернется в 0 при $x = 2 π$ .

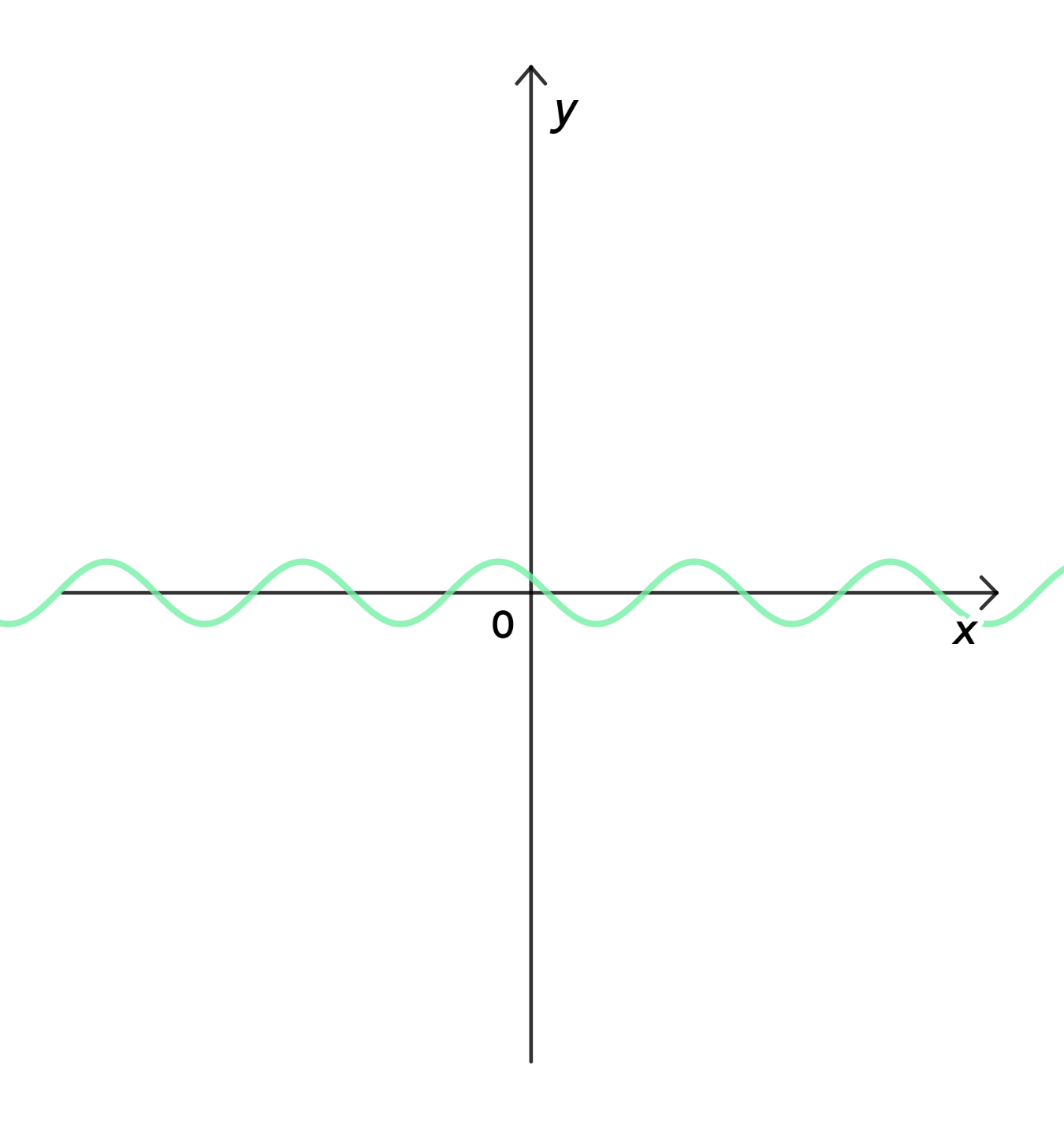
2) Совершим сжатие функции к оси ординат с коэффициентом $k = 2$ :

Функция $y = \sin (2 x)$ — это результат сжатия графика функции $y = \sin x$ к оси ординат на коэффициент 2, то есть теперь период функции будет равен $\frac{2 π}{2} = π$ . Таким образом, график функции $y = \sin (2 x)$ будет повторяться дважды за один период графика функции $y = \sin x$ .

б)

Исходное выражение:

$y = \cos (2 x + \frac{7 π}{12}) \cdot \cos (x + \frac{π}{4}) + \sin (2 x + \frac{7 π}{12}) \cdot \sin (x + \frac{9 π}{4}) .$

Использование формулы приведения для косинуса:

Снова применим формулу для косинуса:

$\cos A \cdot \cos B + \sin A \cdot \sin B = \cos (A - B) .$

Применяем эту формулу к нашему выражению:

$y = \cos (2 x + \frac{7 π}{12}) \cdot \cos (x + \frac{π}{4}) + \sin (2 x + \frac{7 π}{12}) \cdot \sin (x + \frac{9 π}{4})$

и получаем:

$y = \cos ((2 x + \frac{7 π}{12}) - (x + \frac{π}{4})) .$

Упрощаем выражение внутри косинуса:

Теперь упростим выражение в скобках:

$(2 x + \frac{7 π}{12}) - (x + \frac{π}{4}) = 2 x + \frac{7 π}{12} - x - \frac{π}{4} .$

Приводим подобные слагаемые:

$2 x - x = x, \frac{7 π}{12} - \frac{π}{4} = \frac{7 π}{12} - \frac{3 π}{12} = \frac{4 π}{12} = \frac{π}{3} .$

Таким образом, выражение внутри косинуса упрощается до:

$y = \cos (x + \frac{π}{3}) .$

1) Построим график функции $y = \cos x$ :

График функции $y = \cos x$ также периодичен, с периодом $2 π$ и амплитудой 1. Начнем от $(0, 1)$ , график затем спустится до -1 при $x = π$ , вернется в 1 при $x = 2 π$ и т. д.

2) Переместим его на $\frac{π}{3}$ единиц влево вдоль оси абсцисс:

Если мы перемещаем график функции $y = \cos x$ на $\frac{π}{3}$ единиц влево, то график функции $y = \cos (x + \frac{π}{3})$ будет сдвинут влево на $\frac{π}{3}$ единиц относительно исходного графика функции $y = \cos x$ . Это означает, что точка максимума, которая раньше была в $(0, 1)$ , теперь будет в $(- \frac{π}{3}, 1)$ , точка минимума будет в $(\frac{2 π}{3}, - 1)$ , и так далее.

Оцени решение