Краткий ответ:
а) y = sin ( 3 π + 3 x ) ⋅ sin ( 3 π 2 − x ) + sin ( π 2 + 3 x ) ⋅ sin ( 4 π − x ) + sin 99 π 2
y = − sin 3 x ⋅ ( − cos x ) + cos 3 x ⋅ ( − sin x ) + sin ( 50 π − π 2 ) ; y = -\sin 3x \cdot (-\cos x) + \cos 3x \cdot (-\sin x) + \sin\left(50\pi — \frac{\pi}{2}\right);
y = sin 3 x ⋅ cos x − cos 3 x ⋅ sin x − sin π 2 ; y = \sin 3x \cdot \cos x — \cos 3x \cdot \sin x — \sin \frac{\pi}{2};
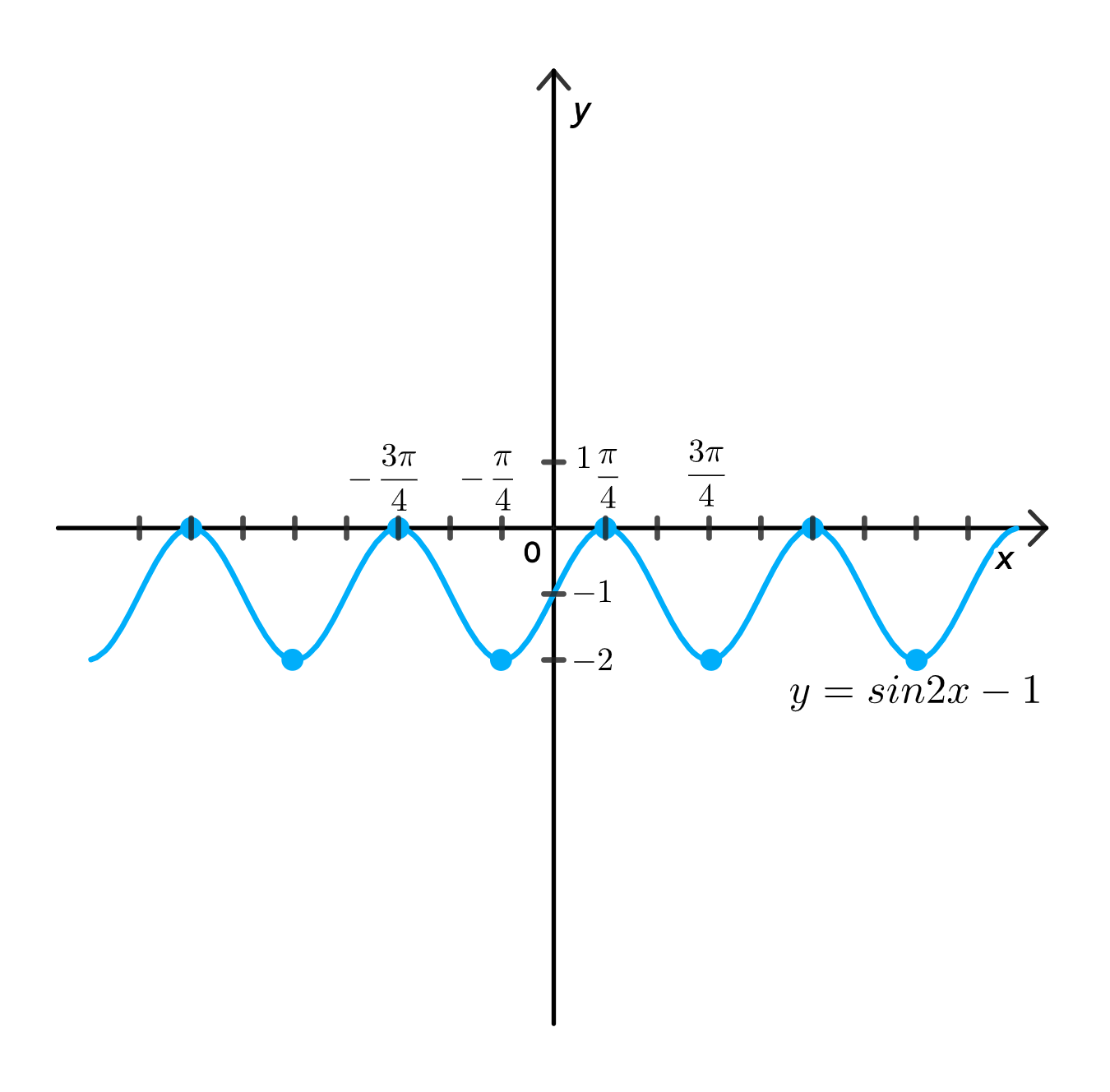
y = sin ( 3 x − x ) − 1 = sin 2 x − 1 ; y = \sin(3x — x) — 1 = \sin 2x — 1;
1) Построим одну дугу графика функции y = sin x y = \sin x
Совершим ее сжатие к оси O y Oy k = 2 k = 2 Переместим ее на 1 единицу вниз вдоль оси ординат; 2) Достроим график функции:
б) y = cos ( π + x ) ⋅ cos ( 3 π − x 2 ) − cos ( π 2 + x ) ⋅ cos 3 π + x 2 + cos 16 π 3
y = − cos x ⋅ ( − cos x 2 ) − ( − sin x ) ⋅ cos ( 3 π 2 + x 2 ) + cos ( 5 π + π 3 ) ; y = -\cos x \cdot \left(-\cos \frac{x}{2}\right) — (-\sin x) \cdot \cos\left(\frac{3\pi}{2} + \frac{x}{2}\right) + \cos\left(5\pi + \frac{\pi}{3}\right);
y = cos x ⋅ cos x 2 + sin x ⋅ sin x 2 − cos π 3 ; y = \cos x \cdot \cos \frac{x}{2} + \sin x \cdot \sin \frac{x}{2} — \cos \frac{\pi}{3};
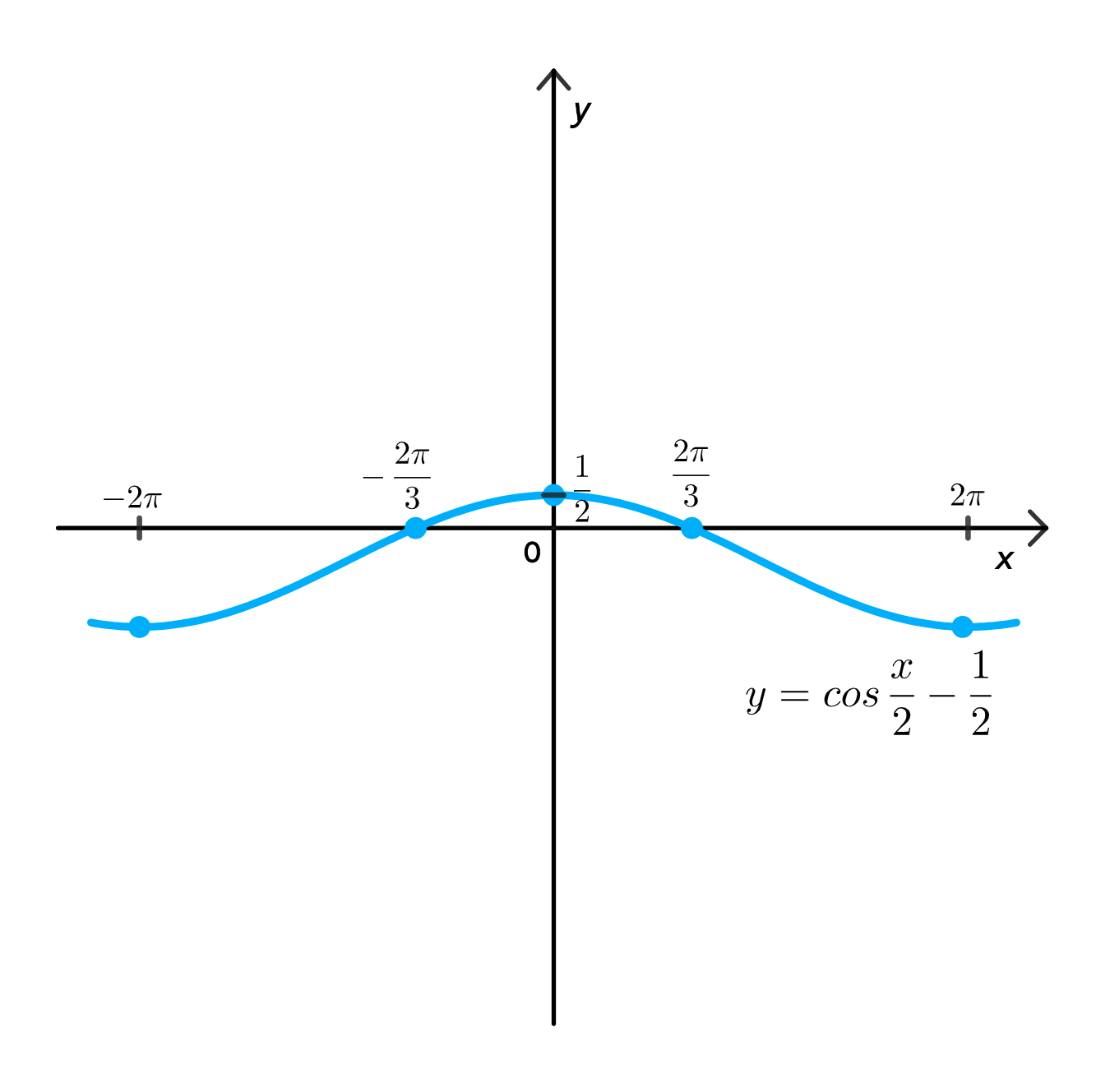
y = cos ( x − x 2 ) − 1 2 = cos x 2 − 1 2 ; y = \cos\left(x — \frac{x}{2}\right) — \frac{1}{2} = \cos \frac{x}{2} — \frac{1}{2};
1) Построим одну дугу графика функции y = cos x y = \cos x
Совершим ее растяжение от оси O y Oy k = 2 k = 2 Переместим ее на 0,5 единицы вниз вдоль оси ординат; 2) Достроим график функции:
Подробный ответ:
а)
Имеем выражение:
y = sin ( 3 π + 3 x ) ⋅ sin ( 3 π 2 − x ) + sin ( π 2 + 3 x ) ⋅ sin ( 4 π − x ) + sin 99 π 2 y = \sin(3\pi + 3x) \cdot \sin\left(\frac{3\pi}{2} — x\right) + \sin\left(\frac{\pi}{2} + 3x\right) \cdot \sin(4\pi — x) + \sin\frac{99\pi}{2}
Шаг 1: Упрощение тригонометрических выражений
Первая часть:
sin ( 3 π + 3 x ) = − sin 3 x (так как sin ( θ + π ) = − sin θ ) \sin(3\pi + 3x) = -\sin 3x \quad \text{(так как } \sin(\theta + \pi) = -\sin \theta\text{)} sin ( 3 π 2 − x ) = − cos x (формула: sin ( 3 π 2 − x ) = − cos x ) \sin\left(\frac{3\pi}{2} — x\right) = -\cos x \quad \text{(формула: } \sin\left(\frac{3\pi}{2} — x\right) = -\cos x\text{)}
Значит:
sin ( 3 π + 3 x ) ⋅ sin ( 3 π 2 − x ) = ( − sin 3 x ) ⋅ ( − cos x ) = sin 3 x ⋅ cos x \sin(3\pi + 3x) \cdot \sin\left(\frac{3\pi}{2} — x\right) = (-\sin 3x) \cdot (-\cos x) = \sin 3x \cdot \cos x
Вторая часть:
sin ( π 2 + 3 x ) = cos 3 x (формула: sin ( π 2 + x ) = cos x ) \sin\left(\frac{\pi}{2} + 3x\right) = \cos 3x \quad \text{(формула: } \sin\left(\frac{\pi}{2} + x\right) = \cos x\text{)} sin ( 4 π − x ) = − sin x (формула: sin ( 2 π − x ) = − sin x , т.к. 4π кратно 2π) \sin(4\pi — x) = -\sin x \quad \text{(формула: } \sin(2\pi — x) = -\sin x\text{, т.к. 4π кратно 2π)}
Значит:
sin ( π 2 + 3 x ) ⋅ sin ( 4 π − x ) = cos 3 x ⋅ ( − sin x ) = − cos 3 x ⋅ sin x \sin\left(\frac{\pi}{2} + 3x\right) \cdot \sin(4\pi — x) = \cos 3x \cdot (-\sin x) = -\cos 3x \cdot \sin x
Третья часть:
sin ( 99 π 2 ) \sin\left(\frac{99\pi}{2}\right)
Упростим:
99 π 2 = 100 π 2 − π 2 = 50 π − π 2 \frac{99\pi}{2} = \frac{100\pi}{2} — \frac{\pi}{2} = 50\pi — \frac{\pi}{2}
Поскольку sin ( 2 π n − x ) = − sin x \sin(2\pi n — x) = -\sin x
sin ( 50 π − π 2 ) = − sin ( π 2 ) = − 1 \sin\left(50\pi — \frac{\pi}{2}\right) = -\sin\left(\frac{\pi}{2}\right) = -1
Шаг 2: Собираем все
y = sin 3 x ⋅ cos x − cos 3 x ⋅ sin x − 1 y = \sin 3x \cdot \cos x — \cos 3x \cdot \sin x — 1
Шаг 3: Используем формулу разности синусов
sin A ⋅ cos B − cos A ⋅ sin B = sin ( A − B ) \sin A \cdot \cos B — \cos A \cdot \sin B = \sin(A — B)
Применим:
y = sin ( 3 x − x ) − 1 = sin 2 x − 1 y = \sin(3x — x) — 1 = \sin 2x — 1
График: y = sin 2 x − 1 y = \sin 2x — 1
1. Построение базовой функции y = sin x y = \sin x
Функция периодическая, период: 2 π 2\pi Амплитуда: 1 Значения: от -1 до 1 2. Преобразования
Сжатие к оси O y Oy k = 2 k = 2 y = sin 2 x y = \sin 2x
T = 2 π 2 = π T = \frac{2\pi}{2} = \pi
Смещение на 1 вниз вдоль оси ординат
y = sin 2 x − 1 y = \sin 2x — 1
3. Итог
Функция y = sin 2 x − 1 y = \sin 2x — 1
Сжатый в 2 раза по оси X синус Сдвинут на 1 вниз Значения: от -2 до 0 Период: π \pi
б)
Дано:
y = cos ( π + x ) ⋅ cos ( 3 π − x 2 ) − cos ( π 2 + x ) ⋅ cos ( 3 π + x 2 ) + cos ( 16 π 3 ) y = \cos(\pi + x) \cdot \cos\left(3\pi — \frac{x}{2}\right) — \cos\left(\frac{\pi}{2} + x\right) \cdot \cos\left(\frac{3\pi + x}{2}\right) + \cos\left(\frac{16\pi}{3}\right)
Шаг 1: Упрощение
Первая часть:
cos ( π + x ) = − cos x \cos(\pi + x) = -\cos x cos ( 3 π − x 2 ) = − cos x 2 \cos\left(3\pi — \frac{x}{2}\right) = -\cos \frac{x}{2}
(аналогично, т.к. cos ( π + α ) = − cos α \cos(\pi + \alpha) = -\cos \alpha
Итак:
cos ( π + x ) ⋅ cos ( 3 π − x 2 ) = ( − cos x ) ⋅ ( − cos x 2 ) = cos x ⋅ cos x 2 \cos(\pi + x) \cdot \cos\left(3\pi — \frac{x}{2}\right) = (-\cos x) \cdot (-\cos \frac{x}{2}) = \cos x \cdot \cos \frac{x}{2}
Вторая часть:
cos ( π 2 + x ) = − sin x \cos\left(\frac{\pi}{2} + x\right) = -\sin x cos ( 3 π + x 2 ) = cos ( 3 π 2 + x 2 ) \cos\left(\frac{3\pi + x}{2}\right) = \cos\left(\frac{3\pi}{2} + \frac{x}{2}\right)
Формула:
cos ( 3 π 2 + x 2 ) = sin ( x 2 ) ⋅ ( − 1 ) \cos\left(\frac{3\pi}{2} + \frac{x}{2}\right) = \sin\left(\frac{x}{2}\right) \cdot (-1)
(т.к. cos ( 3 π 2 + x ) = − sin x \cos\left(\frac{3\pi}{2} + x\right) = -\sin x
Итак:
− sin x ⋅ ( − sin x 2 ) = sin x ⋅ sin x 2 -\sin x \cdot (-\sin \frac{x}{2}) = \sin x \cdot \sin \frac{x}{2}
Третья часть:
cos ( 16 π 3 ) \cos\left(\frac{16\pi}{3}\right)
Приведем к основному углу:
16 π 3 = 2 π ⋅ 8 3 = 2 π ⋅ 2 + 2 π 3 ⇒ cos ( 16 π 3 ) = cos ( 2 π 3 ) = − 1 2 \frac{16\pi}{3} = 2\pi \cdot \frac{8}{3} = 2\pi \cdot 2 + \frac{2\pi}{3} \Rightarrow \cos\left(\frac{16\pi}{3}\right) = \cos\left(\frac{2\pi}{3}\right) = -\frac{1}{2}
Шаг 2: Собираем
y = cos x ⋅ cos x 2 + sin x ⋅ sin x 2 − 1 2 y = \cos x \cdot \cos \frac{x}{2} + \sin x \cdot \sin \frac{x}{2} — \frac{1}{2}
Шаг 3: Используем формулу косинуса разности
cos A ⋅ cos B + sin A ⋅ sin B = cos ( A − B ) \cos A \cdot \cos B + \sin A \cdot \sin B = \cos(A — B)
Значит:
y = cos ( x − x 2 ) − 1 2 = cos ( x 2 ) − 1 2 y = \cos\left(x — \frac{x}{2}\right) — \frac{1}{2} = \cos\left(\frac{x}{2}\right) — \frac{1}{2}
График: y = cos ( x 2 ) − 1 2 y = \cos\left(\frac{x}{2}\right) — \frac{1}{2}
1. Базовая функция y = cos x y = \cos x
Период: 2 π 2\pi Амплитуда: 1 Значения: от -1 до 1 2. Преобразования
Растяжение от оси O y Oy k = 2 k = 2 y = cos ( x 2 ) y = \cos\left(\frac{x}{2}\right)
T = 2 π 1 / 2 = 4 π T = \frac{2\pi}{1/2} = 4\pi
Смещение на 0.5 вниз
y = cos ( x 2 ) − 1 2 y = \cos\left(\frac{x}{2}\right) — \frac{1}{2}
3. Итог
Функция y = cos ( x 2 ) − 1 2 y = \cos\left(\frac{x}{2}\right) — \frac{1}{2}
Период: 4 π 4\pi Значения: от − 1.5 -1.5 0.5 0.5 График — волнообразный, растянут по оси x x