Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 27.70 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а)
б)
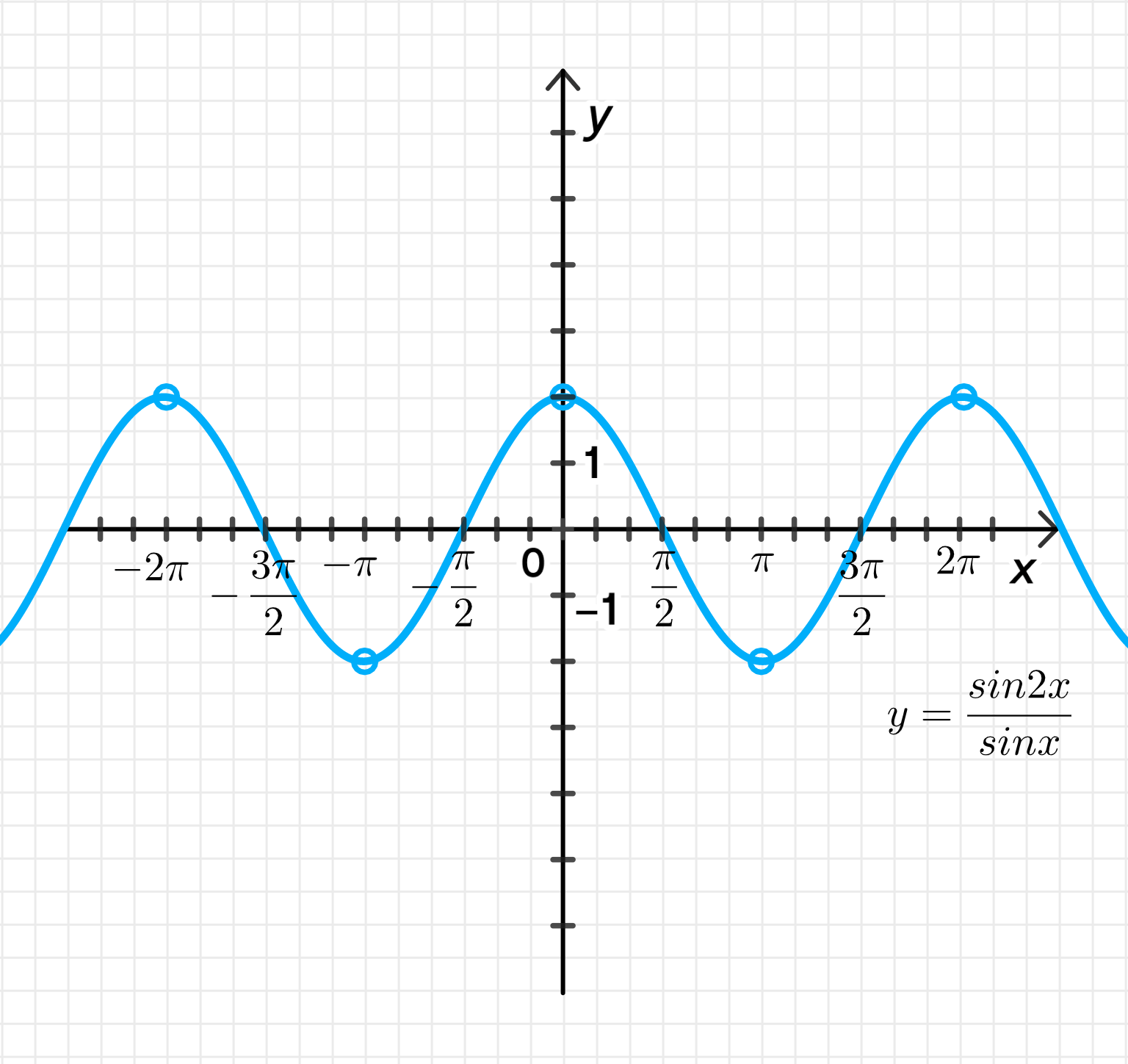
а) ;
Выражение имеет смысл при:
Построим график функции ;
Совершим его растяжение от оси с коэффициентом :
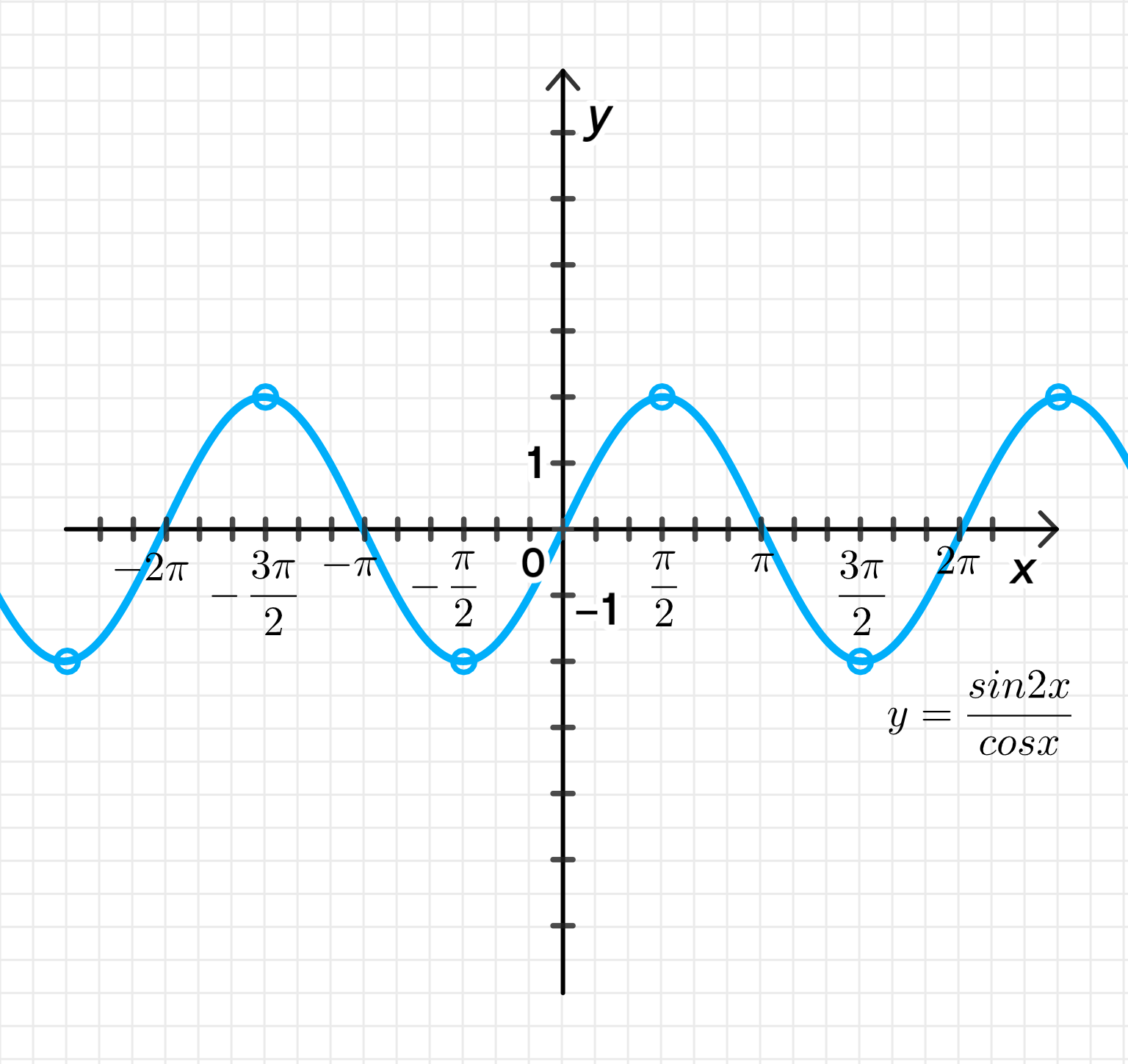
б) ;
Выражение имеет смысл при:
Построим график функции ;
Совершим его растяжение от оси с коэффициентом :
а)
Преобразуем выражение:
У нас есть выражение . Для того чтобы упростить его, мы воспользуемся формулой для синуса двойного угла:
Таким образом, подставляем это в выражение для :
У нас сокращаются в числителе и знаменателе:
Таким образом, мы получаем, что функция равна .
Условия, при которых выражение имеет смысл:
Рассмотрим выражение . Оно имеет смысл только тогда, когда , поскольку деление на ноль невозможно. Вспоминаем, что при , где — целое число. Таким образом, выражение имеет смысл при:
Построение графика функции :
Мы знаем, что график функции представляет собой периодическую кривую с амплитудой 1 и периодом . График функции будет аналогичен графику функции , но растянут по оси в два раза, так как перед косинусом стоит коэффициент 2. Таким образом, амплитуда функции удваивается, а период остается равным .
- Функция будет колебаться между значениями и .
- График будет иметь тот же вид, что и график функции , но его максимумы будут равны 2, а минимумы — -2.
Растяжение графика от оси с коэффициентом :
Означает, что график функции будет растянут по вертикали в два раза. Таким образом, максимальное значение функции будет равно 2, а минимальное — -2. Период графика останется , так как коэффициент касается только вертикального растяжения.
б)
Преобразуем выражение:
У нас есть выражение . Мы можем снова воспользоваться формулой для синуса двойного угла:
Подставляем это в исходное выражение для :
У нас снова сокращаются в числителе и знаменателе:
Таким образом, мы получаем, что функция равна .
Условия, при которых выражение имеет смысл:
Рассмотрим выражение . Оно имеет смысл только тогда, когда , поскольку деление на ноль невозможно. Вспоминаем, что при , где — целое число. Таким образом, выражение имеет смысл при:
Построение графика функции :
График функции представляет собой периодическую кривую с амплитудой 1 и периодом . График функции будет аналогичен графику функции , но растянут по оси в два раза, так как перед синусом стоит коэффициент 2. Таким образом, амплитуда функции удваивается, а период остается равным .
- Функция будет колебаться между значениями и .
- График будет иметь тот же вид, что и график функции , но его максимумы будут равны 2, а минимумы — -2.
Растяжение графика от оси с коэффициентом :
Растяжение по оси с коэффициентом означает, что максимальное значение функции будет равно 2, а минимальное — -2. Период графика останется , так как коэффициент касается только вертикального растяжения.