ГДЗ Мордкович 10 Класс Профильный Уровень по Алгебре Задачник 📕 — Все Части

Алгебра Профильный Уровень

10 класс задачник профильный уровень Мордкович

10 класс

Тип

ГДЗ, Решебник.

Автор

А.Г. Мордкович, П. В. Семенов.

Год

2015-2020.

Издательство

Мнемозина.

Описание

Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.

ГДЗ по Алгебре 10 Класс Номер 29.29 Профильный Уровень Мордкович — Подробные Ответы

Задача

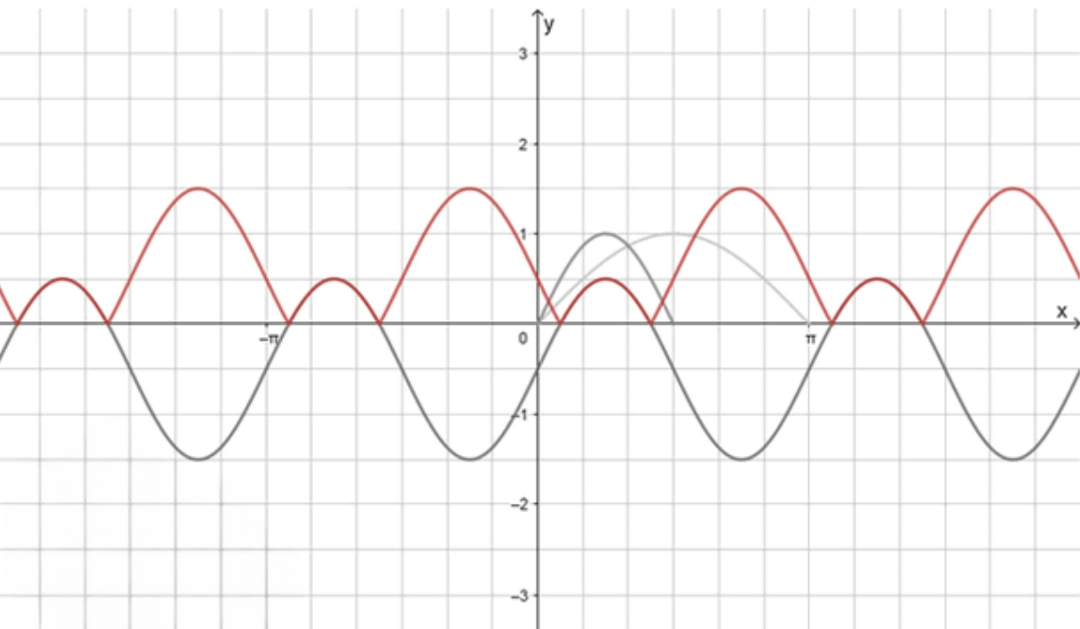
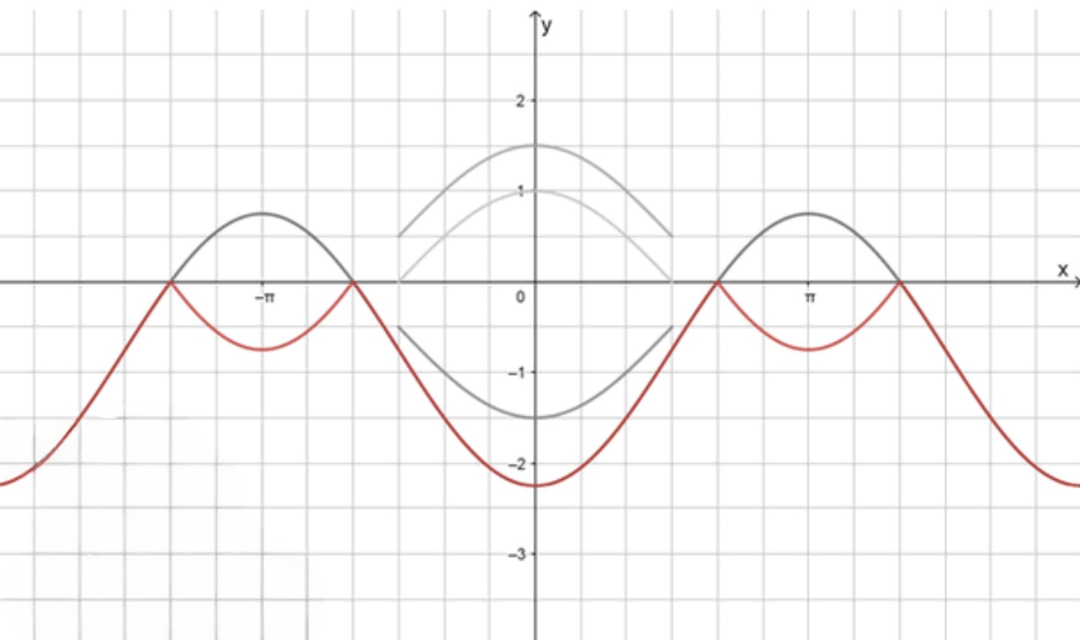
Постройте график функции:

а) $y = 2 ∣ \sin (x - \frac{5 π}{12}) \cdot \cos (x + \frac{5 π}{12}) ∣$

б) $y = - 3 ∣ \cos \frac{3 x + π}{6} \cdot \cos \frac{3 x - π}{6} ∣$

Краткий ответ:

а) $y = 2 ∣ \sin (x - \frac{5 π}{12}) \cdot \cos (x + \frac{5 π}{12}) ∣;$

$y = 2 \cdot \frac{1}{2} ∣ \sin ((x - \frac{5 π}{12}) + (x + \frac{5 π}{12})) + \sin ((x - \frac{5 π}{12}) - (x + \frac{5 π}{12})) ∣;$

$y = ∣ \sin 2 x + \sin \frac{- 10 π}{12} ∣ = ∣ \sin 2 x - \sin \frac{5 π}{6} ∣ = ∣ \sin 2 x - \frac{1}{2} ∣;$

1) Построим одну дугу графика функции $y = \sin x$ , а затем:

Совершим ее сжатие к оси $O y$ с коэффициентом $k = 2$ ;
Переместим ее на $0, 5$ единиц вниз вдоль оси ординат;
Достроим график функции;

2) Отразим относительно оси $O x$ часть графика, лежащую под ней:

б) $y = - 3 ∣ \cos \frac{3 x + π}{6} \cdot \cos \frac{3 x - π}{6} ∣;$

$y = - 3 \cdot \frac{1}{2} ∣ \cos (\frac{3 x + π}{6} + \frac{3 x - π}{6}) + \cos (\frac{3 x + π}{6} - \frac{3 x - π}{6}) ∣;$

$y = - \frac{3}{2} ∣ \cos \frac{6 x}{6} + \cos \frac{2 π}{6} ∣ = - \frac{3}{2} ∣ \cos x + \cos \frac{π}{3} ∣ = - \frac{3}{2} ∣ \cos x + \frac{1}{2} ∣;$

1) Построим одну дугу графика функции $y = \cos x$ , а затем:

Переместим ее на $0, 5$ единиц вверх вдоль оси ординат;
Отразим ее относительно оси абсцисс;
Совершим ее растяжение от оси $O x$ с коэффициентом $k = 1, 5$ ;
Достроим график функции;

2) Отразим относительно оси $O x$ часть графика, лежащую над ней:

Подробный ответ:

а) $y = 2 ∣ \sin (x - \frac{5 π}{12}) \cdot \cos (x + \frac{5 π}{12}) ∣$

Шаг 1: Преобразование выражения

Начнем с использования тригонометрической формулы для произведения синуса и косинуса:

$\sin A \cdot \cos B = \frac{1}{2} (\sin (A + B) + \sin (A - B))$

Подставим $A = x - \frac{5 π}{12}$ и $B = x + \frac{5 π}{12}$ :

$\sin (x - \frac{5 π}{12}) \cdot \cos (x + \frac{5 π}{12}) = \frac{1}{2} (\sin ((x - \frac{5 π}{12}) +$

$+ (x + \frac{5 π}{12})) + \sin ((x - \frac{5 π}{12}) - (x + \frac{5 π}{12})))$

Упростим аргументы синусов:

$(x - \frac{5 π}{12}) + (x + \frac{5 π}{12}) = 2 x$
$(x - \frac{5 π}{12}) - (x + \frac{5 π}{12}) = - \frac{10 π}{12} = - \frac{5 π}{6}$

Тогда:

$y = 2 \cdot \frac{1}{2} ∣ \sin 2 x + \sin (- \frac{5 π}{6}) ∣$

Так как $\sin (- θ) = - \sin θ$ , получаем:

$y = ∣ \sin 2 x - \sin \frac{5 π}{6} ∣$

Известно, что $\sin \frac{5 π}{6} = \frac{1}{2}$ , поэтому:

$y = ∣ \sin 2 x - \frac{1}{2} ∣$

Это окончательное преобразование функции. Теперь мы можем исследовать график этой функции.

Шаг 2: Построение графика

Построение графика функции $y = \sin x$ :
Построим одну дугу синусоиды, которая имеет период $2 π$ . Для этого определим несколько точек на графике функции $y = \sin x$ в интервале от $0$ до $π$ , так как это будет одна дуга.
Сжатие графика к оси $O y$ с коэффициентом $k = 2$ :
Умножим значения функции $y = \sin x$ на 2, что приведет к растяжению графика по оси $y$ с коэффициентом 2. То есть все значения функции будут удвоены.
Перемещение графика на 0,5 единиц вниз:
Теперь перенесем график вниз вдоль оси $y$ на 0,5 единиц. Для этого из всех значений функции $y$ вычитаем 0,5.
Достроение графика:
После выполнения этих операций получаем преобразованный график.
Отражение относительно оси $O x$ части графика, лежащей под ней:
Все точки графика, находящиеся ниже оси $O x$ , отражаются относительно этой оси, то есть их $y$ -координаты становятся положительными.

б) $y = - 3 ∣ \cos \frac{3 x + π}{6} \cdot \cos \frac{3 x - π}{6} ∣$

Шаг 1: Преобразование выражения

Используем ту же формулу для произведения косинусов:

$\cos A \cdot \cos B = \frac{1}{2} (\cos (A + B) + \cos (A - B))$

Подставим $A = \frac{3 x + π}{6}$ и $B = \frac{3 x - π}{6}$ :

$\cos \frac{3 x + π}{6} \cdot \cos \frac{3 x - π}{6} = \frac{1}{2} (\cos (\frac{3 x + π}{6} + \frac{3 x - π}{6}) + \cos (\frac{3 x + π}{6} - \frac{3 x - π}{6}))$

Упростим аргументы косинусов:

$\frac{3 x + π}{6} + \frac{3 x - π}{6} = \frac{6 x}{6} = x$
$\frac{3 x + π}{6} - \frac{3 x - π}{6} = \frac{2 π}{6} = \frac{π}{3}$

Тогда:

$y = - 3 \cdot \frac{1}{2} ∣ \cos x + \cos \frac{π}{3} ∣$

Так как $\cos \frac{π}{3} = \frac{1}{2}$ , получаем:

$y = - \frac{3}{2} ∣ \cos x + \frac{1}{2} ∣$

Это окончательное преобразование функции. Теперь рассмотрим, как будет выглядеть график этой функции.

Шаг 2: Построение графика

Построение графика функции $y = \cos x$ :
Построим одну дугу косинусоиды, которая имеет период $2 π$ .
Перемещение графика на 0,5 единиц вверх:
Мы перемещаем весь график вверх на 0,5 единицы вдоль оси $y$ .
Отражение относительно оси абсцисс:
Отразим весь график относительно оси $O x$ , то есть инвертируем знаки всех значений функции.
Растяжение графика от оси $O x$ с коэффициентом $k = 1, 5$ :
Умножим все значения функции на коэффициент $k = 1, 5$ , что растянет график по вертикали.
Достроение графика:
После всех преобразований мы получим график функции.
Отражение относительно оси $O x$ части графика, лежащей над ней:
Все точки, расположенные выше оси $O x$ , будут отражены относительно этой оси.

Оцени решение