Краткий ответ:
Дано уравнение:
z ‾ + 1 = 1 z + 1 ; \overline{z} + 1 = \frac{1}{z + 1}; ( z ‾ + 1 ) ( z + 1 ) = 1 ; (\overline{z} + 1)(z + 1) = 1; z ‾ z + z ‾ + z + 1 = 1 ; \overline{z}z + \overline{z} + z + 1 = 1; z ‾ z + z ‾ + z = 0 ; \overline{z}z + \overline{z} + z = 0; ( x − y i ) ( x + y i ) + ( x − y i ) + ( x + y i ) = 0 ; (x — yi)(x + yi) + (x — yi) + (x + yi) = 0; x 2 − y 2 i + x − y i + x + y i = 0 ; x^2 — y^2i + x — yi + x + yi = 0; x 2 + y 2 + 2 x = 0 ; x^2 + y^2 + 2x = 0; x 2 + 2 x + 1 + y 2 − 1 = 0 ; x^2 + 2x + 1 + y^2 — 1 = 0; ( x + 1 ) 2 + y 2 = 1 ; (x + 1)^2 + y^2 = 1;
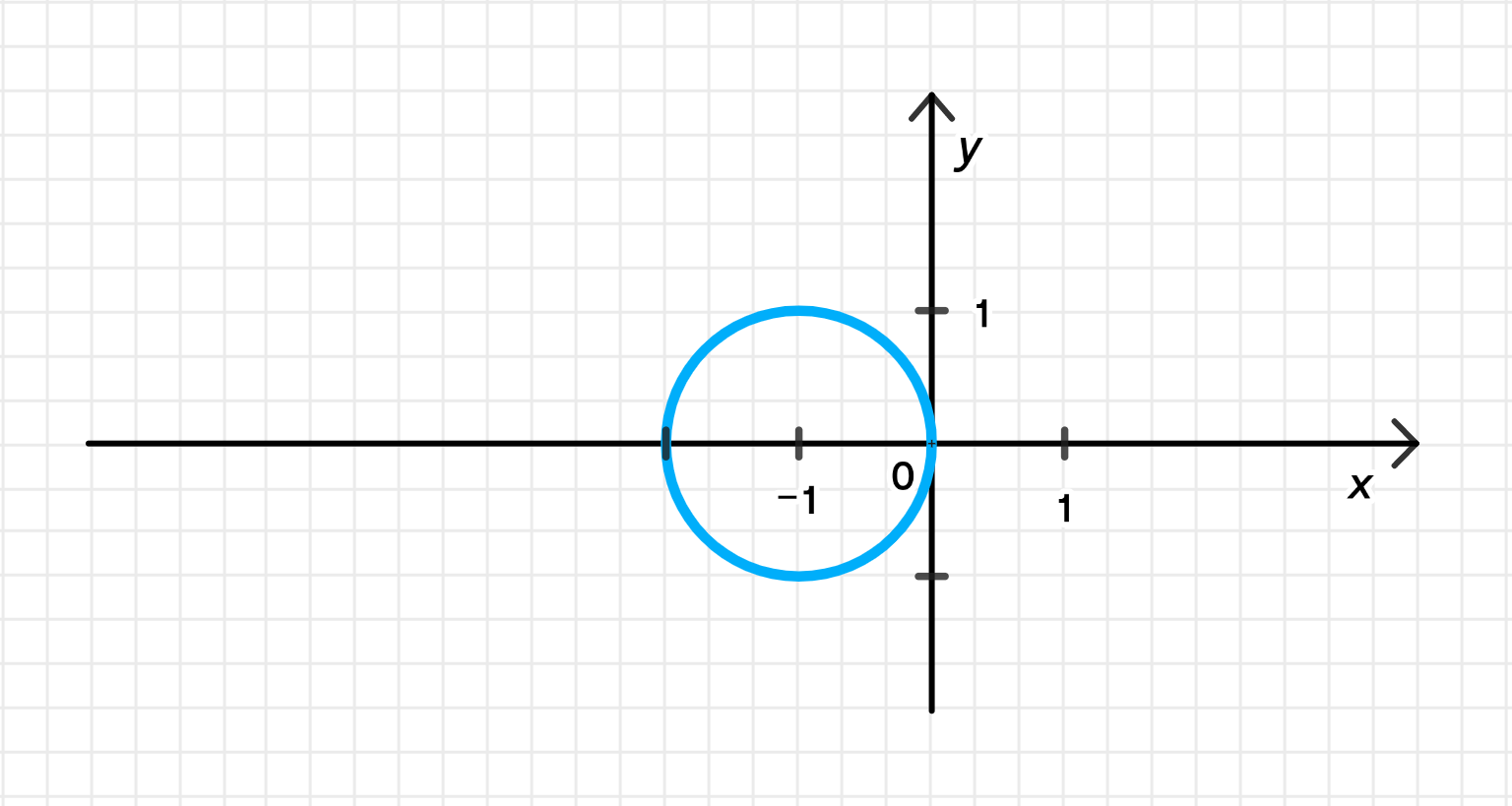
Множество решений на координатной плоскости:
x 0 = − 1 , y 0 = 0 , R = 1 ;
x_0 = -1, \; y_0 = 0, \; R = 1;
а) Корень, у которого действительная часть наименьшая:
x = − 2 , y = 0 ; x = -2, \; y = 0;
Ответ: z = − 2 z = -2
б) Корень, у которого мнимая часть наименьшая:
x = − 1 , y = − 1 ; x = -1, \; y = -1;
Ответ: z = − 1 − i z = -1 — i
в) Корень, который ближе всего расположен к началу координат:
x = 0 , y = 0 ; x = 0, \; y = 0;
Ответ: 0 0
г) Корень, который ближе всего расположен к числу i i
a = tg π 4 = π 4 ; a = \operatorname{tg} \frac{\pi}{4} = \frac{\pi}{4}; x = cos π 4 − 1 = 1 2 − 1 = 1 − 2 2 ; x = \cos \frac{\pi}{4} — 1 = \frac{1}{\sqrt{2}} — 1 = \frac{1 — \sqrt{2}}{\sqrt{2}}; y = sin π 4 = 1 2 ; y = \sin \frac{\pi}{4} = \frac{1}{\sqrt{2}};
Ответ: z = 1 − 2 + i 2 z = \frac{1 — \sqrt{2} + i}{\sqrt{2}}
Подробный ответ:
Шаг 1. Исходное уравнение
z ‾ + 1 = 1 z + 1 \overline{z} + 1 = \frac{1}{z + 1}
Шаг 2. Представление z z z = x + i y z = x + iy
Пусть:
z = x + i y , z ‾ = x − i y , x , y ∈ R z = x + iy, \quad \overline{z} = x — iy, \quad x, y \in \mathbb{R}
Подставим в уравнение:
( x − i y ) + 1 = 1 ( x + i y ) + 1 = 1 x + 1 + i y (x — iy) + 1 = \frac{1}{(x + iy) + 1} = \frac{1}{x + 1 + iy}
Шаг 3. Избавление от дроби
Перепишем:
z ‾ + 1 = 1 z + 1 ⇒ ( z ‾ + 1 ) ( z + 1 ) = 1 \overline{z} + 1 = \frac{1}{z + 1} \quad \Rightarrow \quad (\overline{z} + 1)(z + 1) = 1
Это избавляет нас от дроби.
Шаг 4. Раскрытие скобок
( z ‾ + 1 ) ( z + 1 ) = z ‾ z + z ‾ + z + 1 (\overline{z} + 1)(z + 1) = \overline{z}z + \overline{z} + z + 1
Подставляем:
z ‾ z + z ‾ + z + 1 = 1 \overline{z}z + \overline{z} + z + 1 = 1
Шаг 5. Упрощение
z ‾ z + z ‾ + z + 1 = 1 ⇒ z ‾ z + z ‾ + z = 0 \overline{z}z + \overline{z} + z + 1 = 1 \Rightarrow \overline{z}z + \overline{z} + z = 0
Шаг 6. Подстановка z = x + i y z = x + iy z ‾ = x − i y \overline{z} = x — iy
Рассчитаем каждый член:
z ‾ z = ( x − i y ) ( x + i y ) = x 2 + y 2 \overline{z}z = (x — iy)(x + iy) = x^2 + y^2 z ‾ + z = ( x − i y ) + ( x + i y ) = 2 x \overline{z} + z = (x — iy) + (x + iy) = 2x Подставляем:
x 2 + y 2 + 2 x = 0 x^2 + y^2 + 2x = 0
Шаг 7. Преобразование уравнения
x 2 + 2 x + y 2 = 0 x^2 + 2x + y^2 = 0
Добавим и вычтем 1:
x 2 + 2 x + 1 + y 2 − 1 = 0 ⇒ ( x + 1 ) 2 + y 2 = 1 x^2 + 2x + 1 + y^2 — 1 = 0 \Rightarrow (x + 1)^2 + y^2 = 1
Шаг 8. Геометрическая интерпретация
Это уравнение окружности с центром в точке ( − 1 , 0 ) (-1, 0) R = 1 R = 1
( x + 1 ) 2 + y 2 = 1 ⇒ ( x − ( − 1 ) ) 2 + ( y − 0 ) 2 = 1 2 (x + 1)^2 + y^2 = 1 \quad \Rightarrow \quad (x — (-1))^2 + (y — 0)^2 = 1^2
Ответы на вопросы
а) Корень, у которого действительная часть наименьшая
Цель — найти z = x + i y z = x + iy x x
Поскольку центр окружности в точке ( − 1 , 0 ) (-1, 0) x x
x min = − 1 − 1 = − 2 , y = 0 x_{\min} = -1 — 1 = -2,\quad y = 0
Проверка:
( x + 1 ) 2 + y 2 = ( − 2 + 1 ) 2 + 0 2 = ( − 1 ) 2 + 0 = 1 (x + 1)^2 + y^2 = (-2 + 1)^2 + 0^2 = (-1)^2 + 0 = 1
То есть точка лежит на окружности.
Ответ:
z = − 2 z = -2
б) Корень, у которого мнимая часть наименьшая
Теперь минимизируем y y
Так как окружность имеет центр y = 0 y = 0
y min = − 1 , x = − 1 y_{\min} = -1, \quad x = -1
Проверка:
( − 1 + 1 ) 2 + ( − 1 ) 2 = 0 + 1 = 1 (-1 + 1)^2 + (-1)^2 = 0 + 1 = 1
Точка лежит на окружности.
Ответ:
z = − 1 − i z = -1 — i
в) Корень, который ближе всего расположен к началу координат
Ищем точку на окружности, ближайшую к 0 + 0 i 0 + 0i
∣ z ∣ = x 2 + y 2 |z| = \sqrt{x^2 + y^2}
Окружность: ( x + 1 ) 2 + y 2 = 1 (x + 1)^2 + y^2 = 1
Подставим x = 0 , y = 0 x = 0, y = 0
( 0 + 1 ) 2 + 0 2 = 1 ⇒ 1 + 0 = 1 (0 + 1)^2 + 0^2 = 1 \Rightarrow 1 + 0 = 1
Точка принадлежит окружности.
Рассчитаем расстояние:
∣ z ∣ = 0 2 + 0 2 = 0 ⇒ z = 0 |z| = \sqrt{0^2 + 0^2} = 0 \Rightarrow z = 0
Ответ:
z = 0 z = 0
г) Корень, который ближе всего расположен к числу i i
Точка i i ( 0 , 1 ) (0, 1)
Ищем точку на окружности, ближайшую к ( 0 , 1 ) (0, 1)
Метод: Минимизировать расстояние между точками окружности и точкой ( 0 , 1 ) (0,1)
Используем параметрическое уравнение окружности:
x = − 1 + cos θ , y = sin θ x = -1 + \cos\theta,\quad y = \sin\theta
Расстояние от z = x + i y z = x + iy i i
∣ z − i ∣ = x 2 + ( y − 1 ) 2 |z — i| = \sqrt{x^2 + (y — 1)^2}
Подставим параметры:
x = − 1 + cos θ x = -1 + \cos\theta y = sin θ y = \sin\theta ∣ z − i ∣ 2 = ( − 1 + cos θ ) 2 + ( sin θ − 1 ) 2 |z — i|^2 = (-1 + \cos\theta)^2 + (\sin\theta — 1)^2
Минимизируем. Наиболее близкое направление — прямая от центра окружности к i = ( 0 , 1 ) i = (0,1)
Вектор от центра ( − 1 , 0 ) (-1, 0) ( 0 , 1 ) (0, 1)
v ⃗ = ( 1 , 1 ) , ∣ v ⃗ ∣ = 2 ⇒ единичный вектор: ( 1 2 , 1 2 ) \vec{v} = (1, 1),\quad |\vec{v}| = \sqrt{2} \Rightarrow \text{единичный вектор: } \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)
Координаты ближайшей точки:
x = − 1 + 1 2 , y = 0 + 1 2 = 1 2 x = -1 + \frac{1}{\sqrt{2}},\quad y = 0 + \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}}
Или:
x = 1 − 2 2 , y = 1 2 x = \frac{1 — \sqrt{2}}{\sqrt{2}},\quad y = \frac{1}{\sqrt{2}}
Ответ:
z = 1 − 2 + i 2 z = \frac{1 — \sqrt{2} + i}{\sqrt{2}}
Итоговые ответы:
а)
z = − 2 \boxed{z = -2}
б)
z = − 1 − i \boxed{z = -1 — i}
в)
z = 0 \boxed{z = 0}
г)
z = 1 − 2 + i 2 \boxed{z = \frac{1 — \sqrt{2} + i}{\sqrt{2}}}