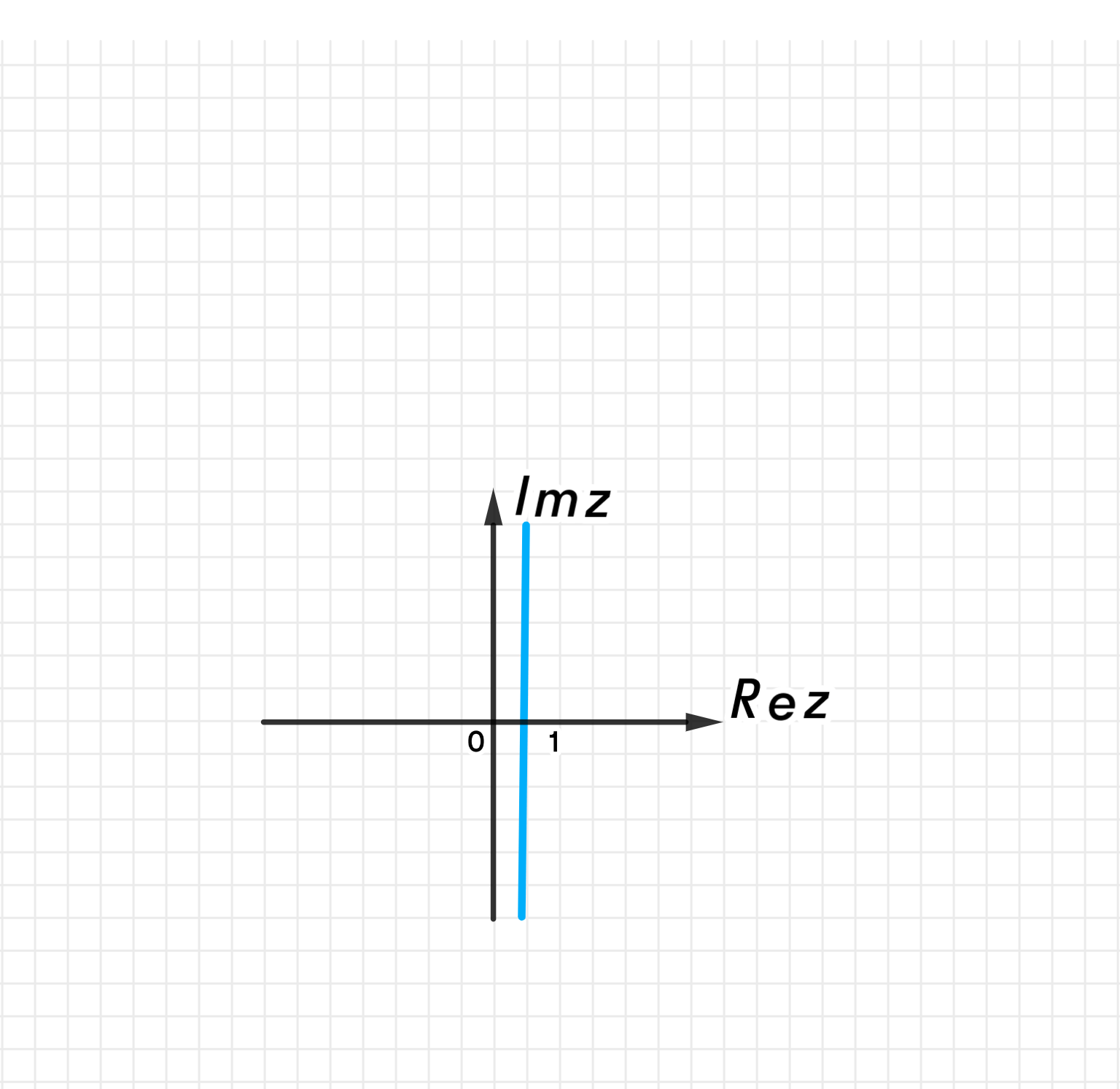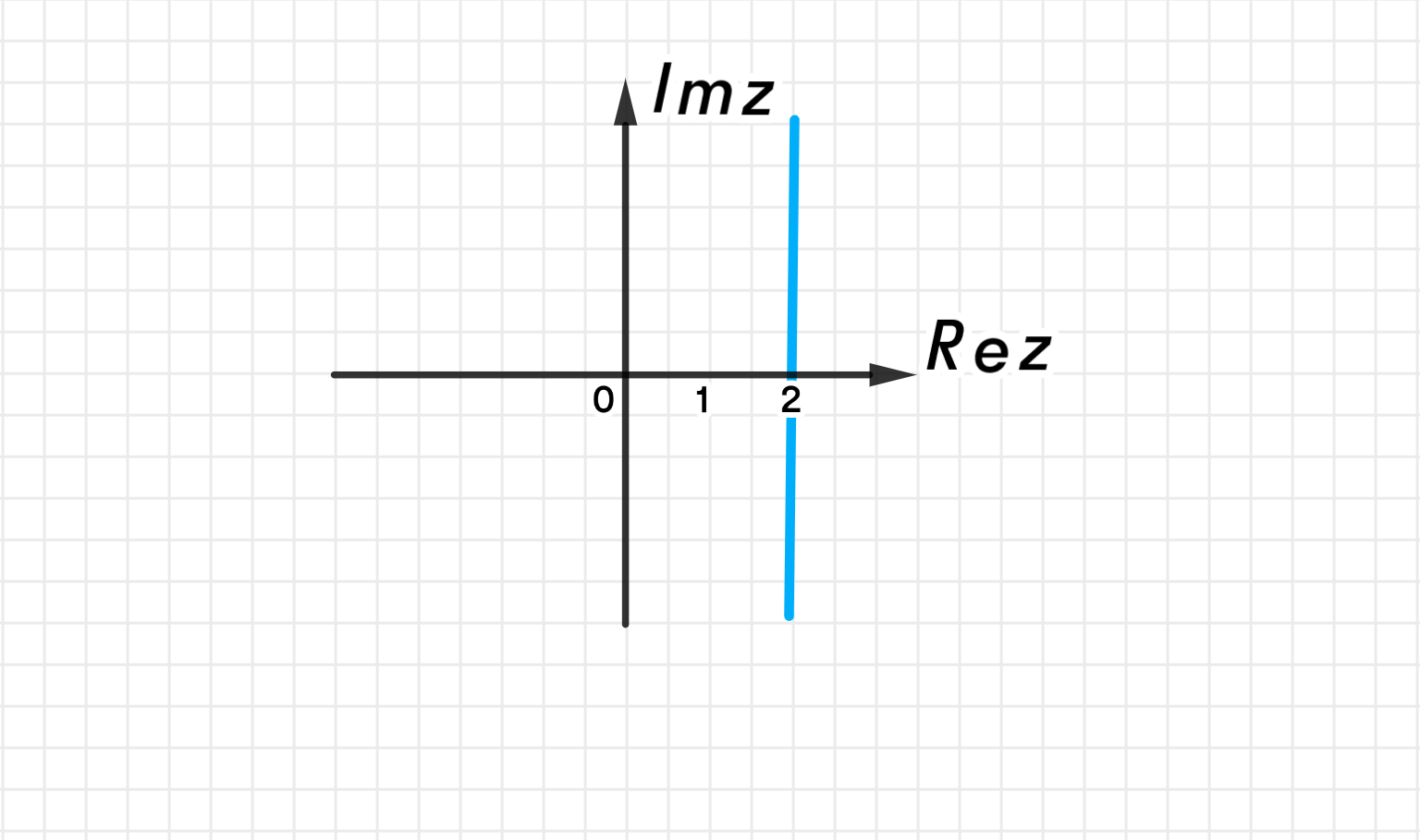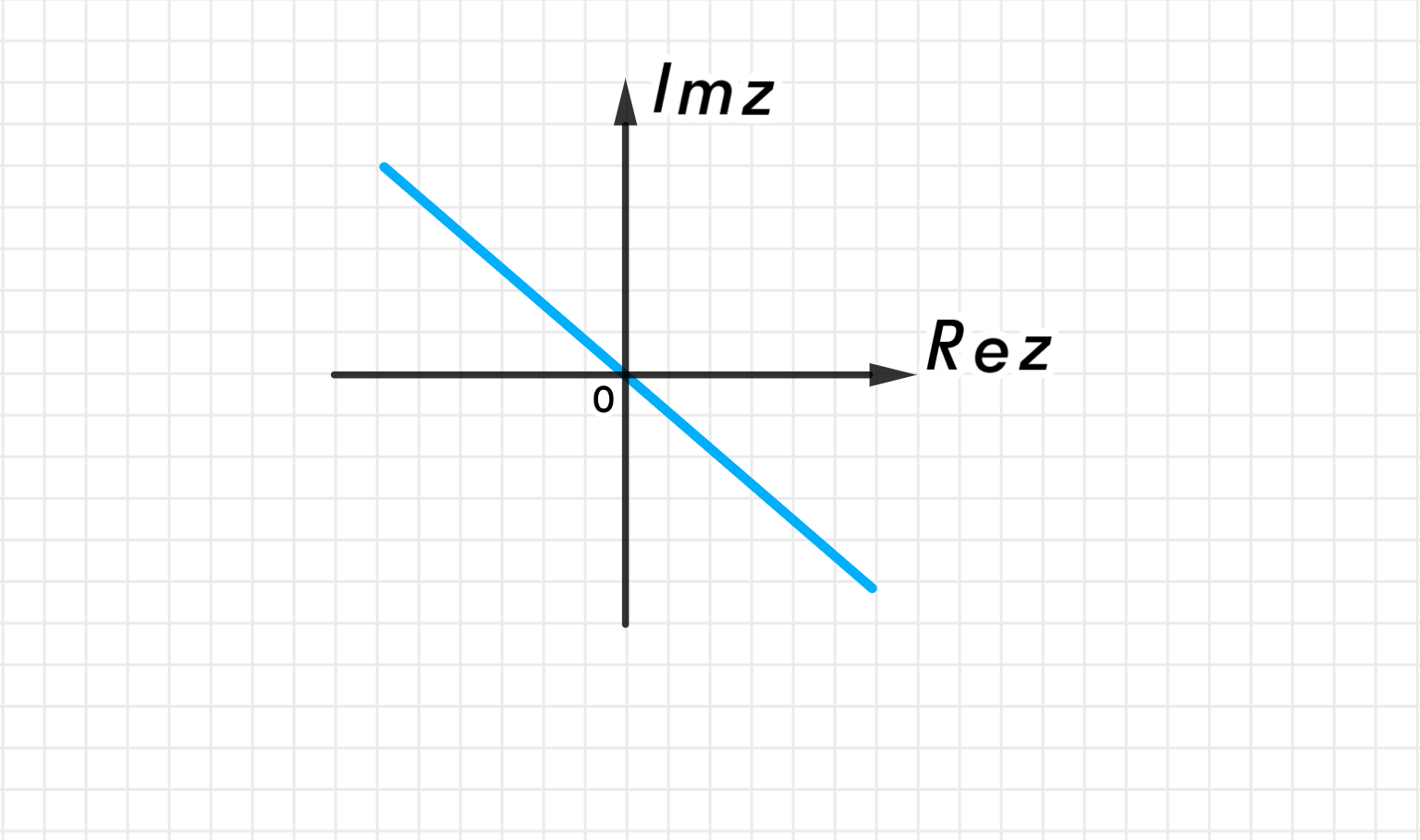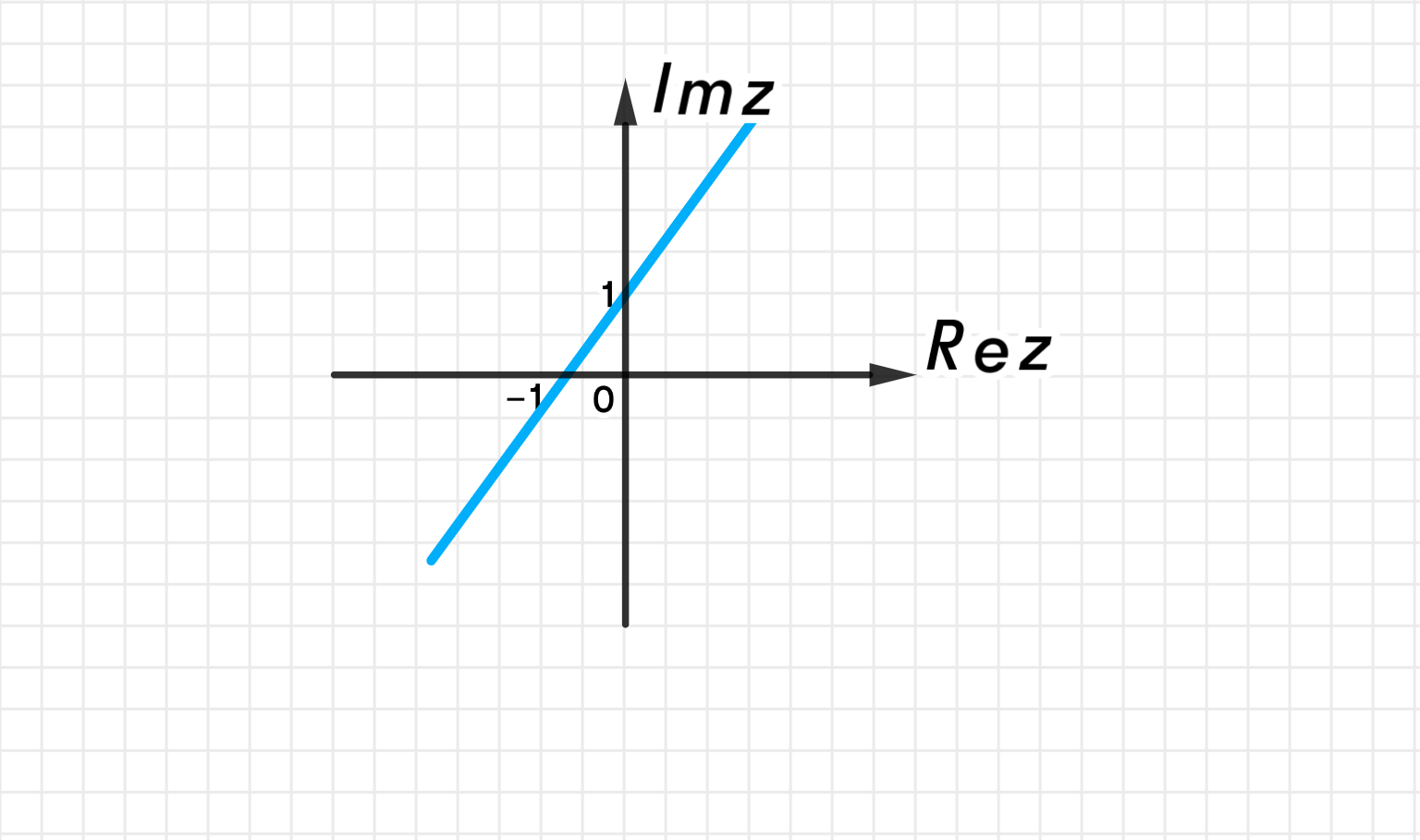ГДЗ Мордкович 10 Класс Профильный Уровень по Алгебре Задачник 📕 — Все Части

Алгебра Профильный Уровень

10 класс задачник профильный уровень Мордкович

10 класс

Тип

ГДЗ, Решебник.

Автор

А.Г. Мордкович, П. В. Семенов.

Год

2015-2020.

Издательство

Мнемозина.

Описание

Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.

ГДЗ по Алгебре 10 Класс Номер 34.10 Профильный Уровень Мордкович — Подробные Ответы

Задача

Изобразите на комплексной плоскости множество всех чисел z, удовлетворяющих уравнению:

а) $∣ z ∣ = ∣ z - 1 ∣$ ;

б) $∣ z - 1 ∣ = ∣ z - 3 ∣$ ;

в) $∣ z - 1 ∣ = ∣ z - i ∣$ ;

г) $∣ z + 3 i ∣ = ∣ z + 4 ∣$

Краткий ответ:

Изобразить на комплексной плоскости множество всех чисел $z$ , удовлетворяющих уравнению:

а) $∣ z ∣ = ∣ z - 1 ∣$ ;
$∣ x + y i ∣ = ∣ x + y i - 1 ∣;$
$\sqrt{x^{2} + y^{2}} = \sqrt{(x - 1)^{2} + y^{2}};$
$x^{2} + y^{2} = (x - 1)^{2} + y^{2};$
$x^{2} = x^{2} - 2 x + 1;$
$- 2 x + 1 = 0;$
$2 x = 1;$
$x = 0.5;$

б) $∣ z - 1 ∣ = ∣ z - 3 ∣$ ;
$∣ x + y i - 1 ∣ = ∣ x + y i - 3 ∣;$
$\sqrt{(x - 1)^{2} + y^{2}} = \sqrt{(x - 3)^{2} + y^{2}};$
$(x - 1)^{2} + y^{2} = (x - 3)^{2} + y^{2};$
$x^{2} - 2 x + 1 = x^{2} - 6 x + 9;$
$4 x = 8;$
$x = 2;$

в) $∣ z - 1 ∣ = ∣ z - i ∣$ ;
$∣ x + y i - 1 ∣ = ∣ x + y i - i ∣;$
$\sqrt{(x - 1)^{2} + y^{2}} = \sqrt{x^{2} + (y - 1)^{2}};$
$(x - 1)^{2} + y^{2} = x^{2} + (y - 1)^{2};$
$x^{2} - 2 x + 1 + y^{2} = x^{2} + y^{2} - 2 y + 1;$
$- 2 x = - 2 y;$
$y = x;$

г) $∣ z + 3 i ∣ = ∣ z + 4 ∣$ ;
$∣ x + y i + 3 i ∣ = ∣ x + y i + 4 ∣;$
$\sqrt{x^{2} + (y + 3)^{2}} = \sqrt{(x + 4)^{2} + y^{2}};$
$x^{2} + (y + 3)^{2} = (x + 4)^{2} + y^{2};$
$x^{2} + y^{2} + 6 y + 9 = x^{2} + 8 x + 16 + y^{2};$
$6 y = 7 + 8 x;$
$y = \frac{7}{6} + \frac{4}{3} x;$

Подробный ответ:

а) $∣ z ∣ = ∣ z - 1 ∣$

Шаг 1: Представим $z$ в виде $z = x + y i$

Тогда $∣ z ∣ = \sqrt{x^{2} + y^{2}}$
$z - 1 = x - 1 + y i \Rightarrow ∣ z - 1 ∣ = \sqrt{(x - 1)^{2} + y^{2}}$

Шаг 2: Приравниваем модули

$\sqrt{x^{2} + y^{2}} = \sqrt{(x - 1)^{2} + y^{2}}$

Шаг 3: Возводим обе части в квадрат

$x^{2} + y^{2} = (x - 1)^{2} + y^{2}$

Шаг 4: Упростим

$x^{2} + y^{2} = x^{2} - 2 x + 1 + y^{2}$

Вычитаем $x^{2} + y^{2}$ с обеих сторон:

$0 = - 2 x + 1 \Rightarrow 2 x = 1 \Rightarrow x = 0.5$

Ответ (а):

Это прямая $x = \frac{1}{2}$ .
На комплексной плоскости — множество всех точек, находящихся на равном расстоянии от начала координат и точки $1 + 0 i$ .
Это — геометрическое место точек, равноудалённых от двух фиксированных точек, что и даёт перпендикулярную биссектрису отрезка $[0, 1]$ на действительной оси.

б) $∣ z - 1 ∣ = ∣ z - 3 ∣$

Шаг 1: Пусть $z = x + y i$

$z - 1 = x - 1 + y i \Rightarrow ∣ z - 1 ∣ = \sqrt{(x - 1)^{2} + y^{2}}$
$z - 3 = x - 3 + y i \Rightarrow ∣ z - 3 ∣ = \sqrt{(x - 3)^{2} + y^{2}}$

Шаг 2: Приравниваем модули и возводим в квадрат

$(x - 1)^{2} + y^{2} = (x - 3)^{2} + y^{2}$

Убираем $y^{2}$ с обеих сторон:

$(x - 1)^{2} = (x - 3)^{2}$

Шаг 3: Раскроем скобки

$x^{2} - 2 x + 1 = x^{2} - 6 x + 9$

Упростим:

$- 2 x + 1 = - 6 x + 9 \Rightarrow 4 x = 8 \Rightarrow x = 2$

Ответ (б):

Это прямая $x = 2$ — множество точек, равноудалённых от двух точек $1$ и $3$ на вещественной оси.
Это — биссектриса отрезка между точками $1 + 0 i$ и $3 + 0 i$ .

в) $∣ z - 1 ∣ = ∣ z - i ∣$

Шаг 1: $z = x + y i$

$z - 1 = x - 1 + y i \Rightarrow ∣ z - 1 ∣ = \sqrt{(x - 1)^{2} + y^{2}}$
$z - i = x + (y - 1) i \Rightarrow ∣ z - i ∣ = \sqrt{x^{2} + (y - 1)^{2}}$

Шаг 2: Приравниваем и возводим в квадрат

$(x - 1)^{2} + y^{2} = x^{2} + (y - 1)^{2}$

Шаг 3: Раскрываем скобки

Левая часть:

$x^{2} - 2 x + 1 + y^{2}$

Правая часть:

$x^{2} + y^{2} - 2 y + 1$

Сравним:

$x^{2} - 2 x + 1 + y^{2} = x^{2} + y^{2} - 2 y + 1$

Убираем $x^{2}, y^{2}, 1$ с обеих сторон:

$- 2 x = - 2 y \Rightarrow x = y$

Ответ (в):

Это прямая $y = x$ .
Множество точек, равноудалённых от точек $1 + 0 i$ и $0 + i$ , лежит на биссектрисе угла между горизонтальной и вертикальной прямыми, проходящей через начало координат.

г) $∣ z + 3 i ∣ = ∣ z + 4 ∣$

Шаг 1: $z = x + y i$

$z + 3 i = x + (y + 3) i \Rightarrow ∣ z + 3 i ∣ = \sqrt{x^{2} + (y + 3)^{2}}$
$z + 4 = (x + 4) + y i \Rightarrow ∣ z + 4 ∣ = \sqrt{(x + 4)^{2} + y^{2}}$

Шаг 2: Приравниваем модули и возводим в квадрат

$x^{2} + (y + 3)^{2} = (x + 4)^{2} + y^{2}$

Шаг 3: Раскрываем скобки

Левая часть:

$x^{2} + y^{2} + 6 y + 9$

Правая часть:

$x^{2} + 8 x + 16 + y^{2}$

Сравним:

$x^{2} + y^{2} + 6 y + 9 = x^{2} + 8 x + 16 + y^{2}$

Убираем $x^{2} + y^{2}$ с обеих сторон:

$6 y + 9 = 8 x + 16$

Шаг 4: Выразим $y$ через $x$

$6 y = 8 x + 7 \Rightarrow y = \frac{8 x + 7}{6} = \frac{4}{3} x + \frac{7}{6}$

Ответ (г):

Это прямая, заданная уравнением:

$y = \frac{4}{3} x + \frac{7}{6}$

Геометрически: множество точек, равноудалённых от $z = - 3 i$ и $z = - 4$ , т.е. от точек $(0, - 3)$ и $(- 4, 0)$ .

Оцени решение