Подробный ответ:
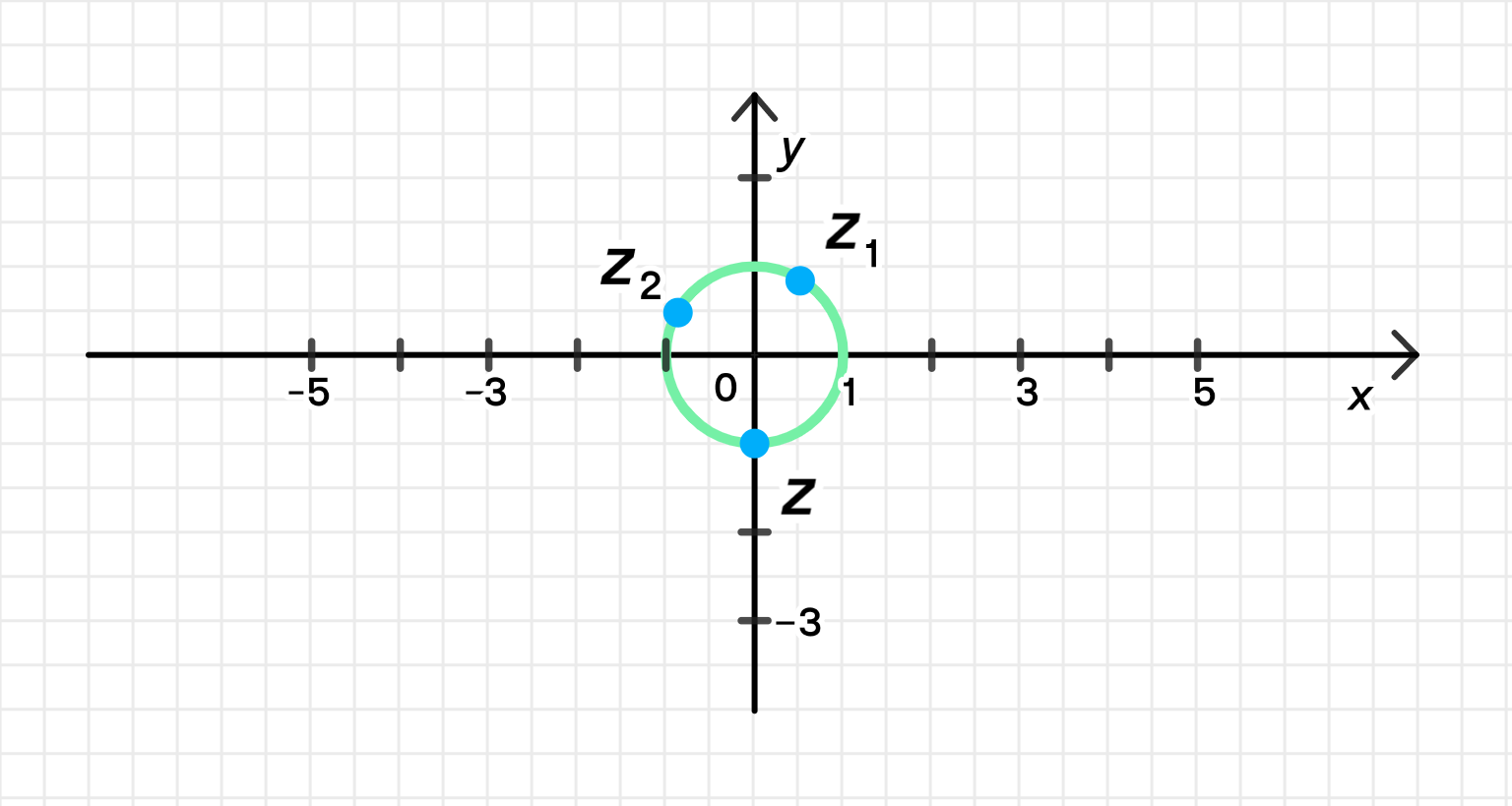
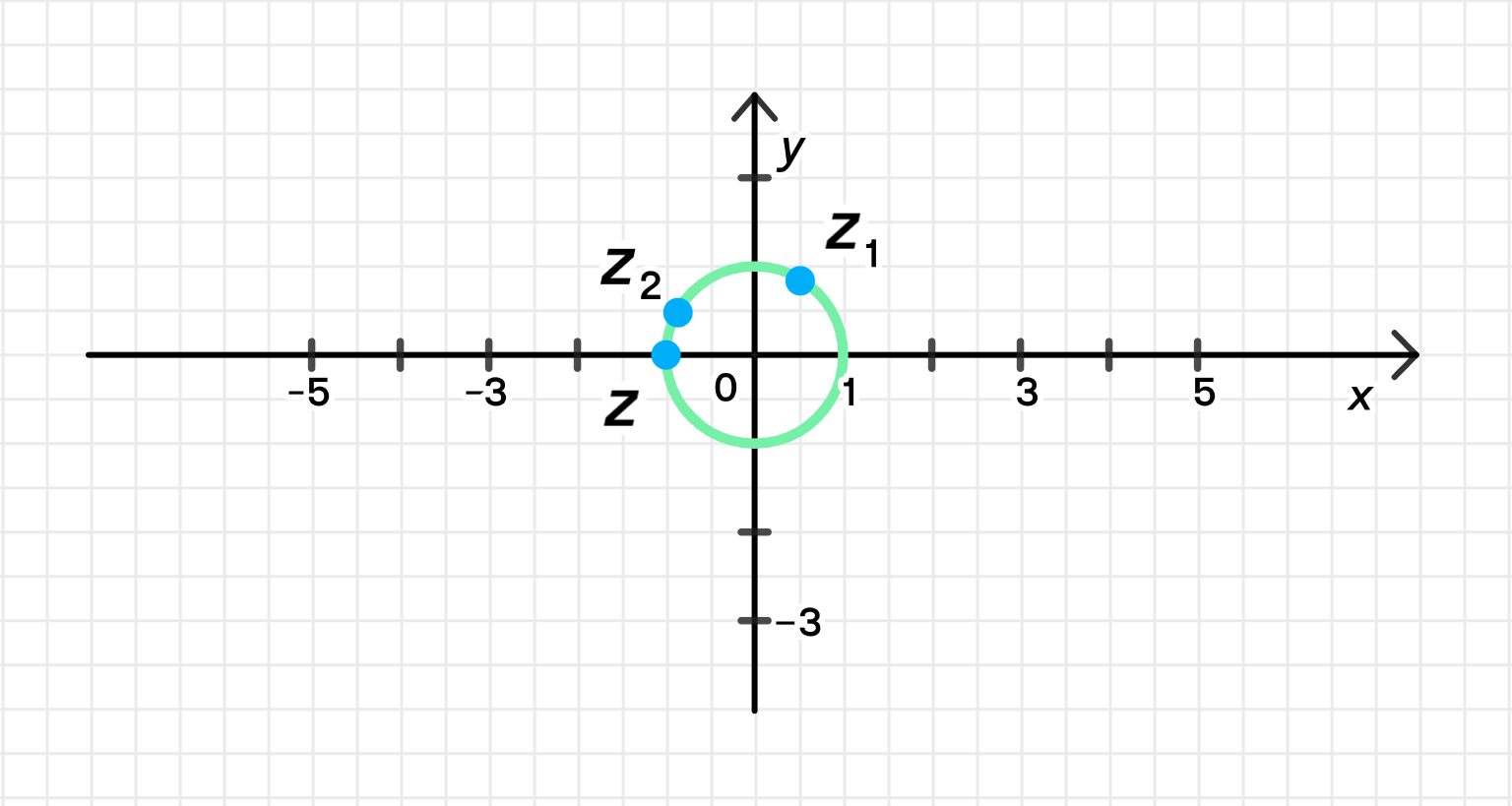
Даны комплексные числа:
z 1 = 1 2 + 3 2 i = cos π 3 + i sin π 3 ; z_1 = \frac{1}{2} + \frac{\sqrt{3}}{2}i = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3}; z 2 = − 3 2 + 1 2 i = cos 5 π 6 + i sin 5 π 6 . z_2 = -\frac{\sqrt{3}}{2} + \frac{1}{2}i = \cos \frac{5\pi}{6} + i \sin \frac{5\pi}{6}.
Давайте разберем каждый пункт задачи подробно.
а) Найти z = z 1 z 2 z = \frac{z_1}{z_2}
Для вычисления частного двух комплексных чисел в полярной форме используем следующее правило:
z 1 z 2 = r 1 r 2 ⋅ ( cos ( θ 1 − θ 2 ) + i sin ( θ 1 − θ 2 ) ) , \frac{z_1}{z_2} = \frac{r_1}{r_2} \cdot \left( \cos(\theta_1 — \theta_2) + i \sin(\theta_1 — \theta_2) \right),
где r 1 , r 2 r_1, r_2 z 1 z_1 z 2 z_2 θ 1 , θ 2 \theta_1, \theta_2
Модуль z 1 z_1
∣ z 1 ∣ = ( 1 2 ) 2 + ( 3 2 ) 2 = 1 4 + 3 4 = 1 = 1. |z_1| = \sqrt{\left( \frac{1}{2} \right)^2 + \left( \frac{\sqrt{3}}{2} \right)^2} = \sqrt{\frac{1}{4} + \frac{3}{4}} = \sqrt{1} = 1.
Таким образом, r 1 = 1 r_1 = 1
Модуль z 2 z_2
∣ z 2 ∣ = ( − 3 2 ) 2 + ( 1 2 ) 2 = 3 4 + 1 4 = 1 = 1. |z_2| = \sqrt{\left( -\frac{\sqrt{3}}{2} \right)^2 + \left( \frac{1}{2} \right)^2} = \sqrt{\frac{3}{4} + \frac{1}{4}} = \sqrt{1} = 1.
Таким образом, r 2 = 1 r_2 = 1
Аргумент z 1 z_1 π 3 \frac{\pi}{3} z 1 = cos π 3 + i sin π 3 z_1 = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3}
Аргумент z 2 z_2 5 π 6 \frac{5\pi}{6} z 2 = cos 5 π 6 + i sin 5 π 6 z_2 = \cos \frac{5\pi}{6} + i \sin \frac{5\pi}{6}
Теперь можем найти z = z 1 z 2 z = \frac{z_1}{z_2}
z = 1 1 ⋅ ( cos ( π 3 − 5 π 6 ) + i sin ( π 3 − 5 π 6 ) ) . z = \frac{1}{1} \cdot \left( \cos \left( \frac{\pi}{3} — \frac{5\pi}{6} \right) + i \sin \left( \frac{\pi}{3} — \frac{5\pi}{6} \right) \right).
Вычитаем углы:
π 3 − 5 π 6 = 2 π 6 − 5 π 6 = − 3 π 6 = − π 2 . \frac{\pi}{3} — \frac{5\pi}{6} = \frac{2\pi}{6} — \frac{5\pi}{6} = -\frac{3\pi}{6} = -\frac{\pi}{2}.
Таким образом, выражение для z z
z = cos ( − π 2 ) + i sin ( − π 2 ) . z = \cos \left( -\frac{\pi}{2} \right) + i \sin \left( -\frac{\pi}{2} \right).
Известно, что:
cos ( − π 2 ) = 0 , sin ( − π 2 ) = − 1. \cos \left( -\frac{\pi}{2} \right) = 0, \quad \sin \left( -\frac{\pi}{2} \right) = -1.
Следовательно:
z = 0 − i ⋅ 1 = − i . z = 0 — i \cdot 1 = -i.
Ответ: arg z = − π 2 \arg z = -\frac{\pi}{2}
б) Найти z = z 1 3 z = z_1^3
Для возведения комплексного числа в степень в полярной форме используется формула:
z 1 n = r 1 n ⋅ ( cos ( n θ 1 ) + i sin ( n θ 1 ) ) , z_1^n = r_1^n \cdot \left( \cos(n \theta_1) + i \sin(n \theta_1) \right),
где r 1 r_1 z 1 z_1 θ 1 \theta_1 z 1 z_1 n n
Модуль z 1 = 1 z_1 = 1 r 1 3 = 1 3 = 1 r_1^3 = 1^3 = 1
Аргумент z 1 = π 3 z_1 = \frac{\pi}{3} n θ 1 = 3 ⋅ π 3 = π n \theta_1 = 3 \cdot \frac{\pi}{3} = \pi
Теперь вычислим z 1 3 z_1^3
z 1 3 = 1 ⋅ ( cos π + i sin π ) = cos π + i sin π . z_1^3 = 1 \cdot \left( \cos \pi + i \sin \pi \right) = \cos \pi + i \sin \pi.
Известно, что:
cos π = − 1 , sin π = 0. \cos \pi = -1, \quad \sin \pi = 0.
Следовательно:
z 1 3 = − 1 + i ⋅ 0 = − 1. z_1^3 = -1 + i \cdot 0 = -1.
Ответ: arg z = π \arg z = \pi
в) Найти z = z 1 4 z 2 3 z = \frac{z_1^4}{z_2^3}
Для деления степеней комплексных чисел в полярной форме используем то же правило, что и для деления двух комплексных чисел. Для этого нужно найти:
z = z 1 4 z 2 3 = r 1 4 r 2 3 ⋅ ( cos ( θ 1 ⋅ 4 − θ 2 ⋅ 3 ) + i sin ( θ 1 ⋅ 4 − θ 2 ⋅ 3 ) ) . z = \frac{z_1^4}{z_2^3} = \frac{r_1^4}{r_2^3} \cdot \left( \cos(\theta_1 \cdot 4 — \theta_2 \cdot 3) + i \sin(\theta_1 \cdot 4 — \theta_2 \cdot 3) \right).
Модуль z 1 4 = r 1 4 = 1 4 = 1 z_1^4 = r_1^4 = 1^4 = 1
Модуль z 2 3 = r 2 3 = 1 3 = 1 z_2^3 = r_2^3 = 1^3 = 1
Таким образом, модуль для z z 1 1
Теперь вычислим аргумент:
θ 1 ⋅ 4 = 4 ⋅ π 3 = 4 π 3 , \theta_1 \cdot 4 = 4 \cdot \frac{\pi}{3} = \frac{4\pi}{3}, θ 2 ⋅ 3 = 3 ⋅ 5 π 6 = 15 π 6 = 5 π 2 . \theta_2 \cdot 3 = 3 \cdot \frac{5\pi}{6} = \frac{15\pi}{6} = \frac{5\pi}{2}.
Вычитаем аргументы:
4 π 3 − 5 π 2 = 8 π 6 − 15 π 6 = − 7 π 6 . \frac{4\pi}{3} — \frac{5\pi}{2} = \frac{8\pi}{6} — \frac{15\pi}{6} = -\frac{7\pi}{6}.
Теперь подставляем это значение в формулу:
z = cos ( − 7 π 6 ) + i sin ( − 7 π 6 ) . z = \cos \left( -\frac{7\pi}{6} \right) + i \sin \left( -\frac{7\pi}{6} \right).
Известно, что:
cos ( − 7 π 6 ) = cos 5 π 6 , sin ( − 7 π 6 ) = sin 5 π 6 . \cos \left( -\frac{7\pi}{6} \right) = \cos \frac{5\pi}{6}, \quad \sin \left( -\frac{7\pi}{6} \right) = \sin \frac{5\pi}{6}.
Следовательно:
z = cos 5 π 6 + i sin 5 π 6 . z = \cos \frac{5\pi}{6} + i \sin \frac{5\pi}{6}.
Ответ: arg z = 5 π 6 \arg z = \frac{5\pi}{6}
г) Найти z = z 1 31 z 2 33 z = \frac{z_1^{31}}{z_2^{33}}
Аналогично предыдущим пунктам, для деления степеней комплексных чисел в полярной форме:
z = z 1 31 z 2 33 = r 1 31 r 2 33 ⋅ ( cos ( θ 1 ⋅ 31 − θ 2 ⋅ 33 ) + i sin ( θ 1 ⋅ 31 − θ 2 ⋅ 33 ) ) . z = \frac{z_1^{31}}{z_2^{33}} = \frac{r_1^{31}}{r_2^{33}} \cdot \left( \cos(\theta_1 \cdot 31 — \theta_2 \cdot 33) + i \sin(\theta_1 \cdot 31 — \theta_2 \cdot 33) \right).
Модуль z 1 31 = r 1 31 = 1 31 = 1 z_1^{31} = r_1^{31} = 1^{31} = 1
Модуль z 2 33 = r 2 33 = 1 33 = 1 z_2^{33} = r_2^{33} = 1^{33} = 1
Таким образом, модуль для z z 1 1
Теперь вычислим аргумент:
θ 1 ⋅ 31 = 31 ⋅ π 3 = 31 π 3 , \theta_1 \cdot 31 = 31 \cdot \frac{\pi}{3} = \frac{31\pi}{3}, θ 2 ⋅ 33 = 33 ⋅ 5 π 6 = 165 π 6 = 55 π 2 . \theta_2 \cdot 33 = 33 \cdot \frac{5\pi}{6} = \frac{165\pi}{6} = \frac{55\pi}{2}.
Вычитаем аргументы:
31 π 3 − 55 π 2 = 62 π 6 − 165 π 6 = − 103 π 6 . \frac{31\pi}{3} — \frac{55\pi}{2} = \frac{62\pi}{6} — \frac{165\pi}{6} = -\frac{103\pi}{6}.
Для упрощения этого угла, добавим 2 π 2\pi 0 ≤ θ < 2 π 0 \leq \theta < 2\pi
− 103 π 6 + 2 π = − 103 π 6 + 12 π 6 = − 91 π 6 . -\frac{103\pi}{6} + 2\pi = -\frac{103\pi}{6} + \frac{12\pi}{6} = -\frac{91\pi}{6}.
Дополним угол до интервала [ 0 , 2 π ) [0, 2\pi)
− 91 π 6 + 2 π = − 91 π 6 + 12 π 6 = − 79 π 6 . -\frac{91\pi}{6} + 2\pi = -\frac{91\pi}{6} + \frac{12\pi}{6} = -\frac{79\pi}{6}.
Ответ: arg z = 5 π 6 \arg z = \frac{5\pi}{6}