Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 34.39 Профильный Уровень Мордкович — Подробные Ответы
Зная, что , , , изобразите на комплексной плоскости треугольник с вершинами , , , если:
а) ;
б) ;
в) ;
г) .
Даны комплексные числа:
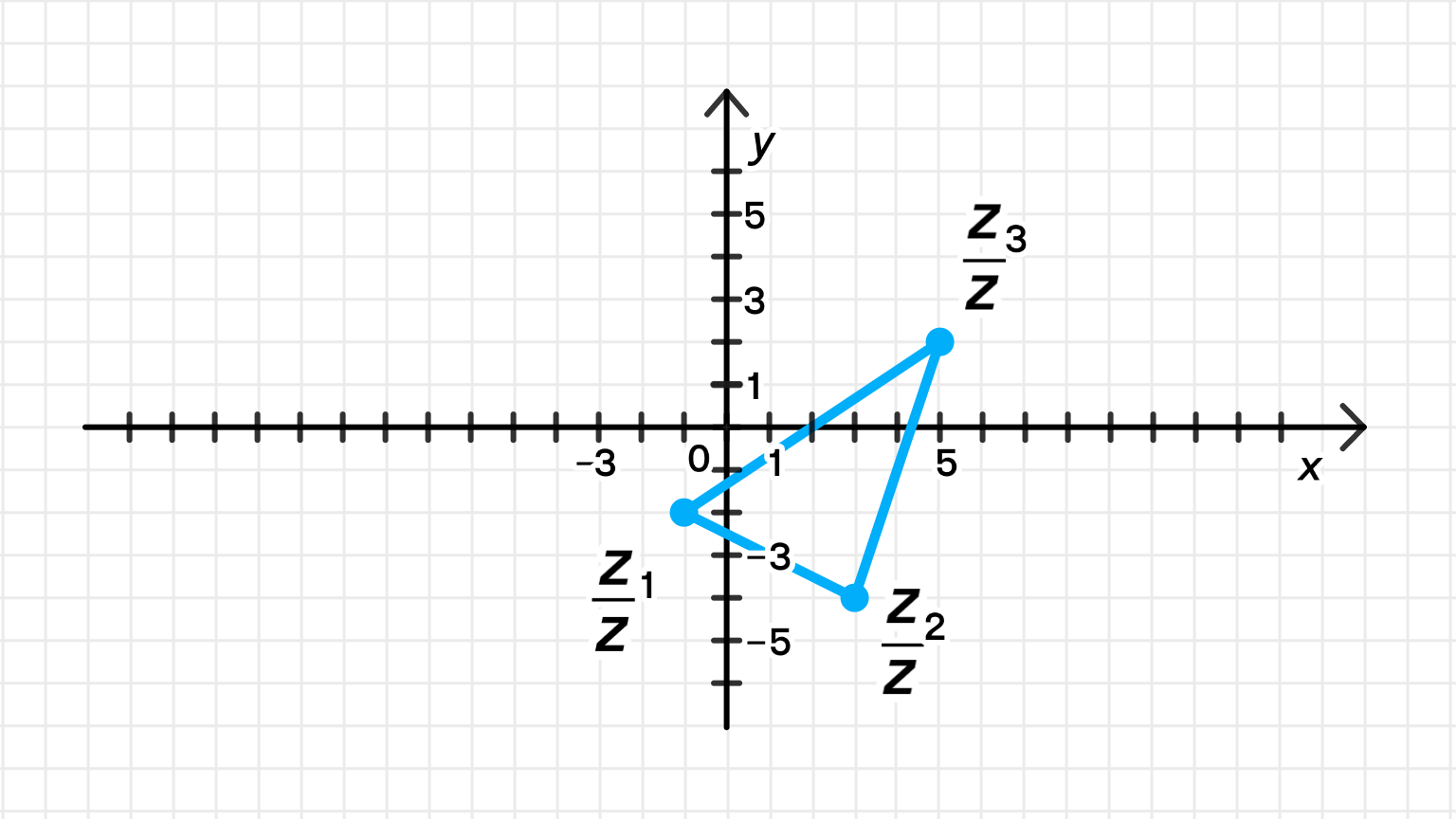
а) Если , тогда:
Треугольник с вершинами в точках .
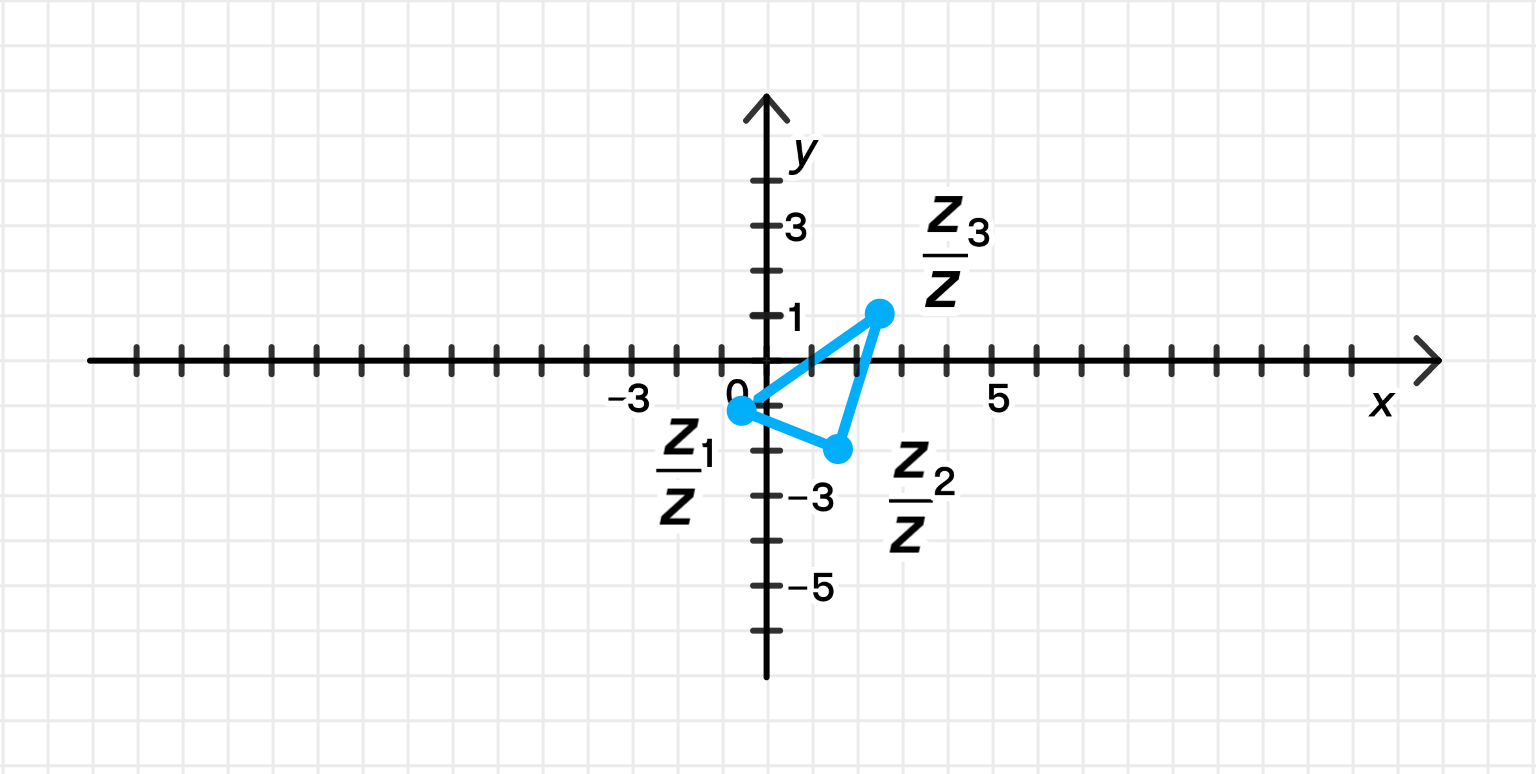
б) Если , тогда:
Треугольник с вершинами в точках .
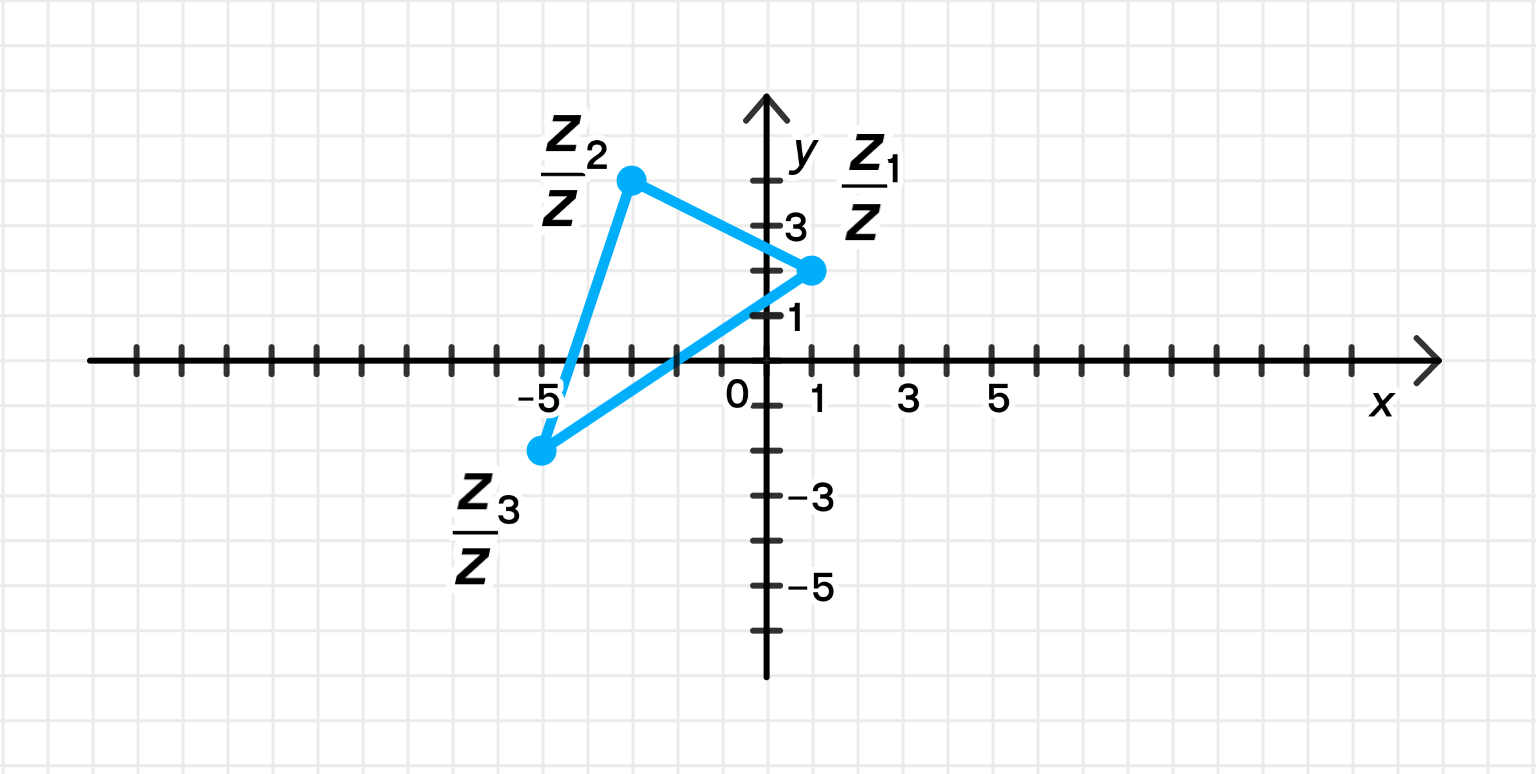
в) Если , тогда:
Треугольник с вершинами в точках .
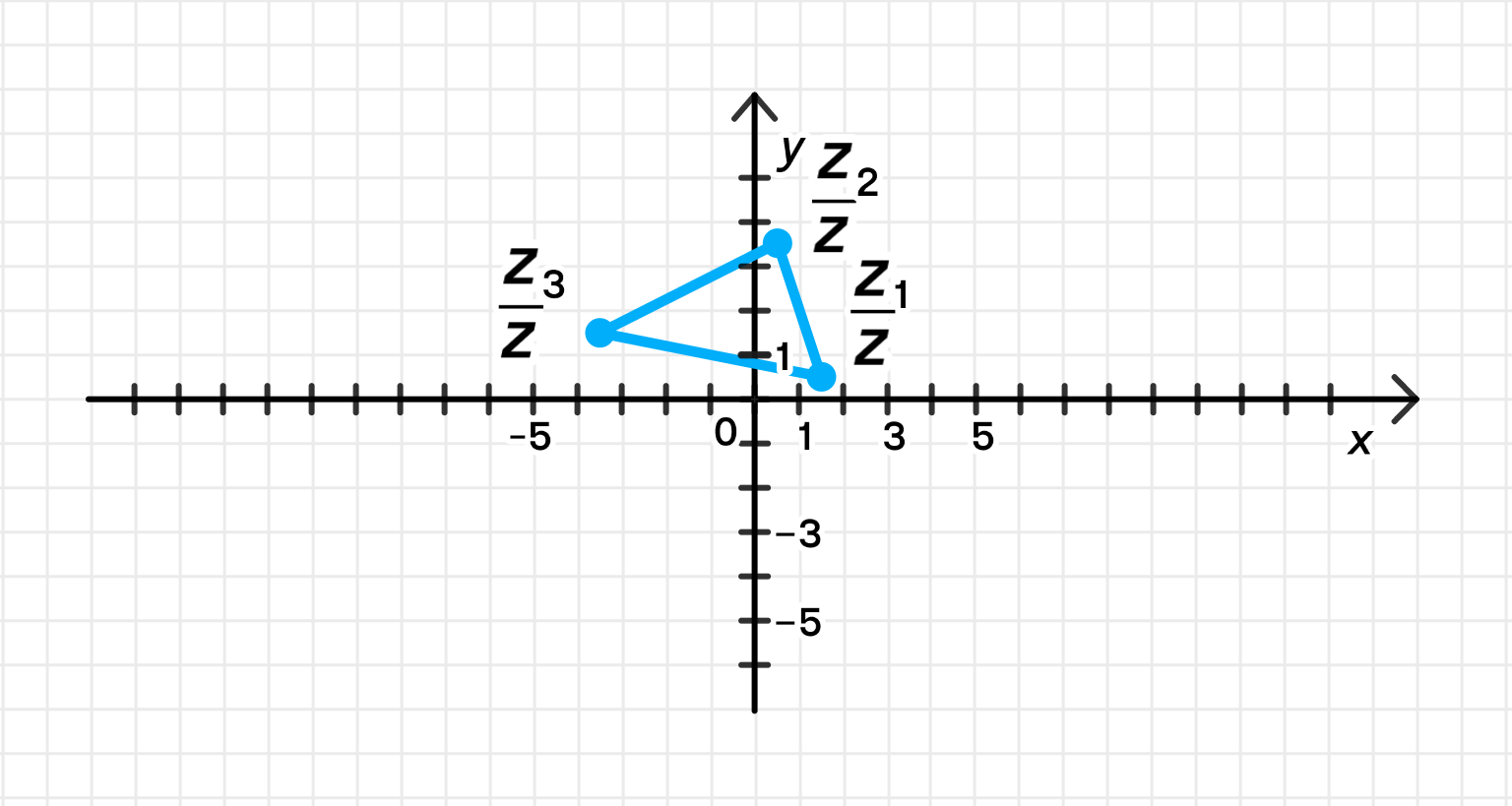
г) Если , тогда:
Треугольник с вершинами в точках .
Даны комплексные числа:
Нужно выполнить операции деления каждого из этих чисел на различные значения и для каждого случая построить треугольник с вершинами в точках .
Рассмотрим все возможные случаи для .
а) Если :
Нам нужно вычислить , где .
1. Перемножение :
Чтобы разделить комплексное число на , умножим и числитель, и знаменатель на сопряженное число , чтобы избавиться от мнимой части в знаменателе. В данном случае умножим числитель и знаменатель на :
Теперь подставим :
Результат:
2. Перемножение :
Точно так же умножим числитель и знаменатель на :
Так как :
Результат:
3. Перемножение :
Снова умножим числитель и знаменатель на :
Так как :
Результат:
Таким образом, для получаем:
Треугольник с вершинами в точках .
б) Если :
Теперь делим на .
1. Перемножение :
Чтобы разделить на , умножим числитель и знаменатель на :
Подставим :
Результат:
2. Перемножение :
Умножим числитель и знаменатель на :
Подставим :
Результат:
3. Перемножение :
Умножим числитель и знаменатель на :
Подставим :
Результат:
Таким образом, для получаем:
Треугольник с вершинами в точках .
в) Если :
Теперь делим на .
1. Перемножение :
Чтобы разделить на , умножим числитель и знаменатель на :
Подставим :
Результат:
2. Перемножение :
Умножим числитель и знаменатель на :
Подставим :
Результат:
3. Перемножение :
Умножим числитель и знаменатель на :
Подставим :
Результат:
Таким образом, для получаем:
Треугольник с вершинами в точках .
г) Если :
Наконец, делим на .
1. Перемножение :
В этом случае используем формулу для деления комплексных чисел. Умножим числитель и знаменатель на сопряженное число :
Результат:
2. Перемножение :
Умножим числитель и знаменатель на :
Результат:
3. Перемножение :
Умножим числитель и знаменатель на :
Результат:
Таким образом, для получаем:
Треугольник с вершинами в точках .