Задача
Воспользовавшись определением, найдите производную функции в точке x 0 x_0
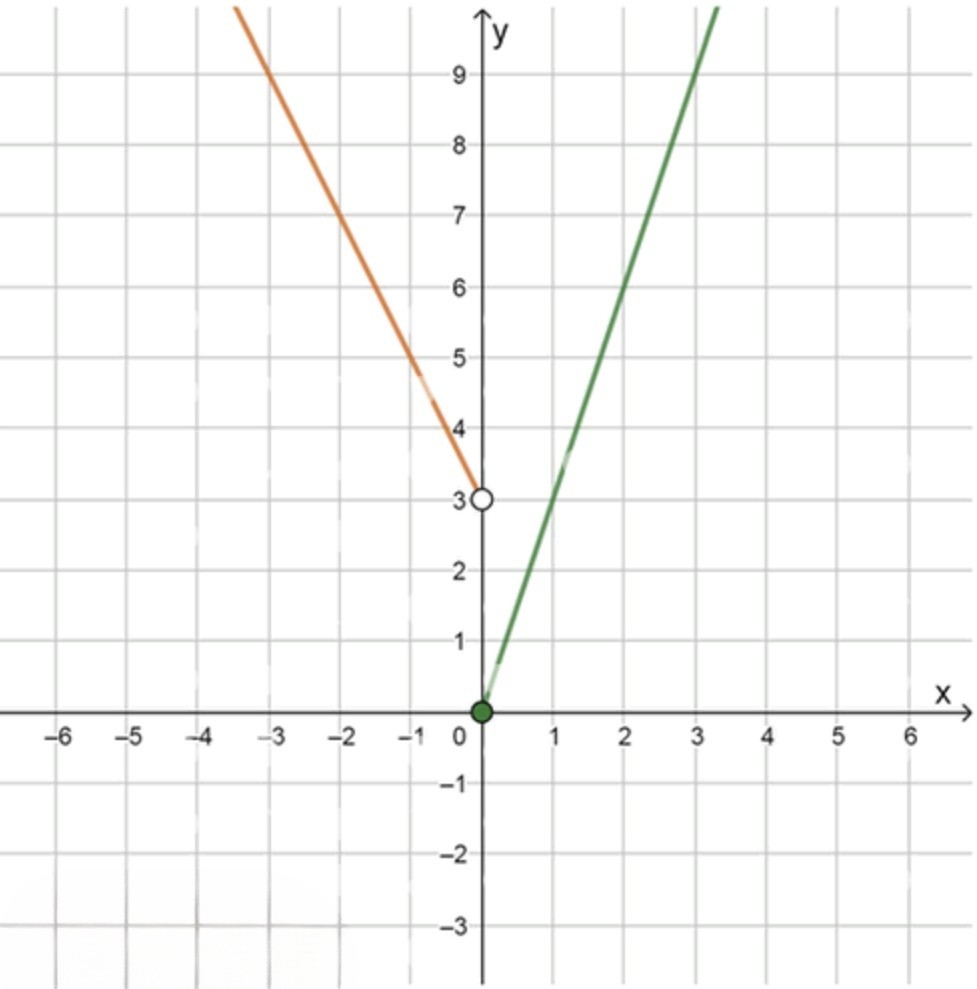
а)y = { 3 x , если x ⩾ 0 , − 2 x + 3 , если x < 0 ; x 0 = 0. y = \begin{cases} 3x, & \text{если } x \geqslant 0, \\ -2x + 3, & \text{если } x < 0; \end{cases} \quad x_0 = 0.
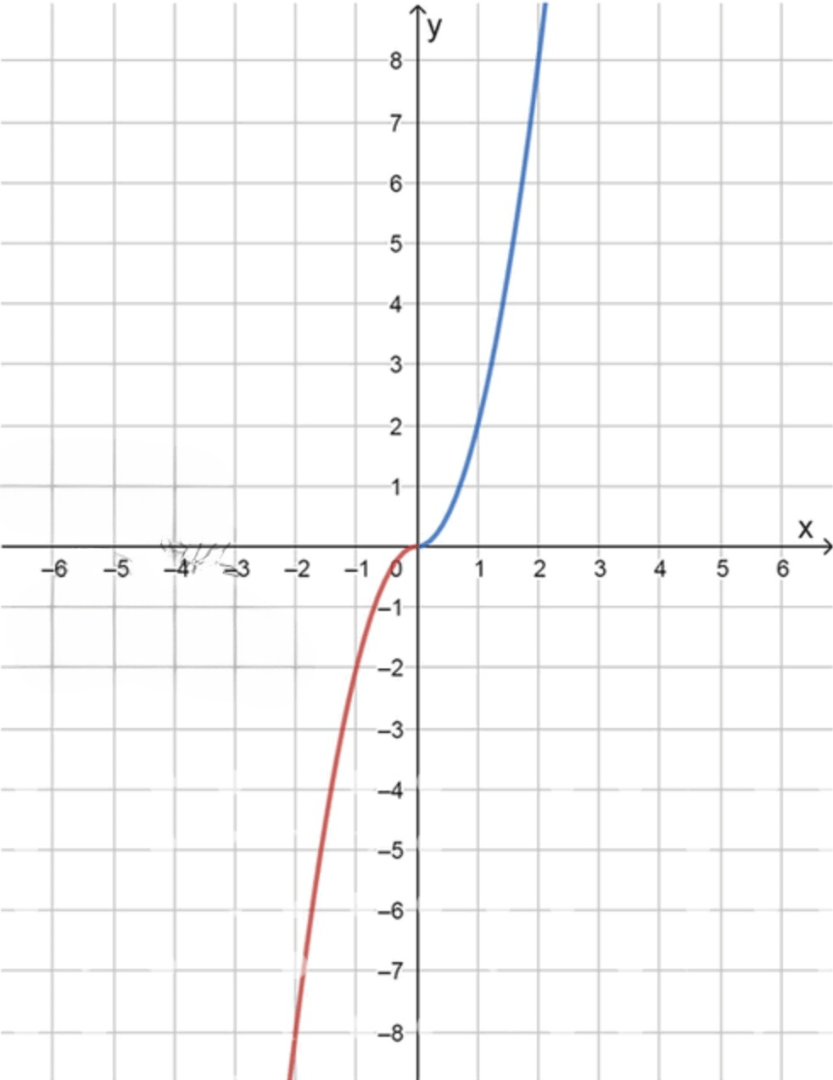
б)y = { 2 x 2 , если x ⩾ 0 , − 2 x 2 , если x < 0 ; x 0 = 0. y = \begin{cases} 2x^2, & \text{если } x \geqslant 0, \\ -2x^2, & \text{если } x < 0; \end{cases} \quad x_0 = 0.
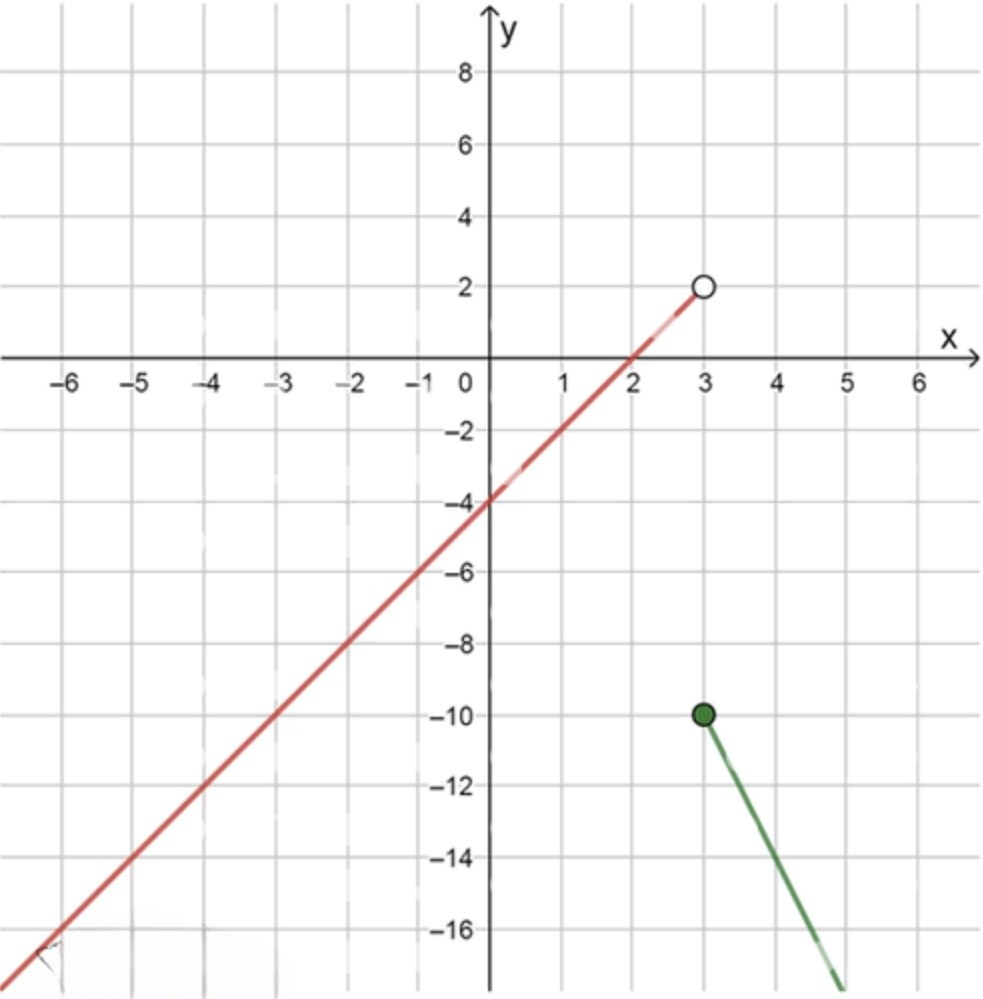
в)y = { − 4 x + 2 , если x ⩾ 3 , 2 x − 4 , если x < 3 ; x 0 = 3. y = \begin{cases} -4x + 2, & \text{если } x \geqslant 3, \\ 2x — 4, & \text{если } x < 3; \end{cases} \quad x_0 = 3.
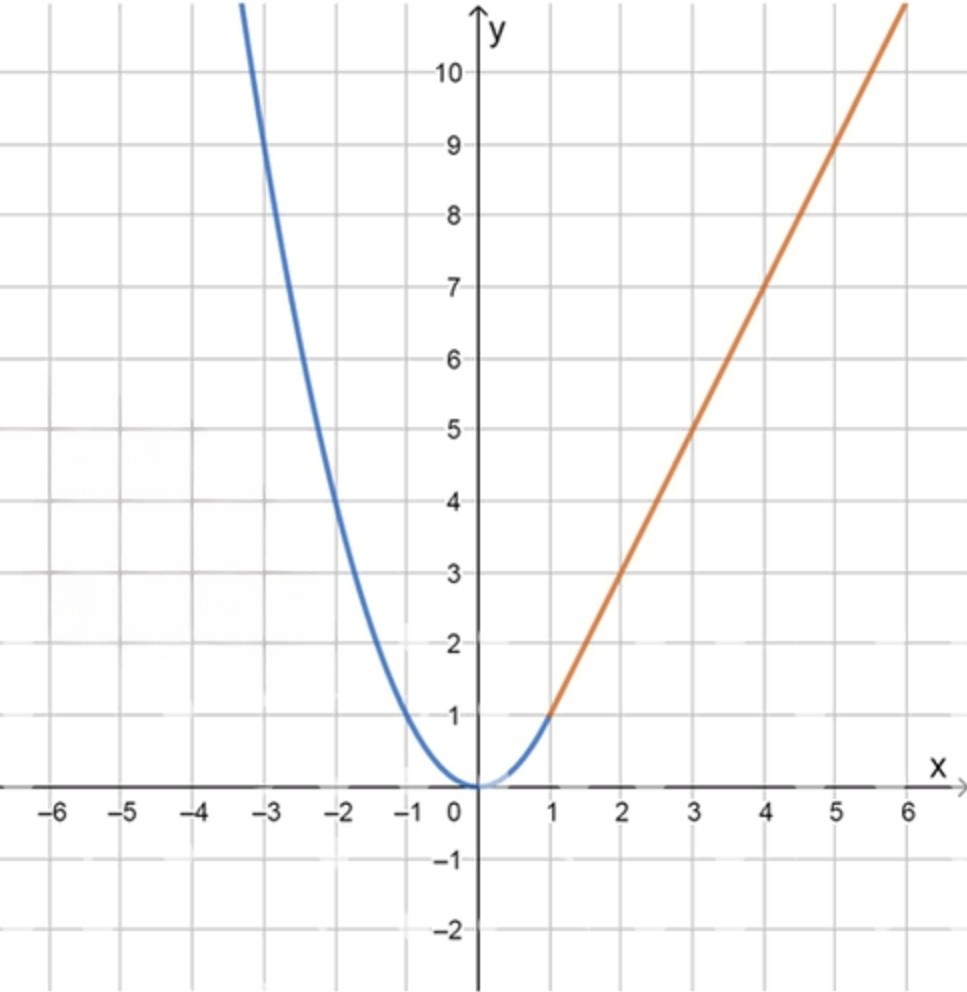
г)y = { x 2 , если x ⩽ 1 , 2 x − 1 , если x > 1 ; x 0 = 1.
Краткий ответ:
а)
y = { 3 x , если x ≥ 0 − 2 x + 3 , если x < 0 , x 0 = 0 ; y = \begin{cases} 3x, & \text{если } x \geq 0 \\ -2x + 3, & \text{если } x < 0 \end{cases}, \quad x_0 = 0;
График функции:
x − 2 0 0 2 y 7 3 0 6 \begin{array}{c|c c c c} x & -2 & 0 & 0 & 2 \\ \hline y & 7 & 3 & 0 & 6 \\ \end{array}
Точка x 0 = 0 x_0 = 0
Ответ: не существует.
б)
y = { 2 x 2 , если x ≥ 0 − 2 x 2 , если x < 0 , x 0 = 0 ; y = \begin{cases} 2x^2, & \text{если } x \geq 0 \\ -2x^2, & \text{если } x < 0 \end{cases}, \quad x_0 = 0;
График функции:
x − 2 − 1 0 0 1 2 y − 8 − 2 0 0 2 8 \begin{array}{c|c c c c c c} x & -2 & -1 & 0 & 0 & 1 & 2 \\ \hline y & -8 & -2 & 0 & 0 & 2 & 8 \\ \end{array}
Искомая точка принадлежит функции y = 2 x 2 y = 2x^2
Δ y Δ x = f ( x + Δ x ) − f ( x ) Δ x = 2 ( x + Δ x ) 2 − 2 x 2 Δ x = \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) — f(x)}{\Delta x} = \frac{2(x + \Delta x)^2 — 2x^2}{\Delta x} = = 2 x 2 + 4 x Δ x + 2 ( Δ x ) 2 − 2 x 2 Δ x = 4 x Δ x + 2 ( Δ x ) 2 Δ x = 4 x + 2 Δ x ; = \frac{2x^2 + 4x \Delta x + 2(\Delta x)^2 — 2x^2}{\Delta x} = \frac{4x \Delta x + 2(\Delta x)^2}{\Delta x} = 4x + 2\Delta x;
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 ( 4 x + 2 Δ x ) = 4 ⋅ 0 + 2 ⋅ 0 = 0 ; \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} (4x + 2\Delta x) = 4 \cdot 0 + 2 \cdot 0 = 0;
Ответ: y ′ = 0 y’ = 0
в)
y = { − 4 x + 2 , если x ≥ 3 2 x − 4 , если x < 3 , x 0 = 3 ; y = \begin{cases} -4x + 2, & \text{если } x \geq 3 \\ 2x — 4, & \text{если } x < 3 \end{cases}, \quad x_0 = 3;
График функции:
x 2 3 3 4 y 0 2 − 10 − 14 \begin{array}{c|c c c c} x & 2 & 3 & 3 & 4 \\ \hline y & 0 & 2 & -10 & -14 \\ \end{array}
Точка x 0 = 3 x_0 = 3
Ответ: не существует.
г)
y = { x 2 , если x ≤ 1 2 x − 1 , если x > 1 , x 0 = 1 ; y = \begin{cases} x^2, & \text{если } x \leq 1 \\ 2x — 1, & \text{если } x > 1 \end{cases}, \quad x_0 = 1;
График функции:
x − 3 − 2 − 1 0 1 1 2 y 9 4 1 0 1 1 3 \begin{array}{c|c c c c c c c} x & -3 & -2 & -1 & 0 & 1 & 1 & 2 \\ \hline y & 9 & 4 & 1 & 0 & 1 & 1 & 3 \\ \end{array}
Искомая точка принадлежит функции y = x 2 y = x^2
Δ y Δ x = f ( x + Δ x ) − f ( x ) Δ x = ( x + Δ x ) 2 − x 2 Δ x = \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) — f(x)}{\Delta x} = \frac{(x + \Delta x)^2 — x^2}{\Delta x} = = x 2 + 2 x Δ x + ( Δ x ) 2 − x 2 Δ x = 2 x Δ x + ( Δ x ) 2 Δ x = 2 x + Δ x ; = \frac{x^2 + 2x \Delta x + (\Delta x)^2 — x^2}{\Delta x} = \frac{2x \Delta x + (\Delta x)^2}{\Delta x} = 2x + \Delta x;
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 ( 2 x + Δ x ) = 2 ⋅ 1 + 0 = 2 ; \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} (2x + \Delta x) = 2 \cdot 1 + 0 = 2;
Ответ: y ′ = 2 y’ = 2
Подробный ответ:
а)
y = { 3 x , если x ≥ 0 − 2 x + 3 , если x < 0 , x 0 = 0 ; y = \begin{cases} 3x, & \text{если } x \geq 0 \\ -2x + 3, & \text{если } x < 0 \end{cases}, \quad x_0 = 0;
1. Построение таблицы значений функции
Подставим значения x x
Если x = − 2 x = -2 x < 0 x < 0 y = − 2 x + 3 = − 2 ⋅ ( − 2 ) + 3 = 4 + 3 = 7 y = -2x + 3 = -2 \cdot (-2) + 3 = 4 + 3 = 7
Если x = 0 x = 0 x ≥ 0 x \geq 0 y = 3 x = 3 ⋅ 0 = 0 y = 3x = 3 \cdot 0 = 0
Если x = 0 x = 0 x < 0 x < 0 y = − 2 x + 3 = − 2 ⋅ 0 + 3 = 0 + 3 = 3 y = -2x + 3 = -2 \cdot 0 + 3 = 0 + 3 = 3
(Эта строка показывает несоответствие значений функции при x = 0 x = 0
Если x = 2 x = 2 x ≥ 0 x \geq 0 y = 3 x = 3 ⋅ 2 = 6 y = 3x = 3 \cdot 2 = 6
Таблица:
x − 2 0 0 2 y 7 3 0 6 \begin{array}{c|c c c c} x & -2 & 0 & 0 & 2 \\ \hline y & 7 & 3 & 0 & 6 \\ \end{array}
2. Анализ точки x 0 = 0 x_0 = 0
Проверим, существует ли предел функции слева и справа от точки x = 0 x = 0
Слева от 0:lim x → 0 − y = lim x → 0 − ( − 2 x + 3 ) = − 2 ⋅ 0 + 3 = 3 \lim_{x \to 0^-} y = \lim_{x \to 0^-} (-2x + 3) = -2 \cdot 0 + 3 = 3 Справа от 0:lim x → 0 + y = lim x → 0 + ( 3 x ) = 3 ⋅ 0 = 0 \lim_{x \to 0^+} y = \lim_{x \to 0^+} (3x) = 3 \cdot 0 = 0 Так как lim x → 0 − f ( x ) ≠ lim x → 0 + f ( x ) \lim_{x \to 0^-} f(x) \ne \lim_{x \to 0^+} f(x) разрывна в точке x = 0 x = 0 .
3. Вывод по производной
Поскольку функция разрывна в точке x = 0 x = 0 не существует .
Ответ: не существует.
б)
y = { 2 x 2 , если x ≥ 0 − 2 x 2 , если x < 0 , x 0 = 0 ; y = \begin{cases} 2x^2, & \text{если } x \geq 0 \\ -2x^2, & \text{если } x < 0 \end{cases}, \quad x_0 = 0;
1. Таблица значений
x = − 2 x = -2 x < 0 x < 0 y = − 2 x 2 = − 2 ⋅ 4 = − 8 y = -2x^2 = -2 \cdot 4 = -8 x = − 1 x = -1 y = − 2 ⋅ 1 = − 2 y = -2 \cdot 1 = -2 x = 0 x = 0 x = 0 x = 0 x ≥ 0 x \geq 0 y = 2 ⋅ 0 2 = 0 y = 2 \cdot 0^2 = 0 (Дополнительно: x = 0 x = 0 x < 0 x < 0 y = − 2 ⋅ 0 2 = 0 y = -2 \cdot 0^2 = 0 x = 1 x = 1 y = 2 ⋅ 1 = 2 y = 2 \cdot 1 = 2 x = 2 x = 2 y = 2 ⋅ 4 = 8 y = 2 \cdot 4 = 8 Таблица:
x − 2 − 1 0 0 1 2 y − 8 − 2 0 0 2 8 \begin{array}{c|c c c c c c} x & -2 & -1 & 0 & 0 & 1 & 2 \\ \hline y & -8 & -2 & 0 & 0 & 2 & 8 \\ \end{array}
2. Принадлежность точки
Так как x 0 = 0 ∈ [ 0 , + ∞ ) x_0 = 0 \in [0, +\infty) y = 2 x 2 y = 2x^2
3. Производная через приращение
Формула приращения:
Δ y Δ x = f ( x + Δ x ) − f ( x ) Δ x \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) — f(x)}{\Delta x}
Подставляем f ( x ) = 2 x 2 f(x) = 2x^2
f ( x + Δ x ) = 2 ( x + Δ x ) 2 = 2 ( x 2 + 2 x Δ x + ( Δ x ) 2 ) = 2 x 2 + 4 x Δ x + 2 ( Δ x ) 2 f(x + \Delta x) = 2(x + \Delta x)^2 = 2(x^2 + 2x \Delta x + (\Delta x)^2) = 2x^2 + 4x \Delta x + 2(\Delta x)^2
Вычитаем:
f ( x + Δ x ) − f ( x ) Δ x = ( 2 x 2 + 4 x Δ x + 2 ( Δ x ) 2 ) − 2 x 2 Δ x = 4 x Δ x + 2 ( Δ x ) 2 Δ x = 4 x + 2 Δ x \frac{f(x + \Delta x) — f(x)}{\Delta x} = \frac{(2x^2 + 4x \Delta x + 2(\Delta x)^2) — 2x^2}{\Delta x} = \frac{4x \Delta x + 2(\Delta x)^2}{\Delta x} = 4x + 2\Delta x
4. Предел при Δ x → 0 \Delta x \to 0
lim Δ x → 0 ( 4 x + 2 Δ x ) = 4 x + 0 = 4 ⋅ 0 = 0 \lim_{\Delta x \to 0} (4x + 2\Delta x) = 4x + 0 = 4 \cdot 0 = 0
Ответ: y ′ = 0 y’ = 0
в)
y = { − 4 x + 2 , если x ≥ 3 2 x − 4 , если x < 3 , x 0 = 3 ; y = \begin{cases} -4x + 2, & \text{если } x \geq 3 \\ 2x — 4, & \text{если } x < 3 \end{cases}, \quad x_0 = 3;
1. Таблица значений
x = 2 x = 2 x < 3 x < 3 y = 2 x − 4 = 2 ⋅ 2 − 4 = 0 y = 2x — 4 = 2 \cdot 2 — 4 = 0 x = 3 x = 3 x ≥ 3 x \geq 3 y = − 4 x + 2 = − 4 ⋅ 3 + 2 = − 12 + 2 = − 10 y = -4x + 2 = -4 \cdot 3 + 2 = -12 + 2 = -10 x = 3 x = 3 x < 3 x < 3 y = 2 x − 4 = 2 ⋅ 3 − 4 = 6 − 4 = 2 y = 2x — 4 = 2 \cdot 3 — 4 = 6 — 4 = 2 x = 4 x = 4 y = − 4 x + 2 = − 4 ⋅ 4 + 2 = − 16 + 2 = − 14 y = -4x + 2 = -4 \cdot 4 + 2 = -16 + 2 = -14 Таблица:
x 2 3 3 4 y 0 2 − 10 − 14 \begin{array}{c|c c c c} x & 2 & 3 & 3 & 4 \\ \hline y & 0 & 2 & -10 & -14 \\ \end{array}
2. Анализ точки
Проверим предел функции:
Слева от 3:lim x → 3 − y = 2 x − 4 = 6 − 4 = 2 \lim_{x \to 3^-} y = 2x — 4 = 6 — 4 = 2 Справа от 3:lim x → 3 + y = − 4 x + 2 = − 12 + 2 = − 10 \lim_{x \to 3^+} y = -4x + 2 = -12 + 2 = -10 Точка разрыва → производная не существует .
Ответ: не существует.
г)
y = { x 2 , если x ≤ 1 2 x − 1 , если x > 1 , x 0 = 1 ; y = \begin{cases} x^2, & \text{если } x \leq 1 \\ 2x — 1, & \text{если } x > 1 \end{cases}, \quad x_0 = 1;
1. Таблица значений
x = − 3 x = -3 y = ( − 3 ) 2 = 9 y = (-3)^2 = 9 x = − 2 x = -2 y = 4 y = 4 x = − 1 x = -1 y = 1 y = 1 x = 0 x = 0 y = 0 y = 0 x = 1 x = 1 x ≤ 1 x \leq 1 y = 1 2 = 1 y = 1^2 = 1 x = 1 x = 1 x > 1 x > 1 y = 2 ⋅ 1 − 1 = 1 y = 2 \cdot 1 — 1 = 1 x = 2 x = 2 y = 2 ⋅ 2 − 1 = 4 − 1 = 3 y = 2 \cdot 2 — 1 = 4 — 1 = 3 Таблица:
x − 3 − 2 − 1 0 1 1 2 y 9 4 1 0 1 1 3 \begin{array}{c|c c c c c c c} x & -3 & -2 & -1 & 0 & 1 & 1 & 2 \\ \hline y & 9 & 4 & 1 & 0 & 1 & 1 & 3 \\ \end{array}
2. Принадлежность точки
x = 1 ∈ ( − ∞ , 1 ] ⇒ x = 1 \in (-\infty, 1] \Rightarrow y = x 2 y = x^2
3. Производная по определению
Δ y Δ x = f ( x + Δ x ) − f ( x ) Δ x \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) — f(x)}{\Delta x}
Для f ( x ) = x 2 f(x) = x^2
f ( x + Δ x ) = ( x + Δ x ) 2 = x 2 + 2 x Δ x + ( Δ x ) 2 f(x + \Delta x) = (x + \Delta x)^2 = x^2 + 2x\Delta x + (\Delta x)^2
Подставим:
f ( x + Δ x ) − f ( x ) Δ x = x 2 + 2 x Δ x + ( Δ x ) 2 − x 2 Δ x = 2 x Δ x + ( Δ x ) 2 Δ x = 2 x + Δ x \frac{f(x + \Delta x) — f(x)}{\Delta x} = \frac{x^2 + 2x \Delta x + (\Delta x)^2 — x^2}{\Delta x} = \frac{2x \Delta x + (\Delta x)^2}{\Delta x} = 2x + \Delta x
4. Предел при Δ x → 0 \Delta x \to 0
lim Δ x → 0 ( 2 x + Δ x ) = 2 x + 0 \lim_{\Delta x \to 0} (2x + \Delta x) = 2x + 0
Подставим x = 1 x = 1
2 ⋅ 1 = 2 2 \cdot 1 = 2
Ответ: y ′ = 2 y’ = 2