Краткий ответ:
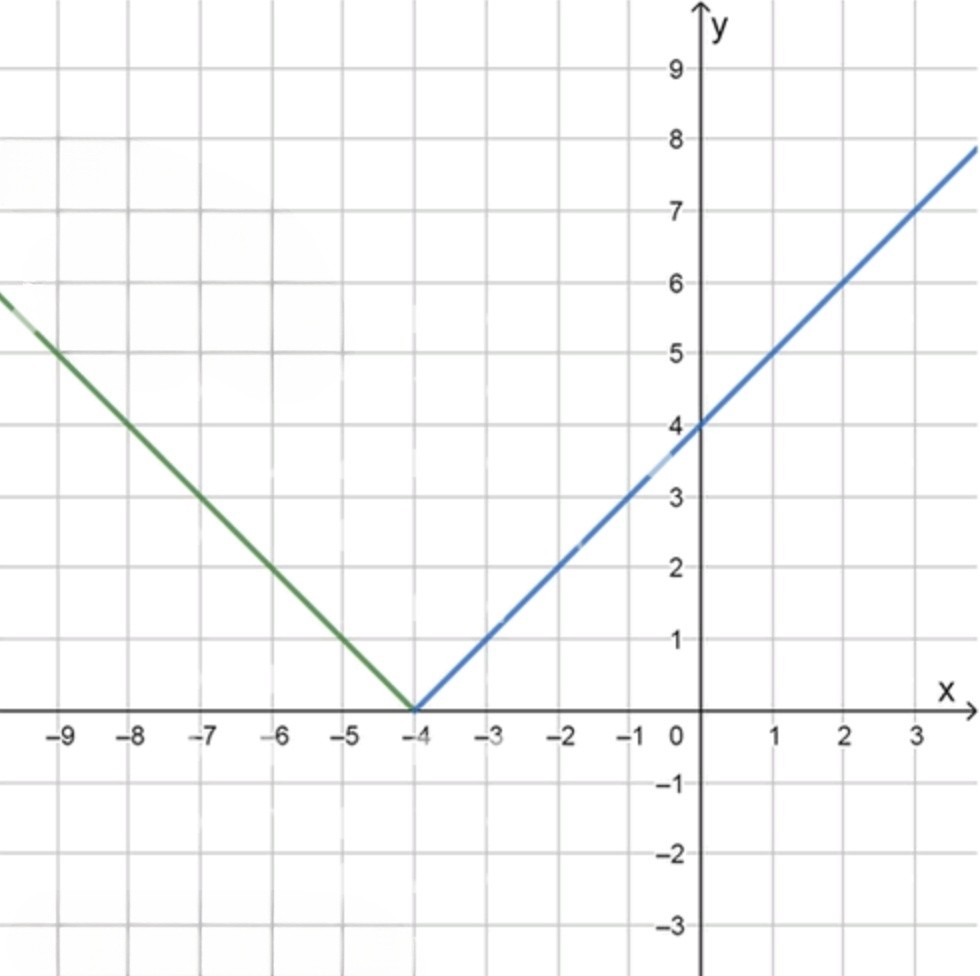
а) y = ∣ x + 4 ∣ , x 0 = − 4 y = |x + 4|, \quad x_0 = -4
По определению модуля числа:
y = { − x − 4 , если x < − 4 ; x + 4 , если x ≥ − 4 ; y = \begin{cases} -x — 4, & \text{если } x < -4; \\ x + 4, & \text{если } x \geq -4; \end{cases}
График функции:
x − 6 − 4 − 2 y 2 0 2 \begin{array}{|c|c|c|c|} \hline x & -6 & -4 & -2 \\ \hline y & 2 & 0 & 2 \\ \hline \end{array}
Точка x 0 = − 4 x_0 = -4
Ответ: не существует.
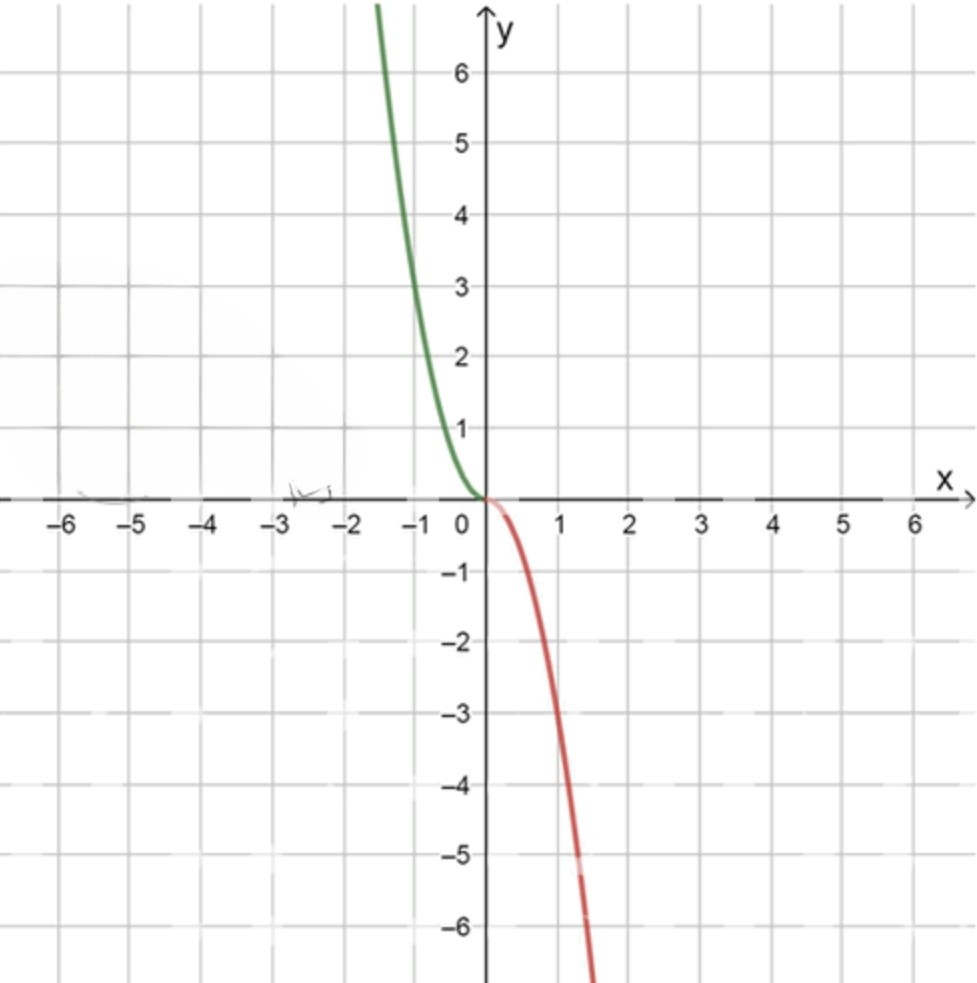
б) y = − 3 x ∣ x ∣ , x 0 = 0 y = -3x|x|, \quad x_0 = 0
По определению модуля числа:
y = { 3 x 2 , если x < 0 ; − 3 x 2 , если x ≥ 0 ; y = \begin{cases} 3x^2, & \text{если } x < 0; \\ -3x^2, & \text{если } x \geq 0; \end{cases}
График функции:
x − 1 0 1 y 3 0 − 3 \begin{array}{|c|c|c|c|} \hline x & -1 & 0 & 1 \\ \hline y & 3 & 0 & -3 \\ \hline \end{array}
Искомая точка принадлежит функции y = − 3 x 2 y = -3x^2
Δ y Δ x = f ( x 0 + Δ x ) − f ( x 0 ) Δ x = − 3 ( 0 + Δ x ) 2 + 3 ⋅ 0 2 Δ x = − 3 ( Δ x ) 2 Δ x = − 3 Δ x ; \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \Delta x) — f(x_0)}{\Delta x} = \frac{-3(0 + \Delta x)^2 + 3 \cdot 0^2}{\Delta x} = \frac{-3(\Delta x)^2}{\Delta x} = -3\Delta x;
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 ( − 3 Δ x ) = − 3 ⋅ 0 = 0 ; \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} (-3\Delta x) = -3 \cdot 0 = 0;
Ответ: y ′ = 0 y’ = 0
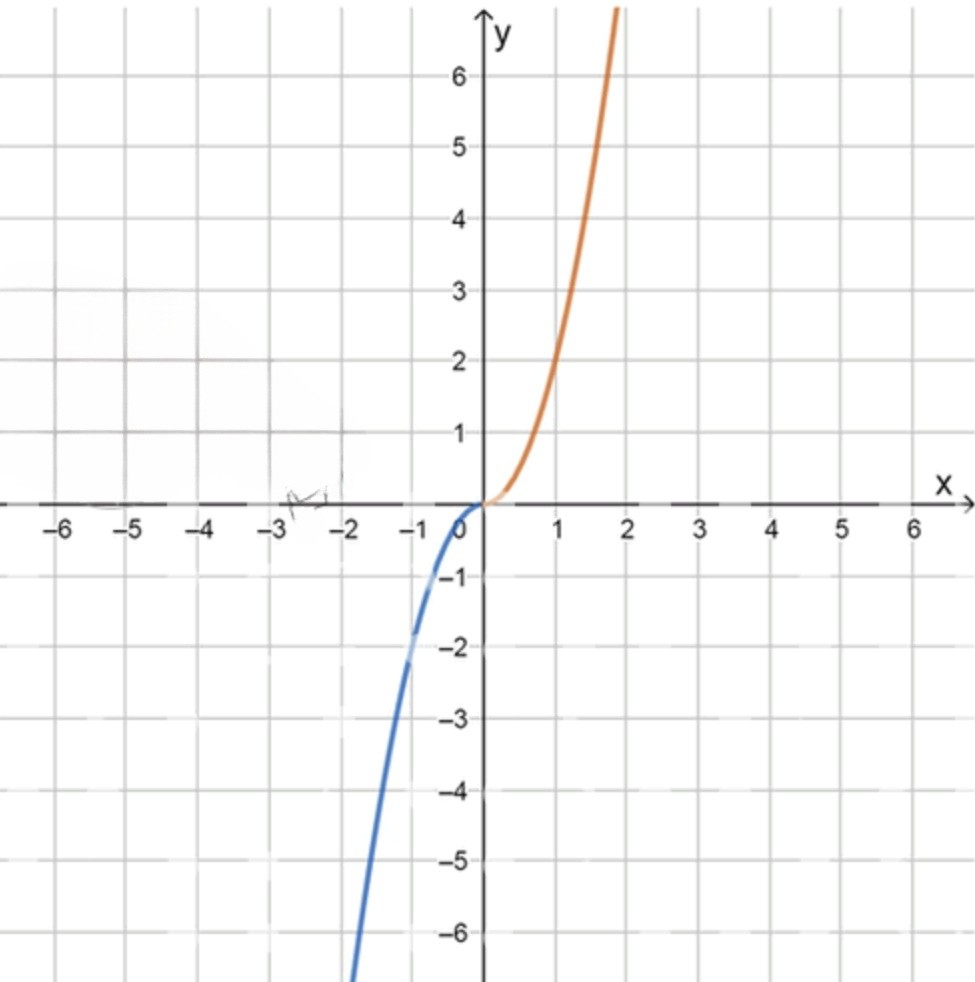
в) y = 2 x ∣ x ∣ , x 0 = 0 y = 2x|x|, \quad x_0 = 0
По определению модуля числа:
y = { − 2 x 2 , если x < 0 ; 2 x 2 , если x ≥ 0 ; y = \begin{cases} -2x^2, & \text{если } x < 0; \\ 2x^2, & \text{если } x \geq 0; \end{cases}
График функции:
x − 1 0 1 y − 2 0 2 \begin{array}{|c|c|c|c|} \hline x & -1 & 0 & 1 \\ \hline y & -2 & 0 & 2 \\ \hline \end{array}
Искомая точка принадлежит функции y = 2 x 2 y = 2x^2
Δ y Δ x = f ( x 0 + Δ x ) − f ( x 0 ) Δ x = 2 ( 0 + Δ x ) 2 + 2 ⋅ 0 2 Δ x = 2 ( Δ x ) 2 Δ x = 2 Δ x ; \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \Delta x) — f(x_0)}{\Delta x} = \frac{2(0 + \Delta x)^2 + 2 \cdot 0^2}{\Delta x} = \frac{2(\Delta x)^2}{\Delta x} = 2\Delta x;
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 2 Δ x = 2 ⋅ 0 = 0 ; \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} 2\Delta x = 2 \cdot 0 = 0;
Ответ: y ′ = 0 y’ = 0
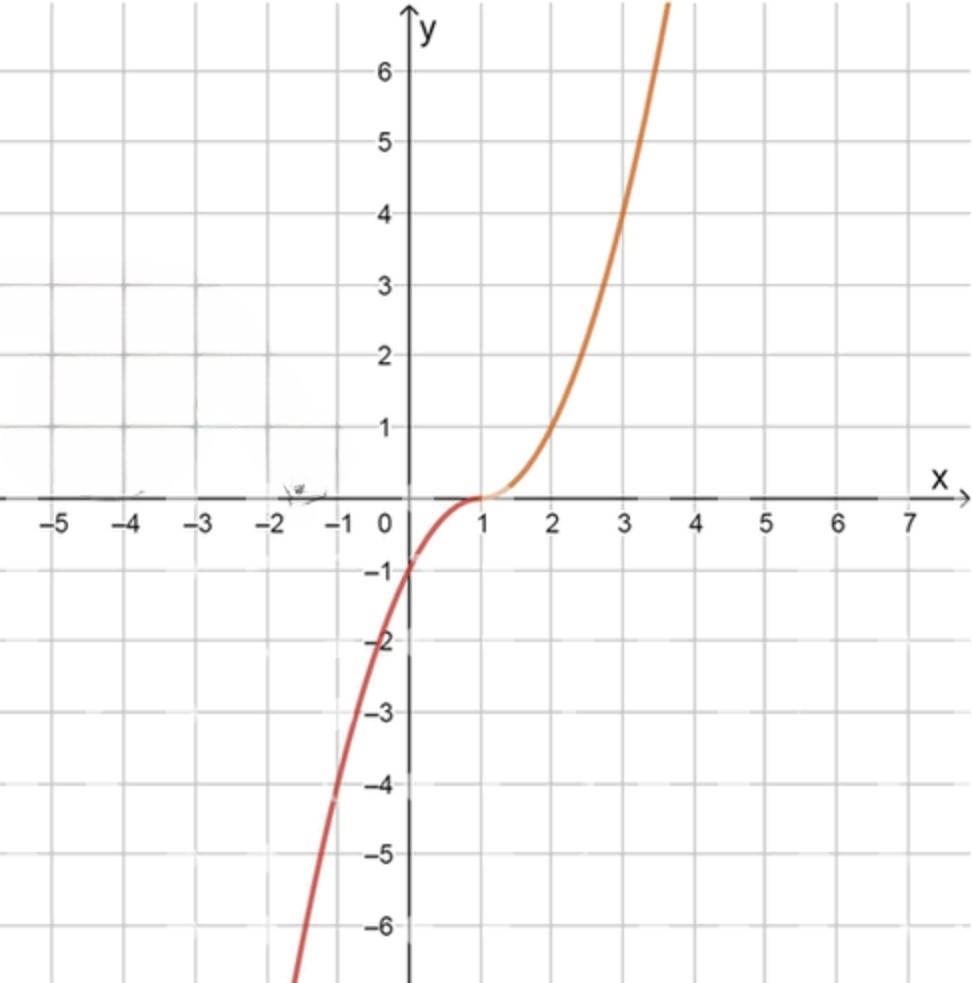
г) y = ( x − 1 ) ∣ x − 1 ∣ , x 0 = 1 y = (x — 1)|x — 1|, \quad x_0 = 1
По определению модуля числа:
y = { − ( x − 1 ) 2 , если x < 1 ; ( x − 1 ) 2 , если x ≥ 1 ; y = \begin{cases} -(x — 1)^2, & \text{если } x < 1; \\ (x — 1)^2, & \text{если } x \geq 1; \end{cases}
График функции:
x − 1 0 1 2 3 y − 4 − 1 0 1 4 \begin{array}{|c|c|c|c|c|c|} \hline x & -1 & 0 & 1 & 2 & 3 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \hline \end{array}
Искомая точка принадлежит функции y = ( x − 1 ) 2 y = (x — 1)^2
Δ y Δ x = f ( x 0 + Δ x ) − f ( x 0 ) Δ x = ( 1 − 1 + Δ x ) 2 − ( 1 − 1 ) 2 Δ x = ( Δ x ) 2 Δ x = Δ x ; \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \Delta x) — f(x_0)}{\Delta x} = \frac{(1 — 1 + \Delta x)^2 — (1 — 1)^2}{\Delta x} = \frac{(\Delta x)^2}{\Delta x} = \Delta x;
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 Δ x = 0 ; \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \Delta x = 0;
Ответ: y ′ = 0 y’ = 0
Подробный ответ:
Для решения задачи будем использовать определение:
f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) — f(x_0)}{\Delta x}
а) y = ∣ x + 4 ∣ , x 0 = − 4 y = |x + 4|, \quad x_0 = -4
1. Раскрытие модуля
Модуль ∣ x + 4 ∣ |x + 4|
∣ x + 4 ∣ = { − ( x + 4 ) , если x < − 4 ; x + 4 , если x ≥ − 4. |x + 4| = \begin{cases} -(x + 4), & \text{если } x < -4; \\ x + 4, & \text{если } x \geq -4. \end{cases}
То есть:
y = { − x − 4 , x < − 4 ; x + 4 , x ≥ − 4. y = \begin{cases} -x — 4, & x < -4; \\ x + 4, & x \geq -4. \end{cases}
2. Поведение слева и справа от точки x 0 = − 4 x_0 = -4
Слева от точки (при x < − 4 x < -4 y = − x − 4 y = -x — 4 y ′ = − 1 y’ = -1 Справа от точки (при x > − 4 x > -4 y = x + 4 y = x + 4 y ′ = 1 y’ = 1 3. Проверим производную по определению с обеих сторон
Слева:
f − ′ ( − 4 ) = lim Δ x → 0 − f ( − 4 + Δ x ) − f ( − 4 ) Δ x f’_{-}(-4) = \lim_{\Delta x \to 0^-} \frac{f(-4 + \Delta x) — f(-4)}{\Delta x}
При Δ x < 0 \Delta x < 0 − 4 + Δ x < − 4 -4 + \Delta x < -4
f ( − 4 + Δ x ) = − ( − 4 + Δ x ) − 4 = 4 − Δ x − 4 = − Δ x f(-4 + \Delta x) = -(-4 + \Delta x) — 4 = 4 — \Delta x — 4 = -\Delta x f ( − 4 ) = ∣ − 4 + 4 ∣ = ∣ 0 ∣ = 0 f(-4) = |-4 + 4| = |0| = 0 f ( − 4 + Δ x ) − f ( − 4 ) Δ x = − Δ x − 0 Δ x = − 1 \frac{f(-4 + \Delta x) — f(-4)}{\Delta x} = \frac{-\Delta x — 0}{\Delta x} = -1
Справа:
f + ′ ( − 4 ) = lim Δ x → 0 + f ( − 4 + Δ x ) − f ( − 4 ) Δ x f’_{+}(-4) = \lim_{\Delta x \to 0^+} \frac{f(-4 + \Delta x) — f(-4)}{\Delta x}
При Δ x > 0 \Delta x > 0 − 4 + Δ x > − 4 -4 + \Delta x > -4
f ( − 4 + Δ x ) = ( − 4 + Δ x ) + 4 = Δ x f(-4 + \Delta x) = (-4 + \Delta x) + 4 = \Delta x f ( − 4 + Δ x ) − f ( − 4 ) Δ x = Δ x − 0 Δ x = 1 \frac{f(-4 + \Delta x) — f(-4)}{\Delta x} = \frac{\Delta x — 0}{\Delta x} = 1
4. Сравнение односторонних производных:
f − ′ ( − 4 ) = − 1 , f + ′ ( − 4 ) = 1 ⇒ не совпадают f’_{-}(-4) = -1, \quad f’_{+}(-4) = 1 \Rightarrow \text{не совпадают}
5. Вывод:
Предел слева и справа не равны → производная не существует.
Ответ: не существует.
б) y = − 3 x ∣ x ∣ , x 0 = 0 y = -3x|x|, \quad x_0 = 0
1. Раскроем модуль ∣ x ∣ |x|
∣ x ∣ = { − x , x < 0 ; x , x ≥ 0. ⇒ y = { − 3 x ⋅ ( − x ) = 3 x 2 , x < 0 ; − 3 x ⋅ x = − 3 x 2 , x ≥ 0. |x| = \begin{cases} -x, & x < 0; \\ x, & x \geq 0. \end{cases} \Rightarrow y = \begin{cases} -3x \cdot (-x) = 3x^2, & x < 0; \\ -3x \cdot x = -3x^2, & x \geq 0. \end{cases}
2. Найдём значение функции в точке:
y ( 0 ) = − 3 ⋅ 0 ⋅ ∣ 0 ∣ = 0 y(0) = -3 \cdot 0 \cdot |0| = 0
3. Вычислим по определению:
f ′ ( 0 ) = lim Δ x → 0 f ( 0 + Δ x ) − f ( 0 ) Δ x f'(0) = \lim_{\Delta x \to 0} \frac{f(0 + \Delta x) — f(0)}{\Delta x}
При Δ x > 0 \Delta x > 0
f ( 0 + Δ x ) = − 3 ( Δ x ) 2 ⇒ − 3 ( Δ x ) 2 − 0 Δ x = − 3 Δ x → 0 f(0 + \Delta x) = -3(\Delta x)^2 \Rightarrow \frac{-3(\Delta x)^2 — 0}{\Delta x} = -3\Delta x \to 0
При Δ x < 0 \Delta x < 0
f ( 0 + Δ x ) = 3 ( Δ x ) 2 ⇒ 3 ( Δ x ) 2 − 0 Δ x = 3 Δ x → 0 f(0 + \Delta x) = 3(\Delta x)^2 \Rightarrow \frac{3(\Delta x)^2 — 0}{\Delta x} = 3\Delta x \to 0
4. Предел с обеих сторон:
lim Δ x → 0 Δ y Δ x = 0 \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = 0
Ответ: y ′ = 0 y’ = 0
в) y = 2 x ∣ x ∣ , x 0 = 0 y = 2x|x|, \quad x_0 = 0
1. Раскроем модуль:
y = { 2 x ⋅ ( − x ) = − 2 x 2 , x < 0 ; 2 x ⋅ x = 2 x 2 , x ≥ 0 ; y = \begin{cases} 2x \cdot (-x) = -2x^2, & x < 0; \\ 2x \cdot x = 2x^2, & x \geq 0; \end{cases}
2. Найдём значение функции в точке:
f ( 0 ) = 0 f(0) = 0
3. Определение производной:
f ′ ( 0 ) = lim Δ x → 0 f ( Δ x ) − f ( 0 ) Δ x f'(0) = \lim_{\Delta x \to 0} \frac{f(\Delta x) — f(0)}{\Delta x}
Δ x > 0 \Delta x > 0
f ( Δ x ) = 2 ( Δ x ) 2 ⇒ 2 ( Δ x ) 2 Δ x = 2 Δ x → 0 f(\Delta x) = 2(\Delta x)^2 \Rightarrow \frac{2(\Delta x)^2}{\Delta x} = 2\Delta x \to 0
Δ x < 0 \Delta x < 0
f ( Δ x ) = − 2 ( Δ x ) 2 ⇒ − 2 ( Δ x ) 2 Δ x = − 2 Δ x → 0 f(\Delta x) = -2(\Delta x)^2 \Rightarrow \frac{-2(\Delta x)^2}{\Delta x} = -2\Delta x \to 0
4. Предел с обеих сторон:
lim Δ x → 0 Δ y Δ x = 0 \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = 0
Ответ: y ′ = 0 y’ = 0
г) y = ( x − 1 ) ∣ x − 1 ∣ , x 0 = 1 y = (x — 1)|x — 1|, \quad x_0 = 1
1. Раскроем модуль:
∣ x − 1 ∣ = { − ( x − 1 ) , x < 1 ; x − 1 , x ≥ 1 ; ⇒
y = { ( x − 1 ) ( − ( x − 1 ) ) = − ( x − 1 ) 2 , x < 1 ; ( x − 1 ) 2 , x ≥ 1. |x — 1| = \begin{cases} -(x — 1), & x < 1; \\ x — 1, & x \geq 1; \end{cases} \Rightarrow y = \begin{cases} (x — 1)(-(x — 1)) = -(x — 1)^2, & x < 1; \\ (x — 1)^2, & x \geq 1. \end{cases}
2. Значение функции в точке:
f ( 1 ) = ( 1 − 1 ) ∣ 1 − 1 ∣ = 0 f(1) = (1 — 1)|1 — 1| = 0
3. Производная по определению:
f ′ ( 1 ) = lim Δ x → 0 f ( 1 + Δ x ) − f ( 1 ) Δ x f'(1) = \lim_{\Delta x \to 0} \frac{f(1 + \Delta x) — f(1)}{\Delta x}
Δ x > 0 \Delta x > 0
f ( 1 + Δ x ) = ( 1 + Δ x − 1 ) 2 = ( Δ x ) 2 ⇒ ( Δ x ) 2 Δ x = Δ x → 0 f(1 + \Delta x) = (1 + \Delta x — 1)^2 = (\Delta x)^2 \Rightarrow \frac{(\Delta x)^2}{\Delta x} = \Delta x \to 0
Δ x < 0 \Delta x < 0
f ( 1 + Δ x ) = − ( Δ x ) 2 ⇒ − ( Δ x ) 2 Δ x = − Δ x → 0 f(1 + \Delta x) = -(\Delta x)^2 \Rightarrow \frac{- (\Delta x)^2}{\Delta x} = -\Delta x \to 0
4. Одинаковые пределы с обеих сторон:
f ′ ( 1 ) = 0 f'(1) = 0
Ответ: y ′ = 0 y’ = 0