ГДЗ по Алгебре 10 Класс Номер 41.36 Профильный Уровень Мордкович — Подробные Ответы

а) $y = x^2 — 5|x| + 6$, $x_0 = 2$, $x_1 = 3$, $x_2 = 0$;

По определению модуля числа:

$$y = \begin{cases} x^2 + 5x + 6, & \text{если } x < 0, \\ x^2 — 5x + 6, & \text{если } x \geq 0. \end{cases}$$

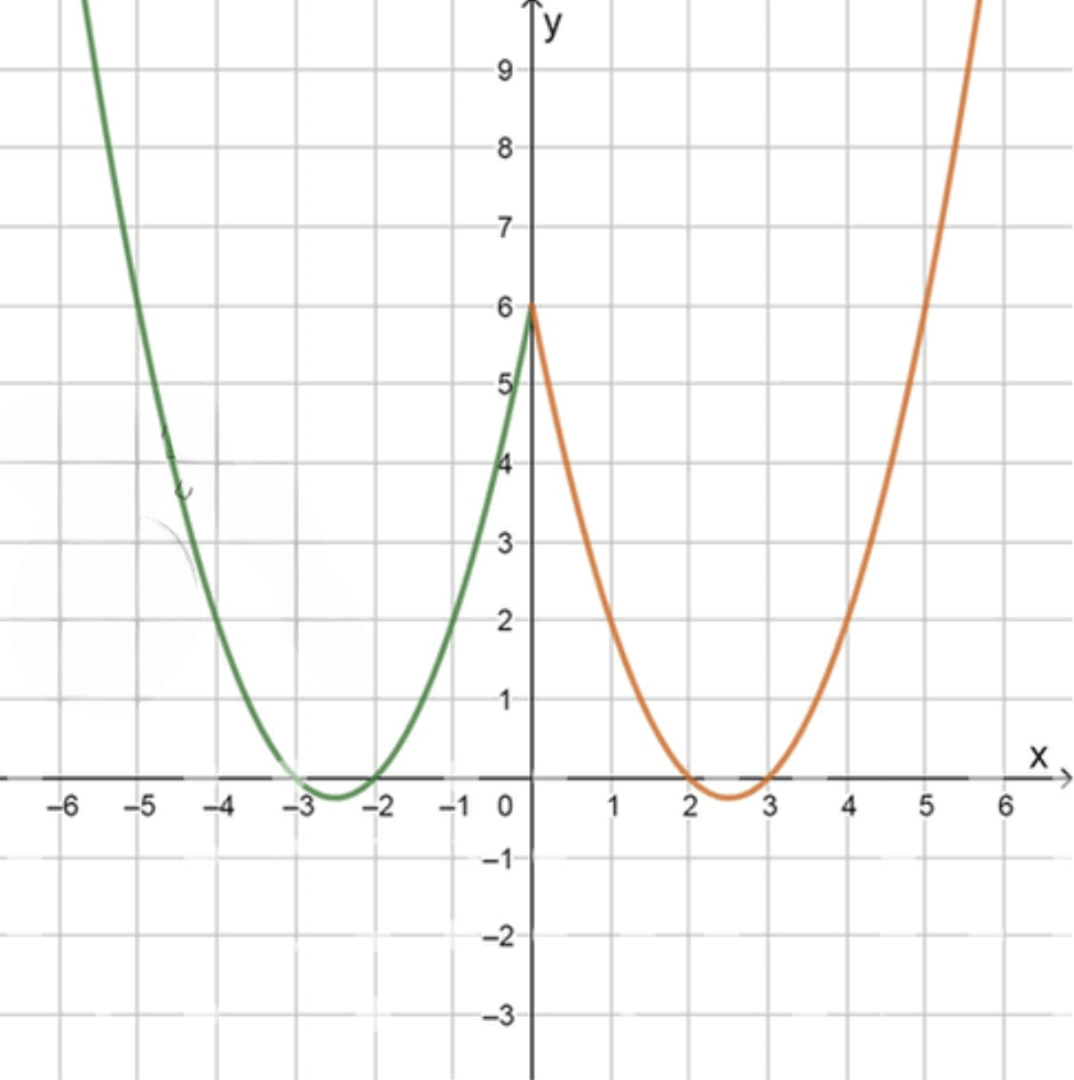
График функции:

$$\begin{array}{c|c c c c c c c c} x & -5 & -3 & -2 & 0 & 2 & 3 & 5 \\ \hline y & 6 & 0 & 0 & 6 & 0 & 0 & 6 \\ \end{array}$$

Все искомые точки принадлежат функции:

$$y = x^2 — 5x + 6;$$ $$y’ = (x^2)’ — (5x + 6)’ = 2x — 5;$$

Значения производной:

$$y'(2) = 2 \cdot 2 — 5 = 4 — 5 = -1;$$ $$y'(3) = 2 \cdot 3 — 5 = 6 — 5 = 1;$$ $$y'(0) \text{ — не существует (точка излома)};$$

Ответ: $-1; 1; \text{не существует}$.

б) $y = |x^2 — 5|x| + 6|$, $x_0 = -2$, $x_1 = 0$, $x_2 = 2,5$;

По определению модуля числа:

$$y = \begin{cases} |x^2 + 5x + 6|, & \text{если } x < 0, \\ |x^2 — 5x + 6|, & \text{если } x \geq 0. \end{cases}$$

$x^2 \pm 5x + 6 = 0$;

$$D = 5^2 — 4 \cdot 6 = 25 — 24 = 1, \text{ тогда: }$$ $$x_1 = \frac{5 — 1}{2} = 2 \quad \text{и} \quad x_2 = \frac{5 + 1}{2} = 3;$$ $$x_3 = \frac{-5 — 1}{2} = -3 \quad \text{и} \quad x_4 = \frac{-5 + 1}{2} = -2;$$ $$y = \begin{cases} -x^2 — 5x — 6, & \text{если } -3 < x < -2, \\ -x^2 + 5x — 6, & \text{если } 2 < x < 3, \\ x^2 + 5x + 6, & \text{если } x \in (-\infty; -3) \cup (-2; 0), \\ x^2 — 5x + 6, & \text{если } x \in (0; 2) \cup (3; +\infty). \end{cases}$$

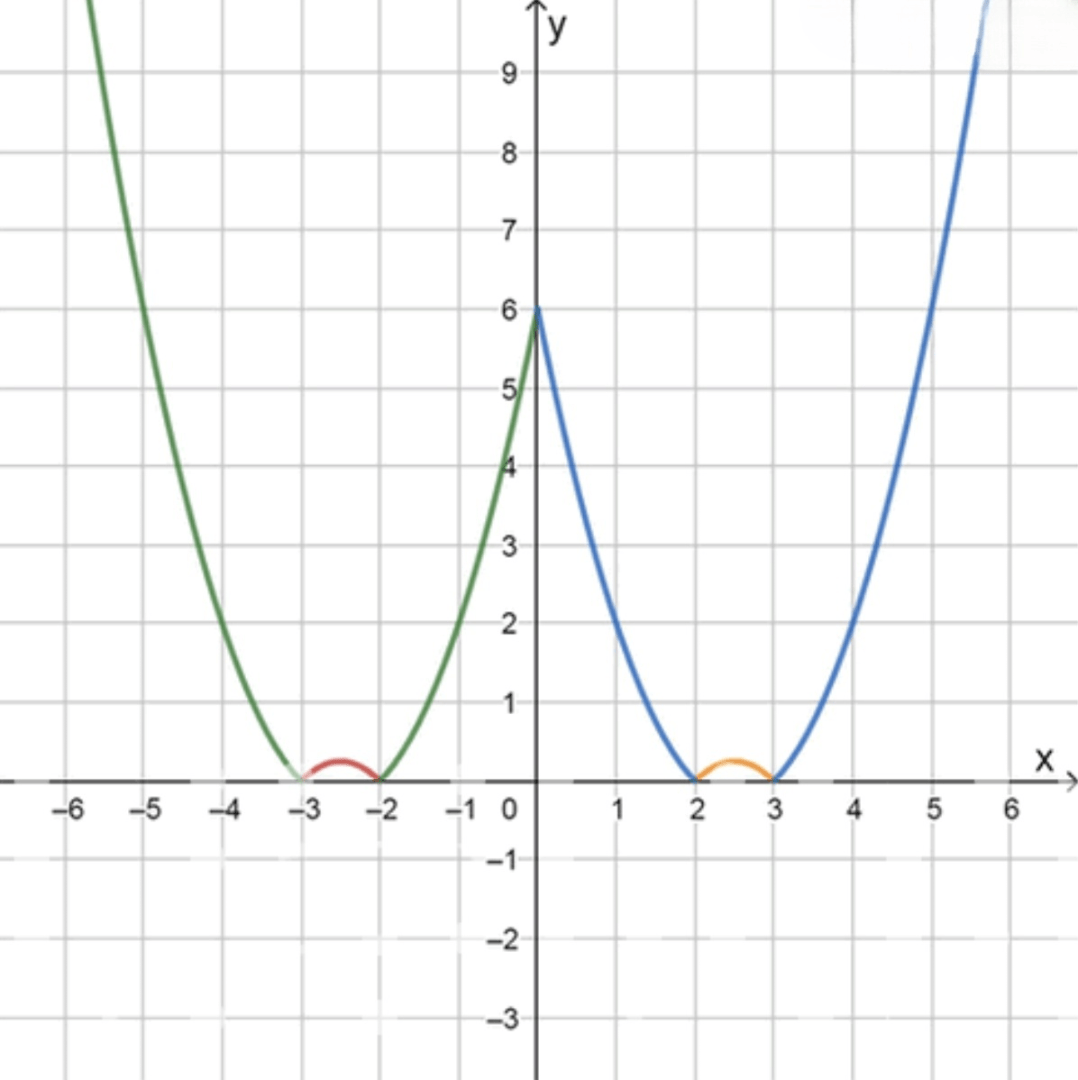
График функции:

$$\begin{array}{c|c c c c c c c c} x & -5 & -3 & -2,5 & -2 & 0 & 2 & 2,5 & 3 & 5 \\ \hline y & 6 & 0 & 0,25 & 0 & 6 & 0 & 0,25 & 0 & 6 \\ \end{array}$$

Точка $x_2 = 2,5$ принадлежит функции:

$$y = -x^2 + 5x — 6;$$ $$y’ = -(x^2)’ + (5x — 6)’ = -2x + 5;$$

Значения производной:

$$y'(-2) \text{ — не существует (точка излома)};$$ $$y'(0) \text{ — не существует (точка излома)};$$ $$y'(2,5) = -2 \cdot 2,5 + 5 = -5 + 5 = 0;$$

Ответ: $\text{не существует; не существует; } 0$.

а) $y = x^2 — 5|x| + 6$, $x_0 = 2$, $x_1 = 3$, $x_2 = 0$

1) Учитываем модуль: раскрытие $|x|$

Функция содержит выражение с модулем: $|x|$. Вспомним определение модуля:

$$|x| = \begin{cases} -x, & \text{если } x < 0, \\ x, & \text{если } x \geq 0. \end{cases}$$

Подставим это в выражение $y = x^2 — 5|x| + 6$. Разделим функцию на два случая:

Случай 1: $x < 0$

Тогда $|x| = -x$, значит:

$$y = x^2 — 5(-x) + 6 = x^2 + 5x + 6.$$

Случай 2: $x \geq 0$

Тогда $|x| = x$, значит:

$$y = x^2 — 5x + 6.$$

Итоговое определение функции:

$$y = \begin{cases} x^2 + 5x + 6, & \text{если } x < 0, \\ x^2 — 5x + 6, & \text{если } x \geq 0. \end{cases}$$

2) Построим таблицу значений функции

Для построения графика подставим значения $x$ в соответствующие формулы (учитывая знак $x$):

3) Проверим, к какой ветви функции относятся заданные точки

Нам даны:

• $x_0 = 2$: входит в ветвь $x \geq 0 \Rightarrow y = x^2 — 5x + 6$
• $x_1 = 3$: тоже $x \geq 0$
• $x_2 = 0$: граница разбиения, но $x \geq 0$, значит входит в ту же ветвь

Итак, все точки находятся в части функции $y = x^2 — 5x + 6$.

4) Найдём производную $y’$ функции $y = x^2 — 5x + 6$

Применим правило производной суммы:

$$y = x^2 — 5x + 6 \Rightarrow y’ = (x^2)’ — (5x)’ + (6)’ = 2x — 5 + 0 = 2x — 5$$

5) Вычислим производную в заданных точках

• В точке $x_0 = 2$:

$$y'(2) = 2 \cdot 2 — 5 = 4 — 5 = -1$$

• В точке $x_1 = 3$:

$$y'(3) = 2 \cdot 3 — 5 = 6 — 5 = 1$$

• В точке $x_2 = 0$:

Точка $x = 0$ — точка излома, потому что в ней меняется выражение функции (меняется определение модуля).

Чтобы понять, существует ли производная в точке $x = 0$, нужно проверить односторонние производные.

Слева от 0: $y = x^2 + 5x + 6 \Rightarrow y’ = 2x + 5 \Rightarrow y’_-(0) = 5$

Справа от 0: $y = x^2 — 5x + 6 \Rightarrow y’ = 2x — 5 \Rightarrow y’_+(0) = -5$

$$y’_-(0) \ne y’_+(0) \Rightarrow \text{производной не существует.}$$

6) Ответ для пункта а:

$$\boxed{-1; \quad 1; \quad \text{не существует}}$$

б) $y = |x^2 — 5|x| + 6|$, $x_0 = -2$, $x_1 = 0$, $x_2 = 2{,}5$

1) Раскроем модуль поэтапно

Внутри стоит выражение:

$$|x^2 — 5|x| + 6|$$

Сначала нужно раскрыть внутренний модуль $|x|$, затем разобраться, при каких значениях выражение внутри внешнего модуля положительно или отрицательно.

1.1) Раскроем внутренний модуль $|x|$:

• Для $x < 0$: $|x| = -x$,
• Для $x \geq 0$: $|x| = x$

Итак:

• $x < 0 \Rightarrow y = |x^2 + 5x + 6|$
• $x \geq 0 \Rightarrow y = |x^2 — 5x + 6|$

1.2) Найдём нули подмодульных выражений

• $x^2 — 5x + 6 = 0 \Rightarrow x = 2, 3$
• $x^2 + 5x + 6 = 0 \Rightarrow x = -2, -3$

2) Раскроем внешний модуль, исходя из знака выражения

Разобьём область определения на промежутки между найденными корнями:

$x < -3$: $x^2 + 5x + 6 > 0 \Rightarrow y = x^2 + 5x + 6$

$-3 < x < -2$: $x^2 + 5x + 6 < 0 \Rightarrow y = -(x^2 + 5x + 6)$

$-2 < x < 0$: $x^2 + 5x + 6 > 0 \Rightarrow y = x^2 + 5x + 6$

$0 < x < 2$: $x^2 — 5x + 6 > 0 \Rightarrow y = x^2 — 5x + 6$

$2 < x < 3$: $x^2 — 5x + 6 < 0 \Rightarrow y = -(x^2 — 5x + 6) = -x^2 + 5x — 6$

$x > 3$: $x^2 — 5x + 6 > 0 \Rightarrow y = x^2 — 5x + 6$

3) Уточним выражение функции:

$$y = \begin{cases} x^2 + 5x + 6, & x \in (-\infty; -3), \\ -x^2 — 5x — 6, & x \in (-3; -2), \\ x^2 + 5x + 6, & x \in (-2; 0), \\ x^2 — 5x + 6, & x \in (0; 2), \\ -x^2 + 5x — 6, & x \in (2; 3), \\ x^2 — 5x + 6, & x \in (3; +\infty). \end{cases}$$

4) Проверим, к каким выражениям принадлежат точки

• $x_0 = -2$ — граничная точка, но функция разная по разные стороны. Значит, возможна точка излома.
• $x_1 = 0$ — также граничная точка между двумя выражениями → проверим односторонние производные.
• $x_2 = 2{,}5 \in (2; 3) \Rightarrow y = -x^2 + 5x — 6$

5) Найдём производные для соответствующих выражений

$y = -x^2 + 5x — 6 \Rightarrow y’ = -2x + 5$

6) Вычислим производную в заданных точках

• $x = -2$:

Слева: $y = -x^2 — 5x — 6 \Rightarrow y’ = -2x — 5 \Rightarrow y’_-(-2) = 4 — 5 = -1$

Справа: $y = x^2 + 5x + 6 \Rightarrow y’ = 2x + 5 \Rightarrow y’_+(-2) = -4 + 5 = 1$

$\Rightarrow y’ \text{ не существует}$

• $x = 0$:

Слева: $y = x^2 + 5x + 6 \Rightarrow y’ = 2x + 5 \Rightarrow y’_-(0) = 5$

Справа: $y = x^2 — 5x + 6 \Rightarrow y’ = 2x — 5 \Rightarrow y’_+(0) = -5$

$\Rightarrow y’ \text{ не существует}$

• $x = 2{,}5$:

Точка принадлежит выражению $y = -x^2 + 5x — 6 \Rightarrow y’ = -2x + 5$

$$y'(2{,}5) = -2 \cdot 2{,}5 + 5 = -5 + 5 = 0$$

7) Ответ для пункта б:

$$\boxed{\text{не существует; не существует; } 0}$$