Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.18 Профильный Уровень Мордкович — Подробные Ответы
а)
б)
в)
г)
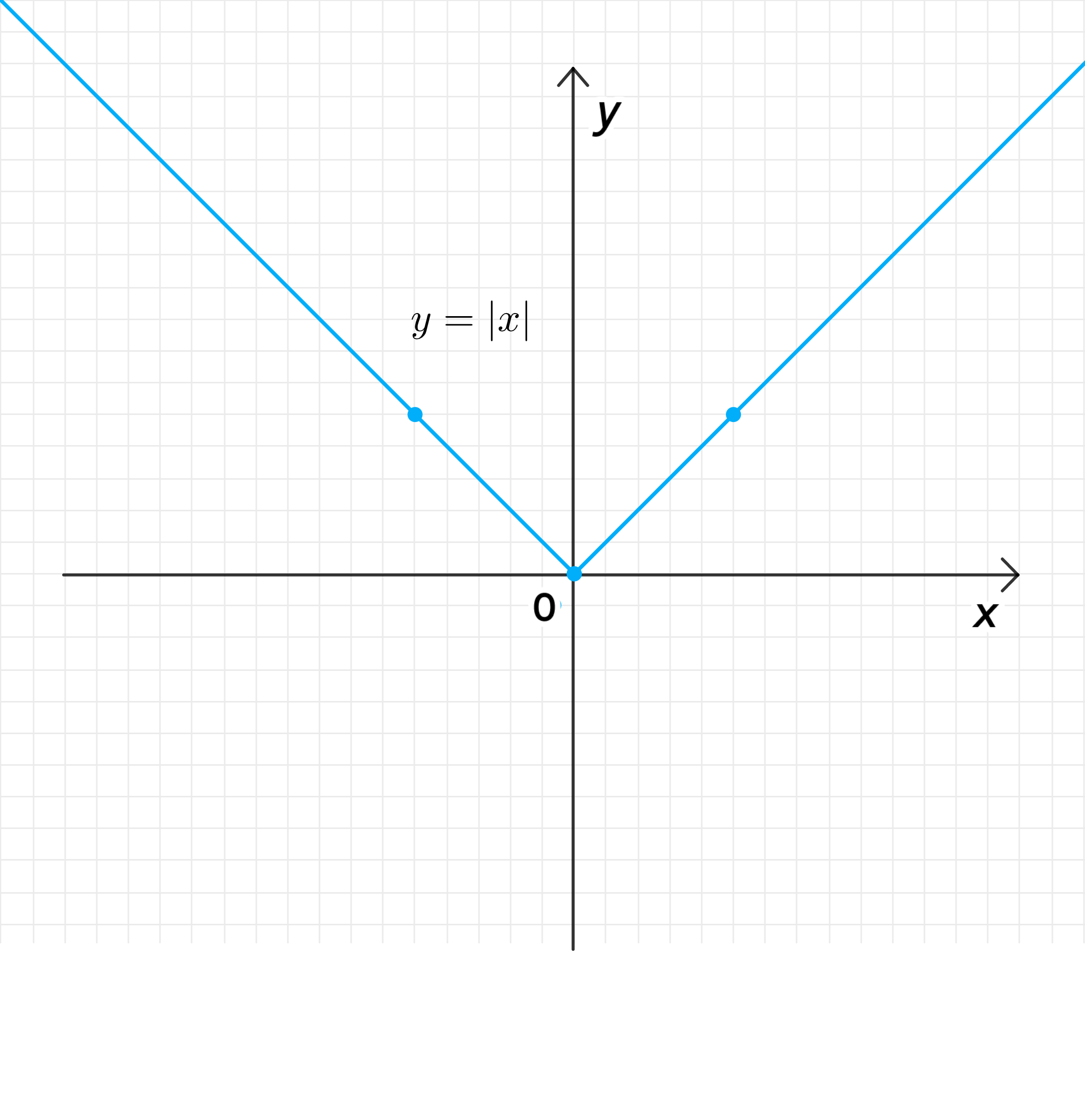
а)
Область определения: ;
Множество значений: ;
Координаты вершины модуля:
и ;
Координаты некоторых точек:
График функции:
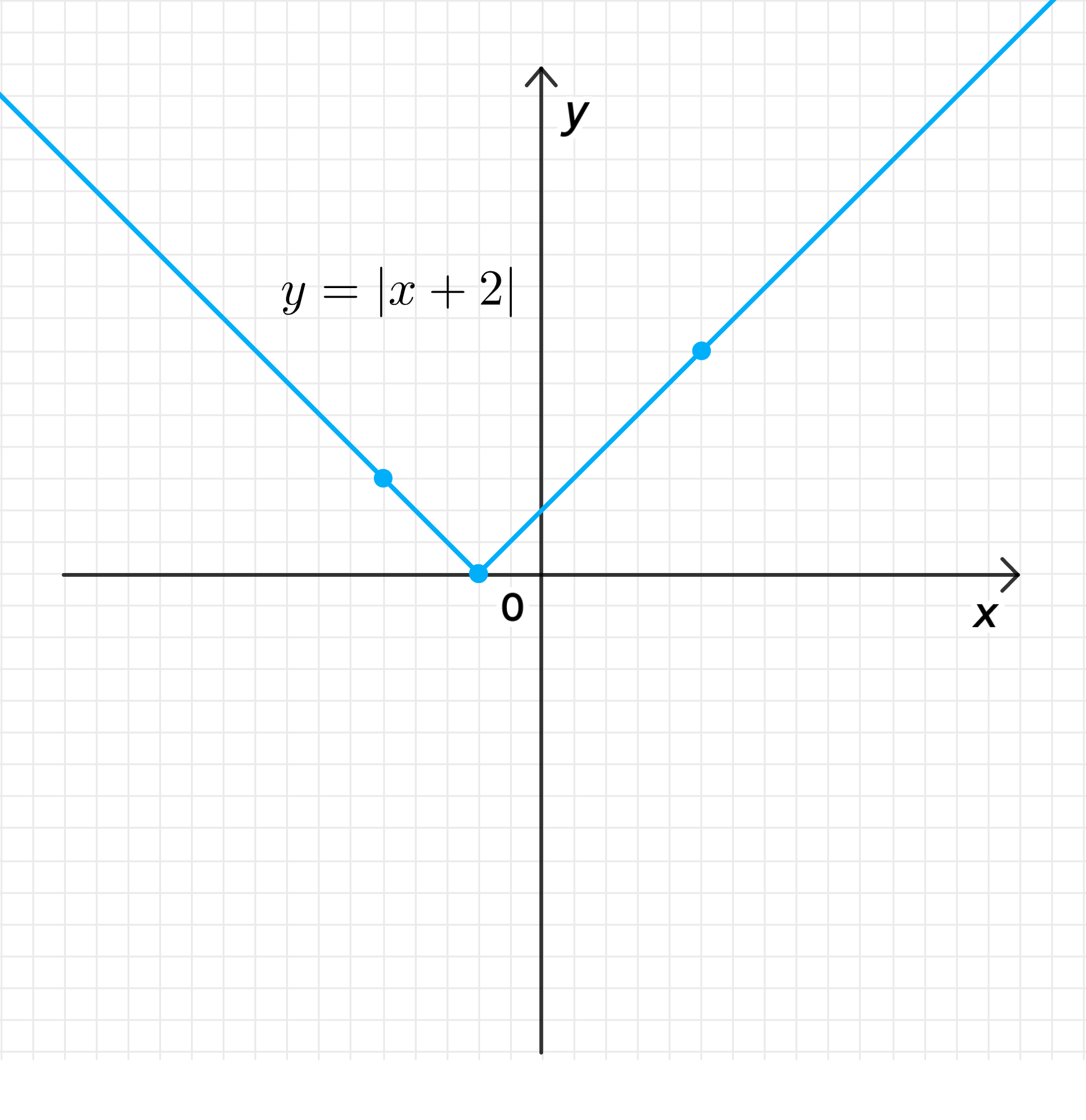
б)
Область определения: ;
Множество значений: ;
Координаты вершины модуля:
и ;
Координаты некоторых точек:
График функции:
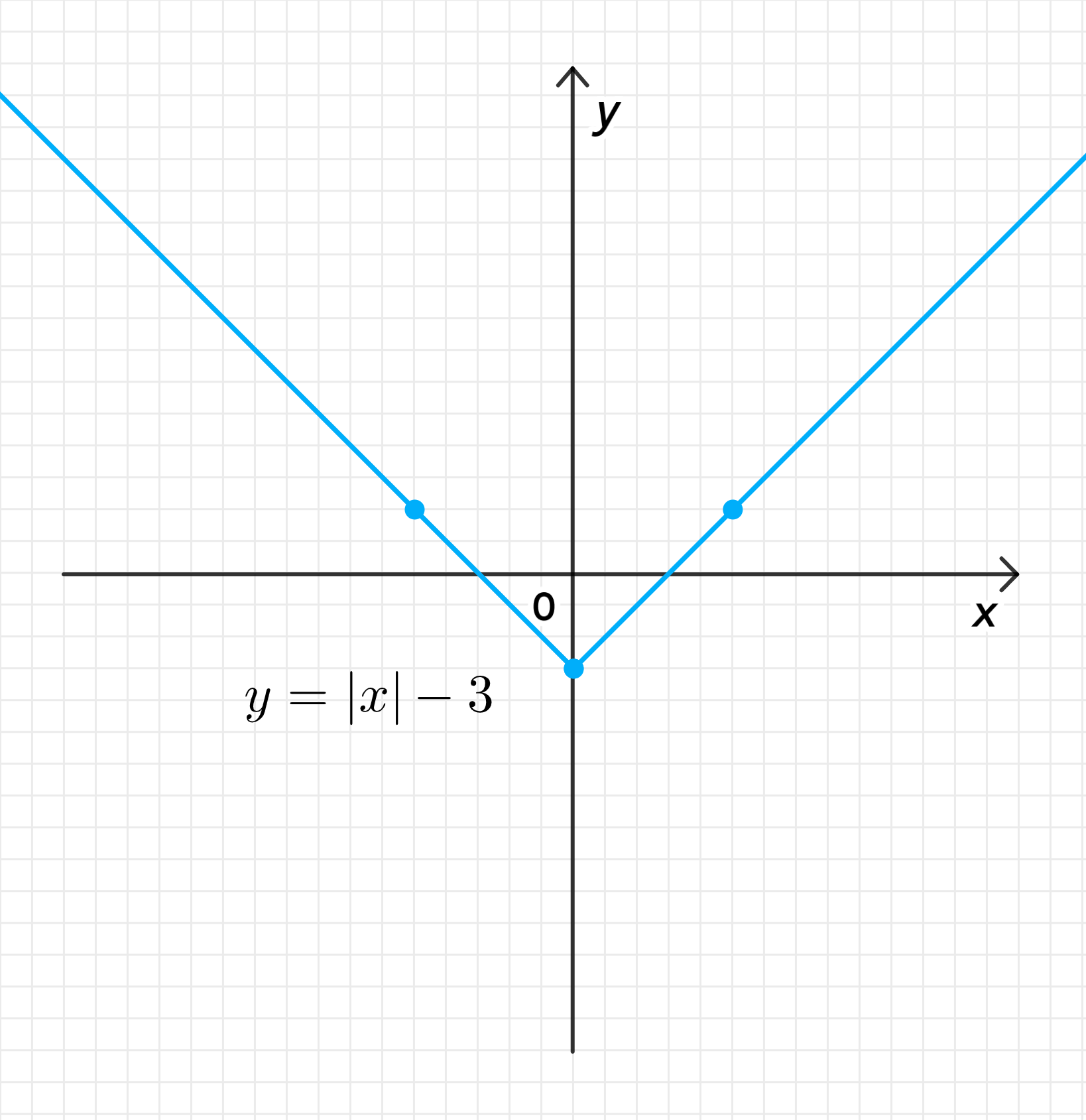
в)
Область определения: ;
Множество значений: ;
Координаты вершины модуля:
и ;
Координаты некоторых точек:
График функции:
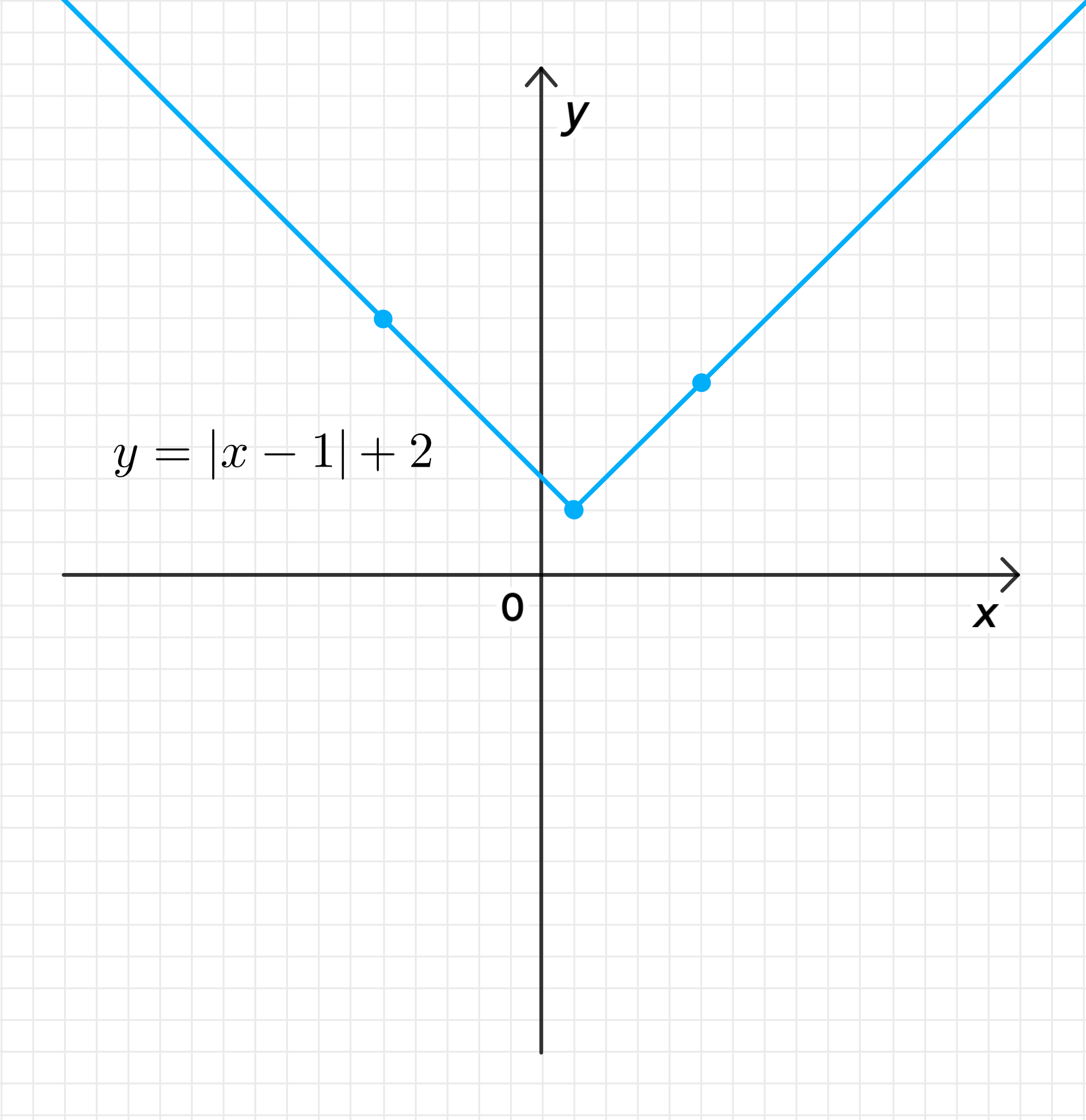
г)
Область определения: ;
Множество значений: ;
Координаты вершины модуля:
и ;
Координаты некоторых точек:
График функции:
а)
1. Область определения:
- Функция определена для всех действительных чисел. Модуль числа всегда существует, независимо от того, является ли положительным или отрицательным.
- Область определения: .
2. Множество значений:
- Модуль числа всегда неотрицателен, так как он выражает расстояние от точки до нуля на числовой оси. Поэтому:
- .
3. Координаты вершины:
- Вершина функции — это точка, где значение функции минимально. Поскольку модуль числа принимает минимальное значение при , то:
- и .
- Вершина функции находится в начале координат .
4. Координаты некоторых точек:
- Чтобы найти другие точки, подставим несколько значений для :
- При , .
- При , .
- При , .
- Таким образом, получаем следующие точки:
5. График функции:
- График функции представляет собой «V»-образную линию, которая симметрична относительно оси . Он имеет вершину в точке , и для значений меньше нуля линия идет вверх вправо, а для значений больше нуля — вверх влево.
б)
1. Область определения:
- Модуль числа всегда существует для любых значений , так что область определения:
- .
2. Множество значений:
- Поскольку модуль всегда неотрицателен, то:
- .
3. Координаты вершины:
- Вершина функции — это точка, в которой значение функции минимально. Модуль достигает минимального значения, когда его аргумент равен нулю. В данном случае аргумент модуля — это , который будет равен нулю при .
- Таким образом, вершина функции: , .
- Вершина функции находится в точке .
4. Координаты некоторых точек:
- Подставим несколько значений :
- При , .
- При , .
- При , .
- Таким образом, получаем следующие точки:
5. График функции:
- График функции представляет собой «V»-образную линию с вершиной в точке , направленную вверх. Он симметричен относительно вертикальной прямой .
в)
1. Область определения:
- Функция по-прежнему определена для всех действительных чисел, так как это модуль. Следовательно:
- .
2. Множество значений:
- Поскольку модуль всегда неотрицателен, минимальное значение будет равно (если , то ). Таким образом:
- .
3. Координаты вершины:
- Вершина функции достигается при , так как модуль минимален при . Подставив , получаем:
- .
- Вершина функции: .
4. Координаты некоторых точек:
- Подставим несколько значений :
- При , .
- При , .
- При , .
- Таким образом, получаем следующие точки:
5. График функции:
- График функции — это «V»-образная линия, с вершиной в точке , направленная вверх. Она симметрична относительно оси .
г)
1. Область определения:
- Модуль функции всегда существует, следовательно:
- .
2. Множество значений:
- Минимальное значение функции достигается при , так как в этом случае , и тогда . Таким образом:
- .
3. Координаты вершины:
- Вершина функции — это точка, где , так как в этой точке выражение равно нулю.
- Вершина функции: .
4. Координаты некоторых точек:
- Подставим несколько значений :
- При , .
- При , .
- При , .
- Таким образом, получаем следующие точки:
5. График функции:
- График функции представляет собой «V»-образную линию с вершиной в точке . Он симметричен относительно вертикальной прямой .