Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.57 Профильный Уровень Мордкович — Подробные Ответы
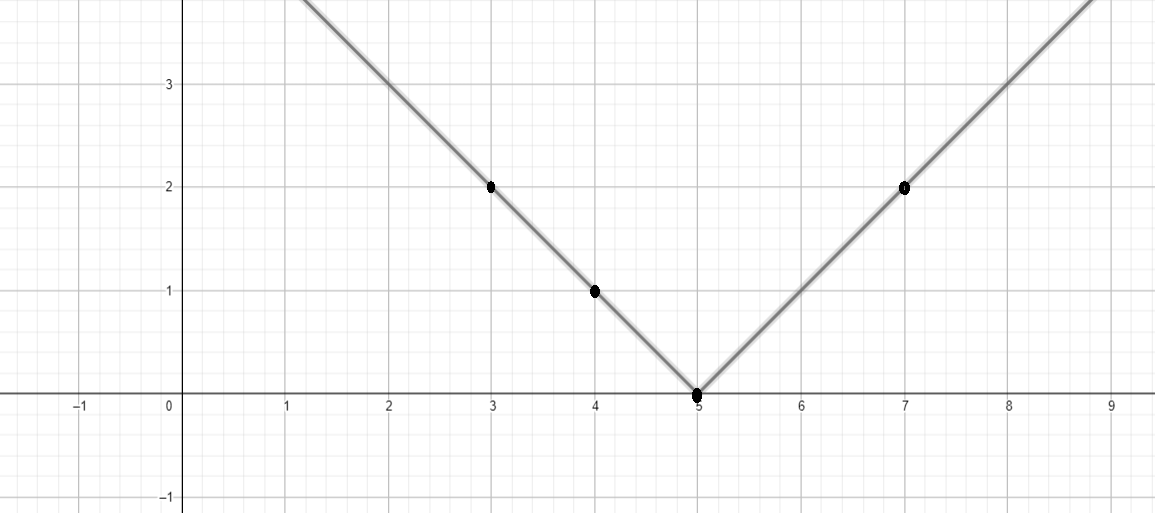
a)
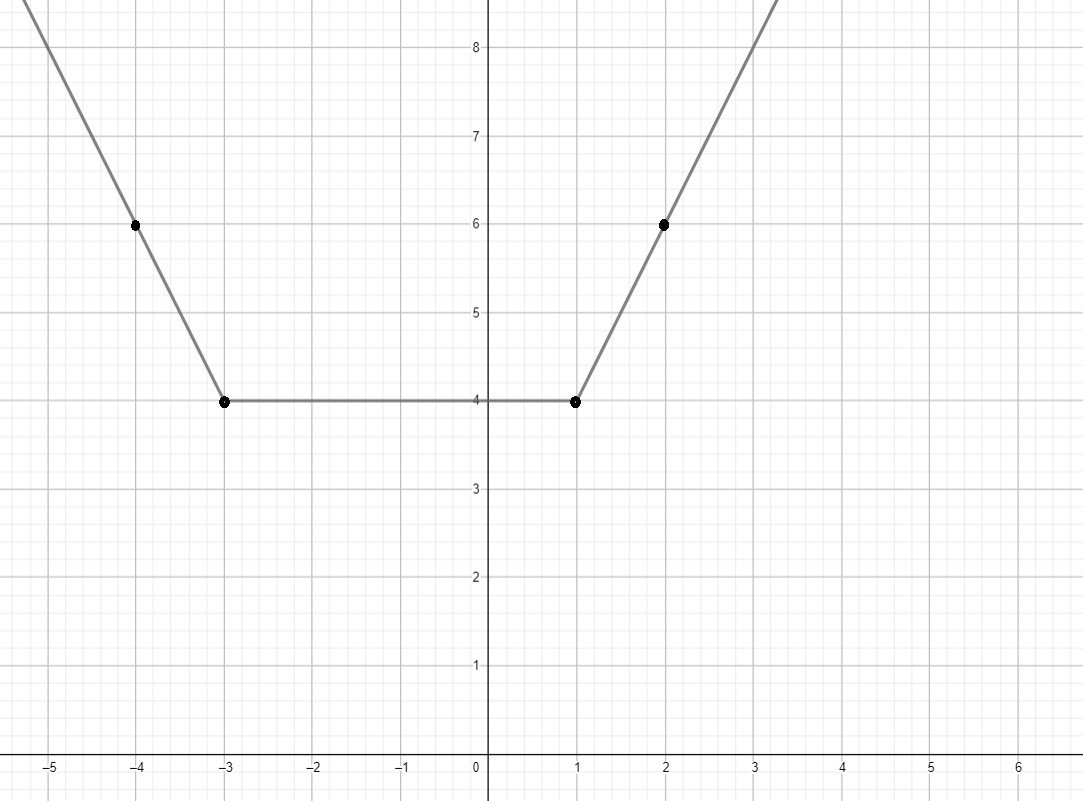
б)
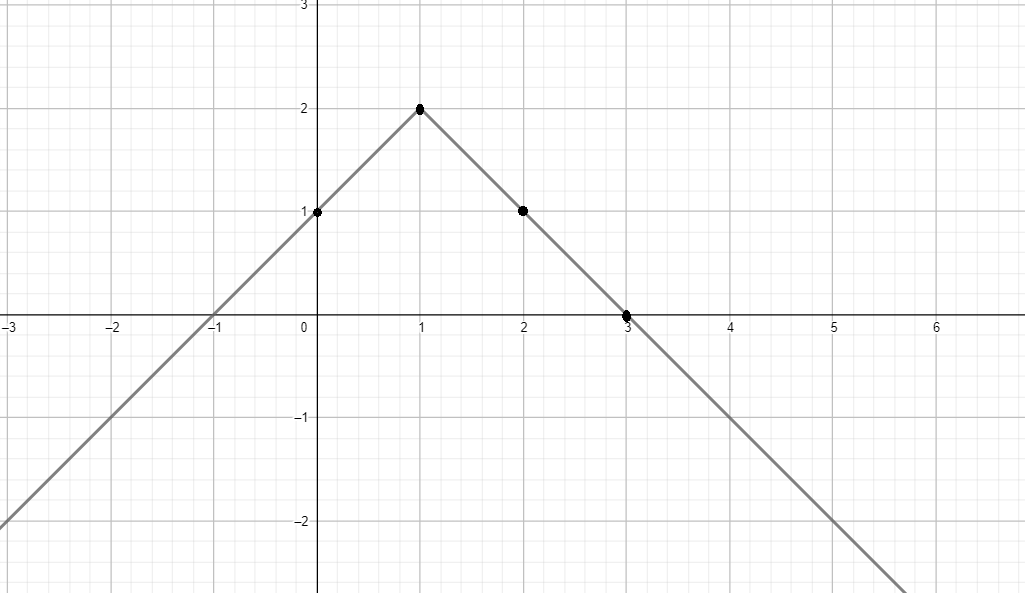
в)
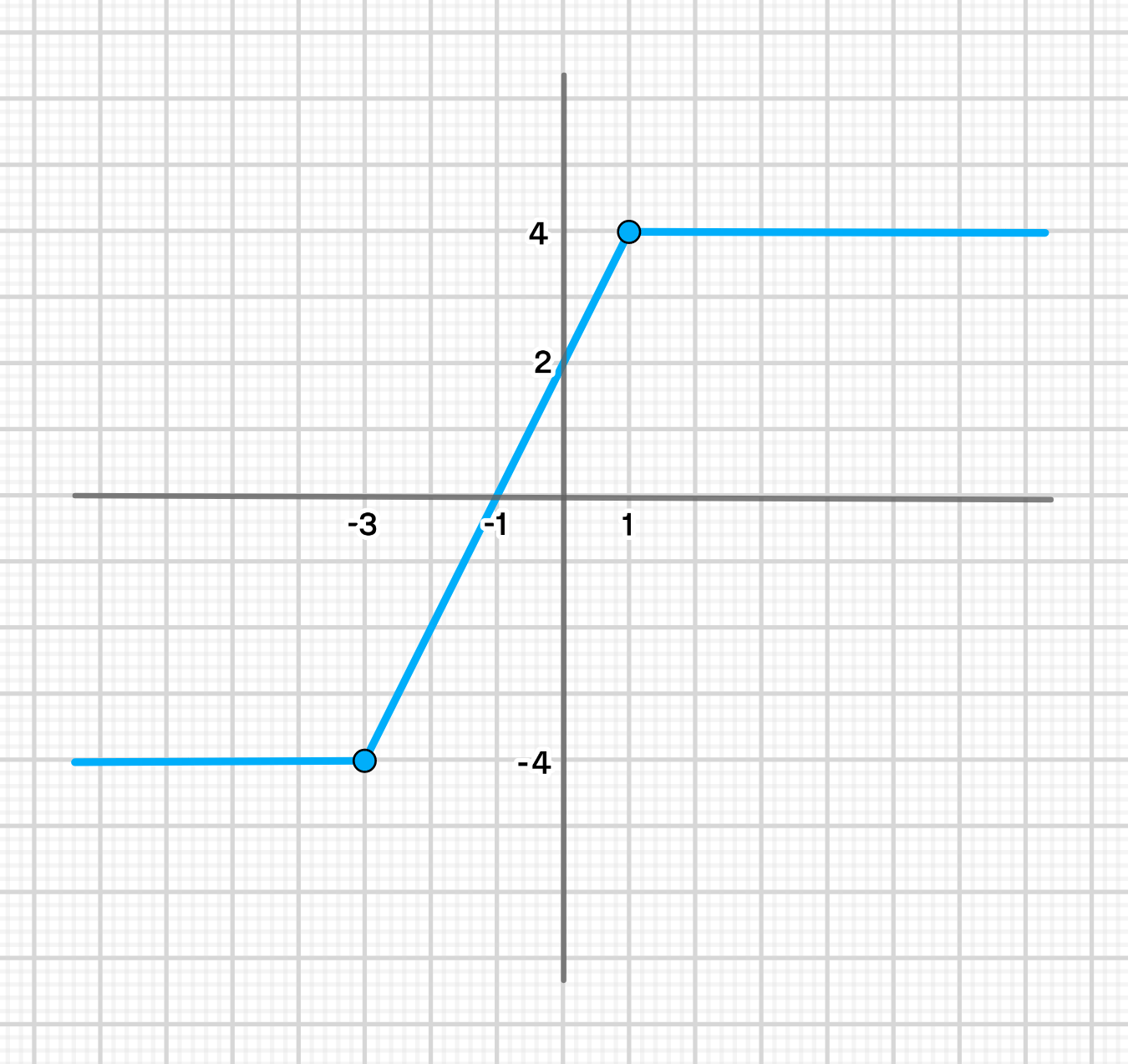
г)
a)
Выражение под знаком модуля:
Если , тогда:
Если , тогда:
График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции:
б)
Выражения под знаком модуля:
Если , тогда:
Если , тогда:
Если , тогда:
График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Функция постоянна на
- Нули функции отсутствуют
в)
Выражение под знаком модуля:
Если , тогда:
Если , тогда:
График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции:
г)
Выражения под знаком модуля:
Если , тогда:
Если , тогда:
Если , тогда:
График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция не убывает
- Функция постоянна на
- Нули функции:
a)
1) Выражение под знаком модуля:
Для функции выражение под знаком модуля — это . Нам нужно рассмотреть два случая:
1.1) Если :
Когда , выражение не меняет знак, и модуль можно опустить, так как значение остается положительным или равным нулю. Тогда .
1.2) Если :
Когда , выражение отрицательно. Модуль переводит его в положительное значение, поэтому:
2) Если , тогда:
- Это линейная функция с угловым коэффициентом 1. Значение при будет равно 0.
Таблица значений функции:
3) Если , тогда:
- Это тоже линейная функция, но с угловым коэффициентом -1. Значение при снова равно 0.
Таблица значений функции:
4) График функции:
- Область определения: , так как функция определена для всех .
- Множество значений: , так как модуль всегда неотрицателен.
- Функция возрастает на : Это происходит потому, что — линейная функция с положительным угловым коэффициентом.
- Функция убывает на : Это происходит потому, что — линейная функция с отрицательным угловым коэффициентом.
- Нули функции: , так как при .
б)
1) Выражения под знаком модуля:
Для функции рассматривали два выражения:
1.1) ⇒:
Для значений выражение будет неотрицательным, и модуль можно опустить.
1.2) ⇒ :
Для значений выражение будет неотрицательным, и модуль тоже можно опустить.
2) Если , тогда:
В этом случае оба модуля раскрываются следующим образом:
Таблица значений функции:
3) Если , тогда:
В этом интервале выражение будет равно , а — равен . Таким образом, функция становится:
Это постоянная функция, и на всем интервале .
4) Если , тогда:
Для значений оба выражения под модулями становятся отрицательными. Модули раскрываются как:
Таблица значений функции:
5) График функции:
- Область определения: , так как функция определена для всех значений .
- Множество значений: , так как минимальное значение функции равно 4, а функция растет для больших значений .
- Функция возрастает на : Это линейная функция , которая возрастает.
- Функция убывает на : Это линейная функция , которая убывает.
- Функция постоянна на : Это постоянная функция .
- Нули функции отсутствуют. для всех , и для других значений функция не достигает нуля.
в)
1) Выражение под знаком модуля:
Для функции рассматривали следующее выражение под модулем:
1.1) ⇒ :
Для значений выражение будет неотрицательным, и модуль можно опустить.
2) Если , тогда:
В этом случае модуль раскрывается как .
Таблица значений функции:
3) Если , тогда:
Когда , выражение становится отрицательным, и модуль раскрывается как:
Таблица значений функции:
4) График функции:
- Область определения: , так как функция определена для всех .
- Множество значений: , так как наибольшее значение функции равно 2, а функция убывает для .
- Функция возрастает на : Это линейная функция , которая возрастает.
- Функция убывает на : Это линейная функция , которая убывает.
- Нули функции: при и .
г)
1) Выражения под знаком модуля:
Для функции рассматривали два выражения под модулем:
1.1) ⇒ :
Для значений выражение будет неотрицательным, и модуль можно опустить.
1.2) ⇒ :
Для значений выражение будет неотрицательным, и модуль тоже можно опустить.
2) Если , тогда:
В этом случае оба модуля раскрываются следующим образом:
3) Если , тогда:
В этом интервале выражение будет равно , а — равен . Таким образом, функция становится:
Таблица значений функции:
4) Если , тогда:
Для значений оба выражения под модулями становятся отрицательными. Модули раскрываются как:
5) График функции:
- Область определения: , так как функция определена для всех значений .
- Множество значений: , так как минимальное значение функции равно -4, а максимальное — 4.
- Функция возрастает на .
- Функция не убывает.
- Функция постоянна на .
- Нули функции: .