Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.58 Профильный Уровень Мордкович — Подробные Ответы
а)
б)
а)
Выражение под знаком модуля:
Если , тогда:
| 5 | 7 | |
|---|---|---|
| 0 | 20 |
Если , тогда:
| -3 | -1 | 1 | 3 | 5 | |
|---|---|---|---|---|---|
| 0 | 12 | 16 | 12 | 0 |
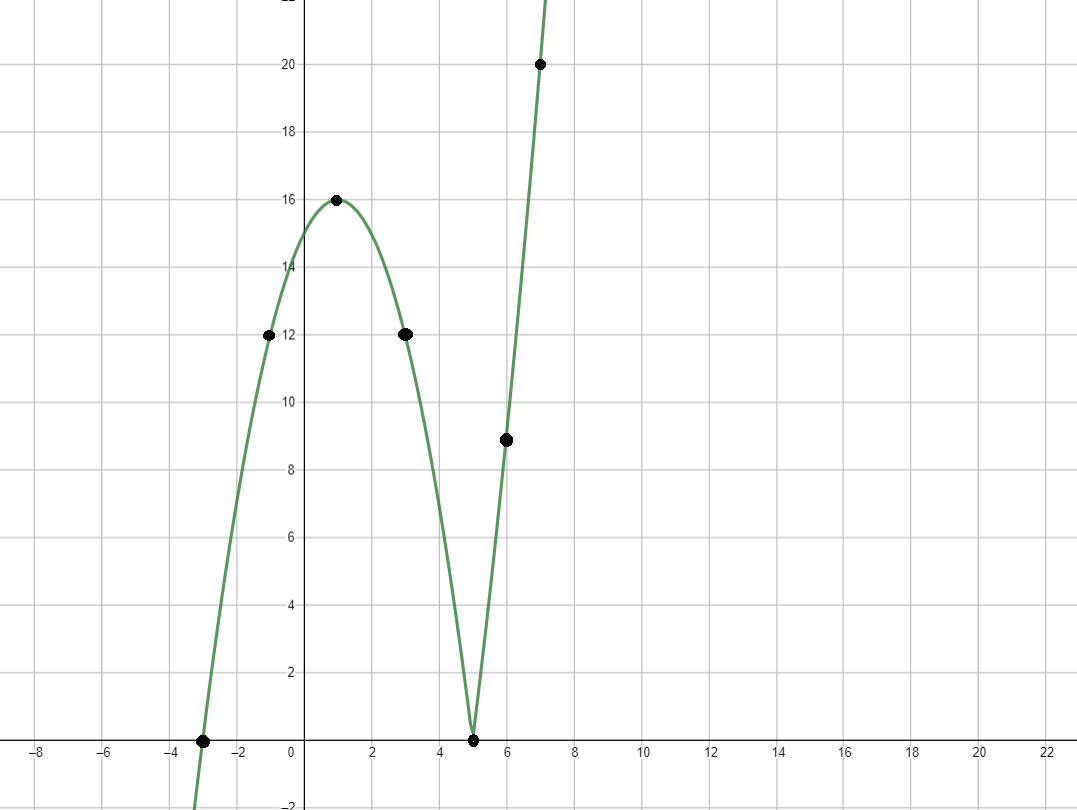
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции: ;
б)
Выражения под знаком модуля:
Если , тогда:
| 1 | 2 | 3 | |
|---|---|---|---|
| 0 | 5 | 12 |
Если , тогда:
| -3 | -2 | -1 | 0 | 1 | |
|---|---|---|---|---|---|
| 0 | 3 | 4 | 3 | 0 |
Если , тогда:
| -5 | -4 | -3 | |
|---|---|---|---|
| 12 | 5 | 0 |
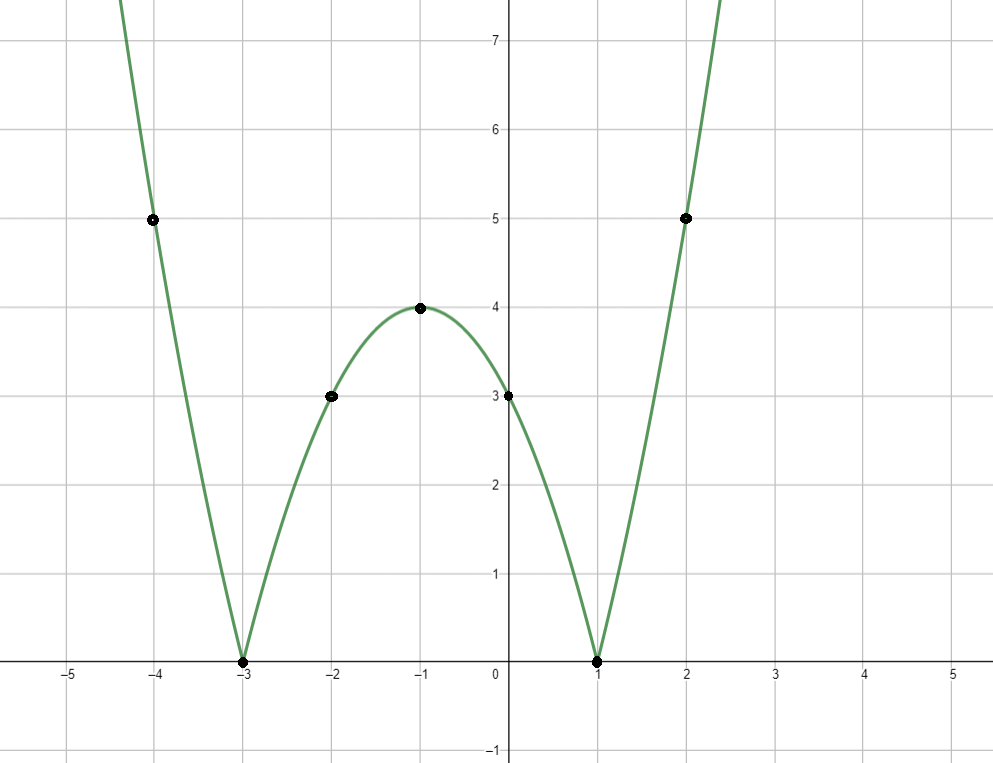
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции:
а)
В данном случае функция состоит из произведения модуля и линейного выражения . Для того чтобы найти поведение функции, нужно рассматривать два случая, так как функция содержит абсолютное значение. Давайте разберем все шаги.
1) Выражение под знаком модуля:
Модуль раскрывается по-разному в зависимости от того, больше ли или меньше 5. Рассмотрим два случая:
- Если : в этом случае выражение , и .
- Если : тогда , и .
2) Если , тогда:
Когда , модуль раскрывается как , и функция будет:
Теперь раскрываем скобки:
Это квадратная функция, для которой можно найти вершину с помощью формулы для абсциссы вершины параболы , где и :
Однако для случая вершина не имеет значения, так как функция для таких значений монотонно возрастает. Находим несколько значений функции, подставив конкретные значения для :
Таблица значений:
| 5 | 7 | |
|---|---|---|
| 0 | 20 |
3) Если , тогда:
Если , модуль раскрывается как , и функция будет:
Теперь раскрываем скобки:
Это также квадратная функция. Чтобы найти вершину, используем ту же формулу для , где и :
Вершина находится на , но мы рассматриваем интервал , следовательно, функция убывает до точки 1 и начинает возрастать после нее. Теперь подставим несколько значений в уравнение, чтобы построить таблицу значений:
Таблица значений:
| -3 | -1 | 1 | 3 | 5 | |
|---|---|---|---|---|---|
| 0 | 12 | 16 | 12 | 0 |
4) График функции:
Теперь, зная, как ведет себя функция для и , можно построить график. График будет состоять из двух частей:
- Для функция возрастает.
- Для функция сначала убывает, а затем возрастает.
- Область определения: (функция определена для всех ).
- Множество значений: (функция может принимать любые значения, как положительные, так и отрицательные).
- Функция возрастает на (на этих интервалах функция возрастает, так как она является параболой с положительным угловым коэффициентом).
- Функция убывает на (на этом интервале функция убывает, так как парабола направлена вниз).
- Нули функции: , .
б)
Для функции также рассмотрим два выражения под модулем:
- зависит от , и раскрывается по-разному:
- Если , то .
- Если , то .
- также зависит от , и раскрывается по-разному:
- Если , то .
- Если , то .
1) Выражения под знаком модуля:
- ;
- ;
2) Если , тогда:
В этом случае оба модуля раскрываются следующим образом:
Вершина параболы находится по формуле:
Таблица значений:
| 1 | 2 | 3 | |
|---|---|---|---|
| 0 | 5 | 12 |
3) Если , тогда:
Здесь выражение для функции будет:
Вершина параболы для этой части:
Таблица значений:
| -3 | -2 | -1 | 0 | 1 | |
|---|---|---|---|---|---|
| 0 | 3 | 4 | 3 | 0 |
4) Если , тогда:
Здесь выражение для функции будет:
Таблица значений:
| -5 | -4 | -3 | |
|---|---|---|---|
| 12 | 5 | 0 |
5) График функции:
- Область определения: .
- Множество значений: .
- Функция возрастает на .
- Функция убывает на .
- Нули функции: , .