Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.59 Профильный Уровень Мордкович — Подробные Ответы
а)
б)
в)
г)
а)
Выражение под знаком модуля:
Выражение имеет смысл при:
Если , тогда:
| 1 | 4 | 5 | |
|---|---|---|---|
| 0 | 1 | 2 |
Если , тогда:
| -11 | -4 | 1 | |
|---|---|---|---|
| 2 | 1 | 0 |
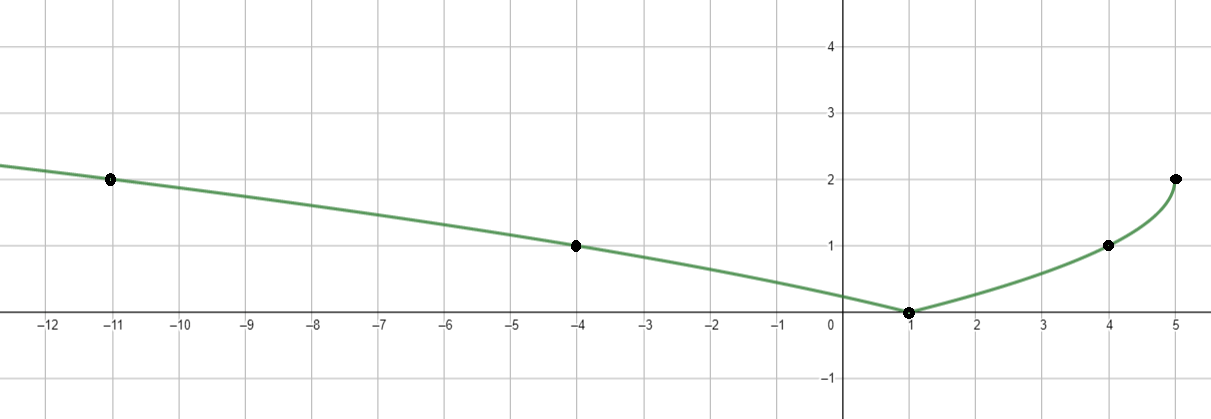
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции: ;
б)
Выражение имеет смысл при:
Если , тогда:
| 0 | 1 | 4 | 5 | |
|---|---|---|---|---|
| -0,2 | 0 | 1 | 2 |
Если , тогда:
| -5 | -4 | -1 | 0 | |
|---|---|---|---|---|
| 2 | 1 | 0 | -0,2 |
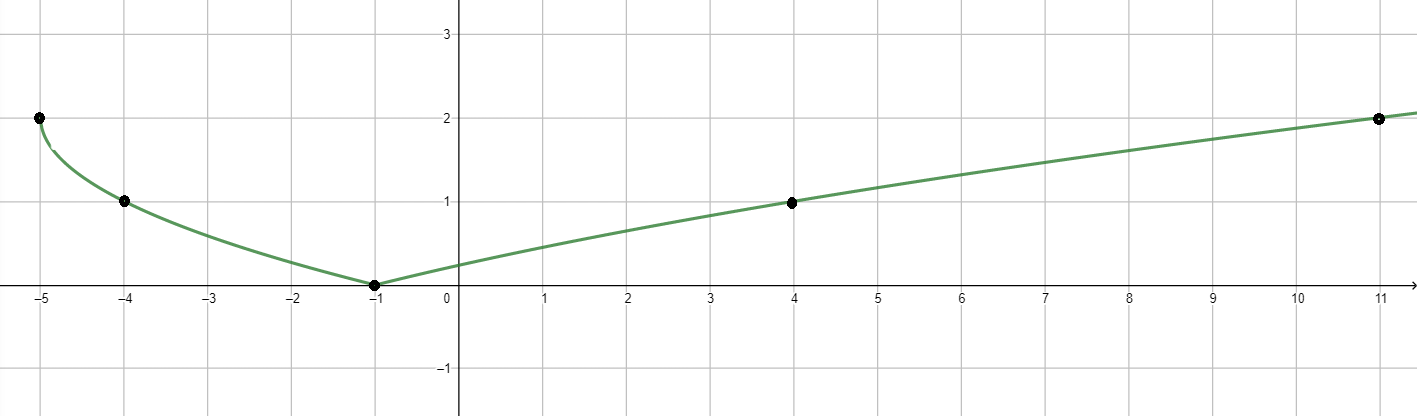
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции: ;
в)
Выражение под знаком модуля:
Выражение имеет смысл при:
Если , тогда:
| -5 | -4 | -1 | |
|---|---|---|---|
| 2 | 1 | 0 |
Если , тогда:
| -1 | 4 | 11 | |
|---|---|---|---|
| 0 | 1 | 2 |
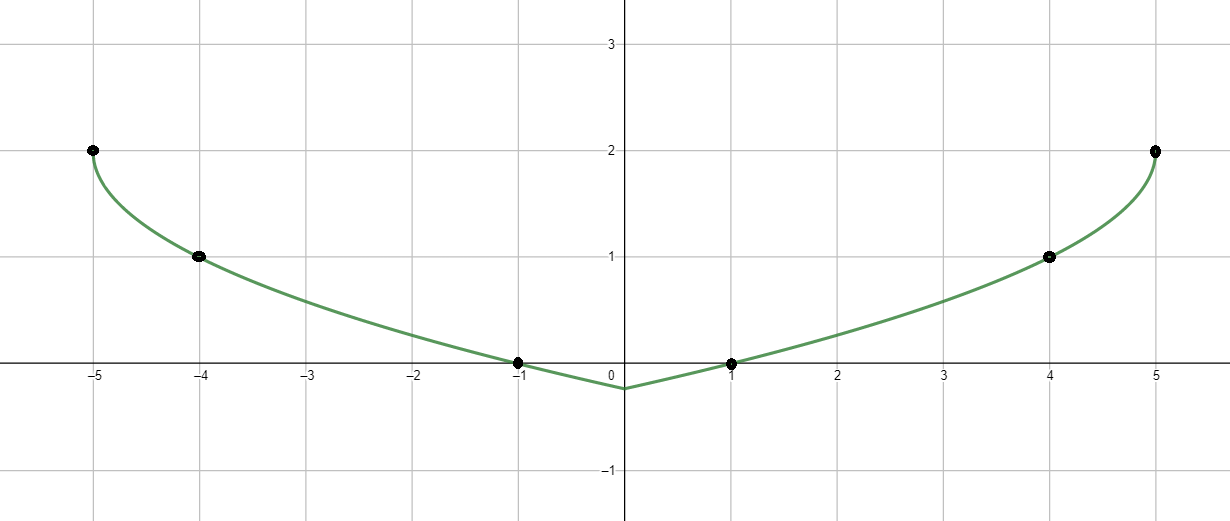
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции: ;
г)
Выражение под знаком модуля:
Выражение имеет смысл при:
Если , тогда:
| 0 | 4 | 11 | |
|---|---|---|---|
| 0,2 | 1 | 2 |
Если , тогда:
| -11 | -4 | 0 | |
|---|---|---|---|
| 2 | 1 | 0,2 |
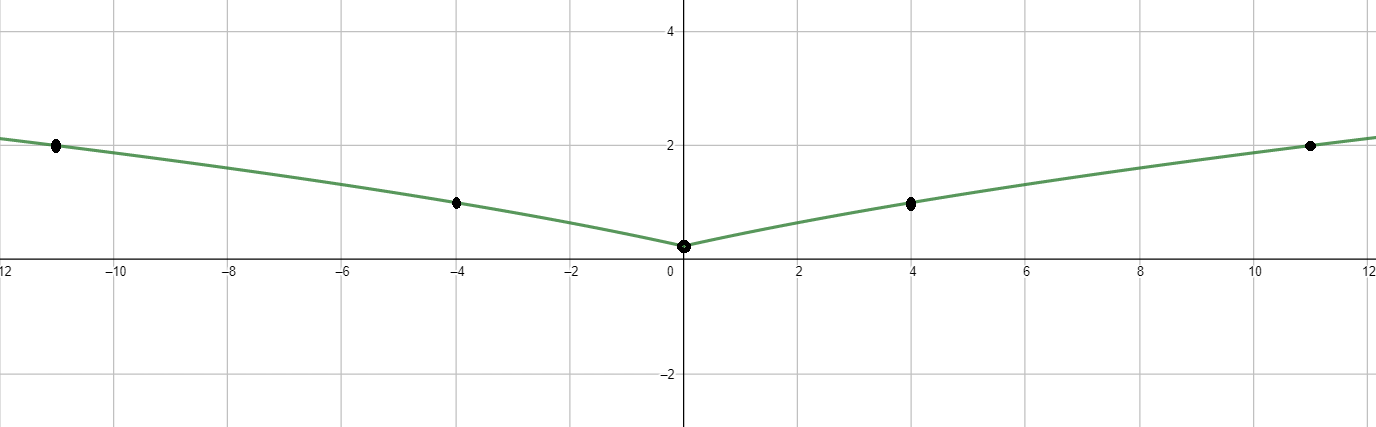
График функции:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на ;
- Функция убывает на ;
- Нули функции отсутствуют
а)
Задача состоит в том, чтобы рассмотреть, при каких значениях выражение внутри модуля и сама функция будут определены, а также изучить поведение функции в различных интервалах.
1) Выражение под знаком модуля:
Модуль требует, чтобы выражение под корнем было неотрицательным, то есть:
Решаем это неравенство:
Также, для того чтобы выражение было неотрицательным, должно выполняться:
Решим это неравенство:
Возводим обе части неравенства в квадрат:
Решаем это неравенство:
Таким образом, для функции существует ограничение:
2) Выражение имеет смысл при:
Условие, что , означает, что . Следовательно, должно лежать в интервале:
Таким образом, область определения функции: .
3) Если , тогда:
Для значений из интервала функция будет:
Рассмотрим поведение функции в пределах этого интервала. Мы подставим несколько значений в уравнение, чтобы изучить результат:
- При :
- При :
- При :
Таким образом, значения функции на интервале составляют: .
Таблица значений функции:
| 1 | 4 | 5 | |
|---|---|---|---|
| 0 | 1 | 2 |
4) Если , тогда:
Если , то выражение под знаком модуля изменится на:
Теперь рассчитаем несколько значений:
- При :
- При :
- При :
Таким образом, значения функции на интервале составляют .
Таблица значений функции:
| -11 | -4 | 1 | |
|---|---|---|---|
| 2 | 1 | 0 |
5) График функции:
Для построения графика функции следует отметить, что:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции:
б)
Задача с абсолютным значением потребует разделения на три случая в зависимости от того, какой знак имеет .
1) Выражение имеет смысл при:
Чтобы корень был определен, нам нужно, чтобы . Решаем это:
Следовательно, область определения функции:
2) Если , тогда:
На интервале , выражение для функции будет:
Посмотрим на поведение функции:
- При :
- При :
- При :
Таблица значений функции:
| 0 | 1 | 4 | 5 | |
|---|---|---|---|---|
| -0.236 | 0 | 1 | 2 |
3) Если , тогда:
Для значений из интервала выражение для функции будет:
Посмотрим, как ведет себя функция:
- При :
- При :
- При :
Таблица значений функции:
| -5 | -4 | -1 | 0 | |
|---|---|---|---|---|
| 2 | 1 | 0 | -0.236 |
4) График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции:
в)
Для этой функции важно рассматривать условие, при котором выражение под корнем и выражение внутри модуля будут определены.
1) Выражение под знаком модуля:
Для выражения нам нужно, чтобы:
Возводим обе части в квадрат:
Решаем это:
2) Выражение имеет смысл при:
Для выражения необходимо, чтобы:
Таким образом, область определения функции:
3) Если , тогда:
На интервале , функция будет:
Посмотрим на поведение функции:
- При :
- При :
- При :
Таблица значений функции:
| -5 | -4 | -1 | |
|---|---|---|---|
| 2 | 1 | 0 |
4) Если , тогда:
Когда , выражение под знаком модуля изменится на:
Посмотрим на поведение функции:
- При :
- При :
- При :
Таблица значений функции:
| -1 | 4 | 11 | |
|---|---|---|---|
| 0 | 1 | 2 |
5) График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции:
г)
Эта функция требует рассматривать абсолютное значение , а также уточнять области определения и поведения функции.
1) Выражение под знаком модуля:
Для выражения :
Возводим обе части в квадрат:
Решаем:
Но поскольку , данное неравенство не имеет решений. Таким образом, функция не определена для таких .
2) Выражение имеет смысл при:
Выражение имеет смысл при:
Это условие выполняется для всех , то есть область определения функции — все действительные числа.
3) Если , тогда:
Для :
Таблица значений:
| 0 | 4 | 11 | |
|---|---|---|---|
| 0,2 | 1 | 2 |
4) Если , тогда:
Для :
Таблица значений:
| -11 | -4 | 0 | |
|---|---|---|---|
| 2 | 1 | 0,2 |
5) График функции:
- Область определения:
- Множество значений:
- Функция возрастает на
- Функция убывает на
- Нули функции отсутствуют