Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 9.5 Мордкович — Подробные Ответы
В координатной плоскости хОу постройте прямую, которая удовлетворяет уравнению: а) 2х — 6 = 0; г) —4х + 1 = 5; б) -3у + 6 = 0; д) 0,5у — 2 = -1; в) 5х = 0; е) —3у = 0.
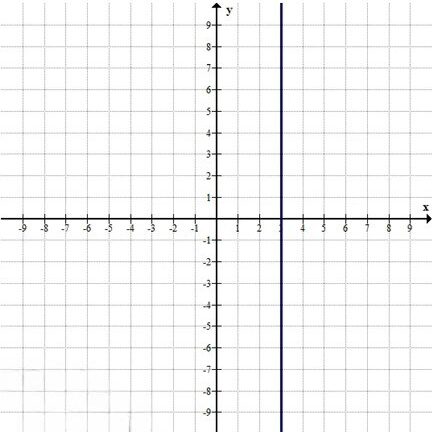
a)
\( 2x — 6 = 0 \)
\( 2x = 6 \)
\( x = 3 \)
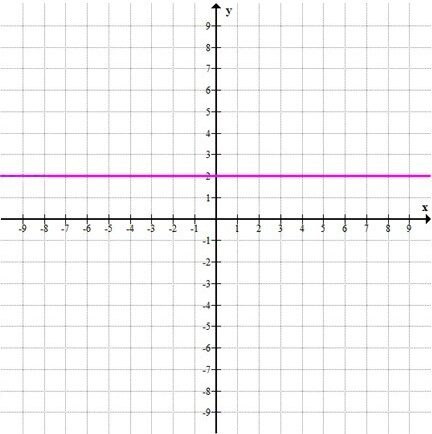
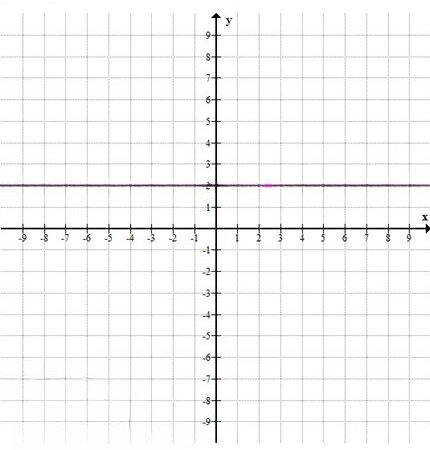
б)
\( -3y + 6 = 0 \)
\( -3y = -6 \)
\( y = 2 \)
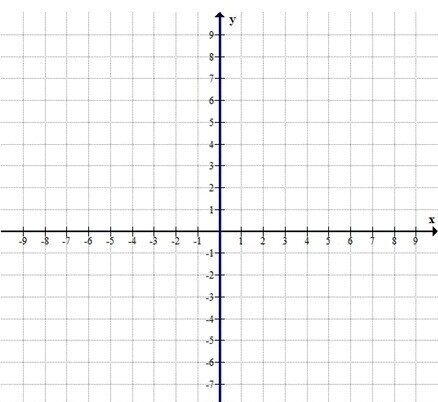
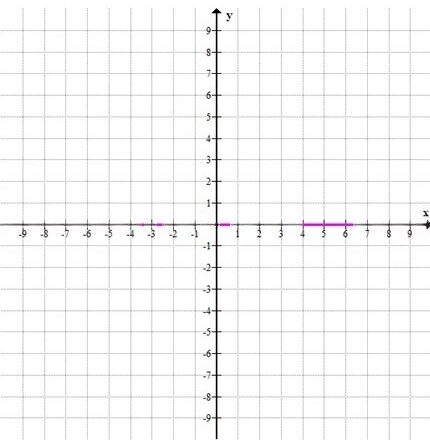
в)
\( 5x = 0 \)
\( x = 0 \)
г)
\( -4x + 1 = 5 \)
\( -4x = 4 \)
\( x = -1 \)
д)
\( 0.5y — 2 = -1 \)
\( 0.5y = 1 \)
\( y = 2 \)
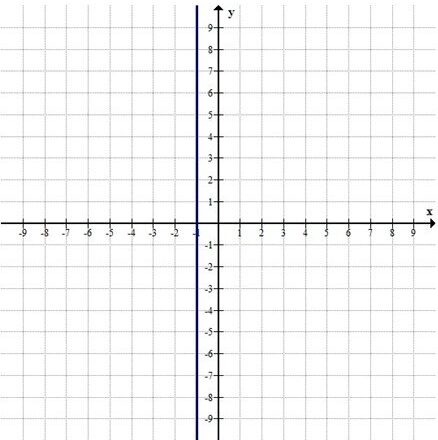
е)
\( -3y = 0 \)
\( y = 0 \)
а)
\( 2x — 6 = 0 \)
Прибавим к обеим частям уравнения число \( 6 \):
\( 2x — 6 + 6 = 0 + 6 \)
Упростим:
\( 2x + 0 = 6 \)
\( 2x = 6 \)
Разделим обе части уравнения на \( 2 \):
\( \frac{2x}{2} = \frac{6}{2} \)
\( x = 3 \)
б)
\( -3y + 6 = 0 \)
Вычтем из обеих частей уравнения число \( 6 \):
\( -3y + 6 — 6 = 0 — 6 \)
Упростим:
\( -3y + 0 = -6 \)
\( -3y = -6 \)
Разделим обе части уравнения на \( -3 \):
\( \frac{-3y}{-3} = \frac{-6}{-3} \)
\( y = 2 \)
в)
\( 5x = 0 \)
Разделим обе части уравнения на \( 5 \):
\( \frac{5x}{5} = \frac{0}{5} \)
\( x = 0 \)
г)
\( -4x + 1 = 5 \)
Вычтем из обеих частей уравнения число \( 1 \):
\( -4x + 1 — 1 = 5 — 1 \)
Упростим:
\( -4x + 0 = 4 \)
\( -4x = 4 \)
Разделим обе части уравнения на \( -4 \):
\( \frac{-4x}{-4} = \frac{4}{-4} \)
\( x = -1 \)
д)
\( 0{,}5y — 2 = -1 \)
Прибавим к обеим частям уравнения число \( 2 \):
\( 0{,}5y — 2 + 2 = -1 + 2 \)
Упростим:
\( 0{,}5y + 0 = 1 \)
\( 0{,}5y = 1 \)
Разделим обе части уравнения на \( 0{,}5 \):
\( \frac{0{,}5y}{0{,}5} = \frac{1}{0{,}5} \)
\( y = 2 \)
е)
\( -3y = 0 \)
Разделим обе части уравнения на \( -3 \):
\( \frac{-3y}{-3} = \frac{0}{-3} \)
\( y = 0 \)